Измерение горизонтальных углов способом всевозможных комбинаций

Способ всевозможных комбинаций (СВК) предложил Гаусс. Позднее он был усовершенствован Шрейбером. Данный способ применяется при измерении углов в триангуляции и полигонометрии 1 и 2 классов, а также в специальных геодезических сетях повышенной точности.

Суть этого способа заключается в следующем.

n

А

Рис. 8.1. Пояснения к способу всевозможных комбинаций

1,2,3,4...n — номера наблюдаемых направлений.

Пусть на пункте А нам необходимо отнаблюдать n направлений (1,2,3,4...n). Согласно рассматриваемому способу мы должны на пункте измерить все возможные комбинации углов, образуемые парными сочетаниями всех направлений .
Число углов r , измеряемых в СВК, можно вычислить по формуле (8.2).

(8.2)

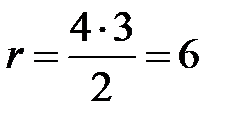Так при n =5 углов, при n =4 углов.

Вес уравненных на станции направлений в способе всевозможных комбинаций вычисляют по формуле:

(8.3)

где n – число направлений; m – число приемов.

(8.4)

С целью соблюдения условия равноточности результатов измерений на пунктах одного класса, обеспечения независимости измерений углов и ослабления влияния ошибок диаметров лимба Шрейбер поставил в основу способа два требования:

1. (для всех пунктов сети одного класса).Так в триангуляции 1-ого класса = 35 – 36, в триангуляции 2 класса Р = 21 – 25. При наблюдениях со сложных сигналов вес Р увеличивается на 25 – 30%.

2. Каждое направление необходимо измерять при одном и том же положении лимба по возможности только один раз.

Выполнение второго требования достигается двойной перестановкой лимба:

а) перестановкой лимба между приемами на угол

или , (8.5)

где m – число приемов, i –цена деления лимба.

б) перестановкой лимба при переходе к измерению следующего угла на величину

или (если n – четное) (8.6)

или (если n – нечетное) (8.7)

Рассчитаем таблицу установок лимба для теодолита ОТ-02 для n = 4,

, i =4' (таблица 8.1). В этом случае ,

а .

Таблица 8.1

Расчетные установки лимба

n = 4 m = 6

№ приема   Назв. угла
1.2 1.3 1.4	0°00¢ 10°04¢ 20°08¢	30°04¢ 40°08¢ 50°12¢	60°08¢ 70°12¢ 80°16¢	90°12¢ 100°16¢ 110°20¢	120°16¢ 130°20¢ 140°24¢	150°20¢ 160°24¢ 170°28¢
2.3 2.4 3.4	20°08¢ 10°04¢ 0°00¢	50°12¢ 40°08¢ 30°04¢	80°16¢ 70°12¢ 60°08¢	110°20¢ 100°16¢ 90°12¢	140°24¢ 130°20¢ 120°16¢	170°28¢ 160°24¢ 150°20¢

Таблица расчетных установок лимба может быть взята готовой из инструкции. Однако на пункте угловые наблюдения выполняют не по расчетным установкам лимба, а по рабочим, которые получают по следующему правилу:

Для углов, связанных с первым (начальным) направлением (1.i), рабочие установки лимба совпадают в точности с теми, что даны в таблице расчетных установок лимба; для углов, не связанных с первым направлением (2.3, 2.4, 3.4 и т.д.), рабочую установку лимба получают прибавлением к расчетной установке угла 1. j , где j –номер левого направления угла. Т.е. при расчете рабочих установок для углов 2.3 и 2.4 прибавляют предварительно измеренный с точностью до минуты угол 1.2; для угла 3.4 – угол 1.3 и т. д.

Согласно сформулированному правилу составим таблицу рабочих установок лимба на основании таблицы 8.1, приняв измеренный угол 1.2 = 14^о 08' , а угол 1.3 = 25^о 12' (таблица 8.2).

Таблица 8.2

Рабочие установки лимба ( n = 4; m = 6)

№ приема   Назв. угла
1.2 1.3 1.4	0°00¢ 10°04¢ 20°08¢	30°04¢ 40°08¢ 50°12¢	60°08¢ 70°12¢ 80°16¢	90°12¢ 100°16¢ 110°20¢	120°16¢ 130°20¢ 140°24¢	150°20¢ 160°24¢ 170°28¢
2.3 2.4 3.4	34°16¢ 24°12¢ 25°12¢	64°20¢ 54°16¢ 55°16¢	94°24¢ 84°20¢ 85°20¢	124°28¢ 114°24¢ 115°24¢	154°32¢ 144°28¢ 145°28¢	184°36¢ 174°32¢ 175°32¢

Методика измерения отдельного угла в приеме

Пользуясь таблицей рабочих установок лимба, на горизонтальном круге устанавливают необходимый отсчет. Затем наводят биссектор трубы на левый предмет, т.е. А, и берут отсчет . Вращая по ходу часовой стрелки, на правое направление В и берут отсчет ( первый полуприем).

А

В

A.B

360-А.B

Рис. 8.2. Измерение угла в СВК

 

Далее приступают к выполнению второго полуприема. Для чего переводят трубу через зенит и, вращая алидаду по ходу часовой стрелки, вновь наводят на правый предмет, т.е. В, и берут отсчет . Затем вращением алидады по ходу часовой стрелки наводят трубу на левый предмет и берут последний отсчет .

(8.8)

Таким образом, в первом полуприеме измеряют угол А.В, а во втором – его дополнение до 360^о, т.е. (360^о— А.В) (рис.8.2).

Данная программа наблюдений является оптимальной, т.к. она позволяет уменьшить влияния кручения знака и азимутального смещения лимба на результаты угловых измерений, что легко прослеживается из следующих рассуждений.

Обозначим через j₁ и j₂ - влияние кручения знака соответственно в 1-ом и 2-ом полуприемах, а через l₁и l₂– влияние азимутального смещения лимба в 1-ом и 2-ом полуприемах.

Если в схеме (8.8) через , , , принять истинные отсчеты по горизонтальному кругу, то фактические отчеты с учетом влияний рассматриваемых погрешностей по данной методике будут следующие:

Наблюдаемые пункты	Фактические отсчеты по горизонтальному кругу
1-ый полуприем	2-ой полуприем
А   В
Искомый угол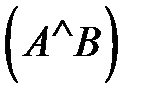

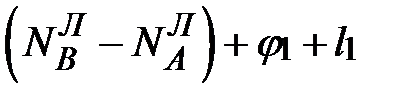
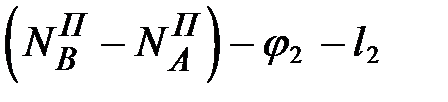
(8.9)

Так как продолжительность полуприемов примерно одинакова, то и . Поэтому в (8.9) разности с j и l при наблюдении по данной методике должны скомпенсироваться или по крайней мере заметно уменьшиться. Следовательно, принятая методика наблюдений углов в способе всевозможных комбинаций является оптимальной.

Полевые контроли в способе всевозможных комбинаций

1. Значения углов, вычисленные в полуприемах (КЛ и КП) не должны различаться более, чем на 8². (В сущности – это допуск на колебание коллимации в приеме).

2. Расхождения между значениями одного и того же угла в различных приемах не должны превышать: 1кл.- 4²; 2кл. - 5².

Если данный допуск не выдержан, то угол перенаблюдается на установках, соответствующих его min и max значениям. Число перенаблюденных углов в программе не должно превышать 30% от общего количества углов.

3. Колебания средних значений одного и того же угла, полученных как по непосредственному его измерению, так и по вычислению в виде суммы или разности двух других углов, не должны превышать 3² при числе направлений 5 и 4² при n > 5.

На производстве в связи с этим допуском существует термин; «комбинации разлетелись». Если данный допуск не выдержан, т.е. «комбинации разлетелись», программа наблюдений на пункте повторяется заново.

8.2. Уравнивание на станции результатов измерений в способе всевозможных комбинаций

хn-1

х3

х2

х1

А

n

Уравнивание на станции результатов измерений в рассматриваемом способе выполняется по СНК параметрическим методом. В качестве необходимых неизвестных здесь выбираются углы, связанные с начальным направлением (рис. 8.3).

Рис. 8.3. Иллюстрация к уравниванию на станции в СВК

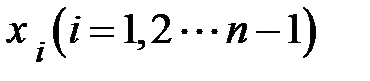- углы, связанные с начальным направлением, выбранные в качестве необходимых неизвестных.

Схема уравнивания по СНК:

а) Составление уравнений поправок.

(8.10)

…………….

………………

………………….

…………………….

…………………..

…………………..

б) Сведем все уравнения поправок в таблицу

…   (n—1)	(n—1)x1 — x2 — x3 —… xn—2 — xn— 1 – 1.2 + 2.3 + 2.4 +…+ 2.n = 0 -x1 + (n—1) x2 - x3 -…- xn—2 -xn— 1 —1.3 – 2.3 + 3.4 + … + 3.n = 0 -x1 - x2 +(n—1) x3 -… -xn—2 - xn-1 – 1.4 – 2.4 – 3.4 + 4.5 +…+4.n = 0 … … … … … … … … … … … … … (8.11) -x1 -x2 - x3 - …+(n-1)xn-2 - xn- 1 – 1.(.n-1) - 2.(n-1) - 3.(n-1) - +( n -1).n = 0 -x1 - x2 -x3 - … - xn-2 + (n-1)xn-1 - 1.n - 2.n - 3.n- … - (n -1).n = 0
å	x1 + x2 + x3 + … +xn-2 + xn-1 – 1.2 – 1.3 -…-1.n = 0

г) Определение неизвестных x_i :

Для определения неизвестных получаем суммарное уравнение å, а затем последовательно складываем каждое из входящих в систему (8.11) уравнение с суммарным, получая:

— Уравнение 1 + ∑

n^. x₁ = 2^. 1.2 + (1.3 – 2.3) + (1.4 – 2.4)+…… +(1.n – 2.n)

Отсюда

x₁ = [1.2]_ур.=( 2^. 1.2 + (1.3 – 2.3) + (1.4 – 2.4)+…… +(1.n – 2.n))/ n

— Уравнение 2 + ∑ (8.12)

x₂ = [1.3]_р.= (2^. 1.3 + (1.2+ 2.3) + (1.4 – 3.4)+…… +(1.n – 3.n))/ n

— Уравнение (n—1) + ∑

x_n—1 = [1.n]_р.= (2^. 1.n + (1.2 + 2.n) + (1.3 + 3.n)+…… +(1.(n –1)+ (n—1).n))/ n

В (8.12) через [1.2]_ур., [1.3]_ур. ,….. [1.n]_ур. обозначены уравненные значения углов на станции, связанные с начальным направлением.

Из формулы (8.12) следует, что любой уравненный угол [1.j]_ур. определяется как среднее весовое из всех имеющихся углов (измеренного и вычисленных из комбинаций): при этом непосредственно измеренному углу приписывают вес, равный 2, а всем остальным значениям его, найденным из комбинаций соответствующих пар измеренных углов, приписывают вес, равный 1.

Любой уравненный угол [k.j]_ур (k 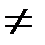1)определяют из формулы:

[k.j]_ур = [1.j]_ур — [1.k]_ур

Кроме того, любой уравненный угол [k.j]_ур можно определить согласно сформулированному правилу для [1.j]_ур.

Пример: n=4. Измеряемые углы: 1.2 1.3 1.4

2.3 2.4

3.4

[1.2]_ур. ={ 2[1.2]_изм.+(1.3-2.3)+(1.4 – 2.4)}/4