Резистивный заряд емкостных накопителей

Резистивный заряд емкостных накопителей несмотря на обычно низкий КПД (h = 0,5 в режиме полного разряда) достаточно широко применяется на практике в силу своей простоты и надежности. Обычно такой заряд используется в установках, имеющих малую среднюю мощность при низкой частоте следования импульсов тока нагрузки. Помимо этого резистивный заряд может быть использован при существенных значениях сред­ней мощности импульсных установок, если накопитель работает в режиме частичного разряда. В данном случае удается получить значения КПД более 90 % при разряде накопителя за время формирования импульса не более чем на 20 % от предразрядного напряжения. Определенным недостатком такого решения является необходимость применения в цепи разряда силовых полностью управляемых ключей, что несколько снижает надежность импульсного генератора в целом, но позволяет получать в нагрузке импульсы регулируемой частоты и регулируемой длительности только за счет изменения режимов работы полностью управляемого ключа.

На рис. 6.1 приведена простейшая схема генератора с резистивным зарядом емкостного накопителя, а на рис. 6.2 – временные зависимости тока заряда и напряжения на емкостном накопителе.

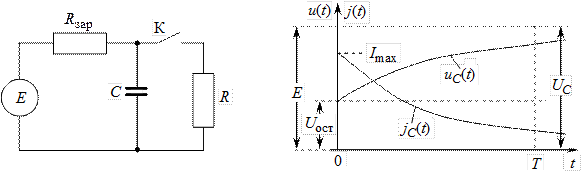
Рис. 6.1 Рис. 6.2

Аналитические расчеты КПД резистивного заряда обычно содержат экспоненциальные члены и учитывают временные интервалы процесса заряда, что усложняет инженерный расчет и не поясняет физическую сторону энергетики процессов резистивного заряда [2], [7].

В тех случаях, когда зарядный резисторявляется нелинейным, т. е. Rзар = f(i), или сопротивление резистора меняется в силу каких-либо причин во времени, т. е. Rзар = f(t), выбор токоограничивающего сопротивления, расчет его средней мощности и определение КПД в каждом конкретном случае становятся затруднительными.

Для того чтобы избежать сложных расчетов и одновременно получить точное значение КПД процесса резистивного заряда для произвольных зависимостей вида Rзар =const, Rзар = f(t) или Rзар = f(i), сформулируем и докажем следующую теорему.

Теорема 1. КПД процесса резистивного заряда емкостного накопителя от источника постоянного напряжения E = const инвариантен относительно каких-либо изменений значения сопротивления резистора в процессе заряда, не зависит от значения емкостного накопителя и времени заряда, а определяется только уровнями напряжения заряда UСи остаточного напряжения Uост.

Требуемое значение предразрядного напряжения UСопределяется нагрузкой емкостного накопителя, а значение Uост– параметрами контура разряда и (или) режимом работы выходного ключа.

В этом случае заряд, приобретенный накопителем,

q = C(UС– Uост),

причем накопитель в процессе разряда может и перезаряжаться, что учитывается знаком Uост, т. е. при неполном разряде накопителя напряжение Uостположительно, а при перезаряде – отрицательно.

Энергия, потребленная от источника ЭДС в процессе заряда,

WЕ = qE == CE(UС– Uост).

Энергия, выделенная в разрядном контуре,

Wн = ,

Определим КПД как

h = Wн/WЕ = CE(UС– Uост) = (UС + Uост)/2E. (6.1)

Введем значения коэффициента заряда bзар = UС/E и коэффициента остаточного напряжения bост = Uост/E.

Тогда

h = (bзар + bост)/2. (6.2)

Зависимости (6.1) или (6.2) являются доказательством теоремы, поскольку ни значение зарядного резистора и его вольт-амперная характеристика, ни временные параметры и значение величины емкостного накопителя здесь не фигурируют, а КПД определяется только его предразрядным и остаточным напряжениями.

Зависимость (6.2) в случае полного разряда накопителя дает значение КПД h = 0,5 при условии UС = E. На рис. 6.3 приведены графические зависимости для h = f(bзар) различных значений bостс учетом того, что всегда

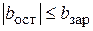. (6.3)

Точка (h = 1,0; bзар = 1,0) определяет отсутствие разряда, а точка (h = 0; bзар = 0) – отсутствие заряда, что объясняется предельным переходом от значений bзар < 1 к значению bзар = 1 и от значений bзар > 0 к значению bзар = 0.

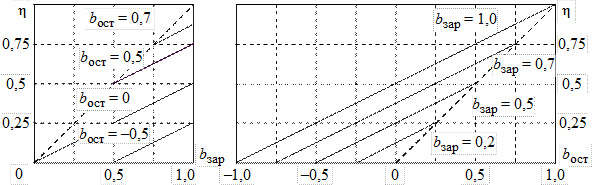
Рис. 6.3 Рис. 6.4

На рис. 6.4 приведены зависимости h = f(bост) для различных значений bзарс учетом (6.3). Из рисунка наглядно видно, что использование зарядного источника, выходное напряжение которого существенно превышает максимальное напряжение заряда, т. е. E > UС max, приводит к существенному снижению КПД процесса заряда. В тех случаях, когда энергия накопителя в нагрузке не выделяется, КПД равен либо 1,0 (bост = + 1), либо 0 (bост = –1), что достаточно тривиально, но тем не менее хорошо иллюстрирует энергетику процесса и определяет два предельных значения КПД в предельных режимах работы разрядного контура. Поскольку для резистивного заряда Rзар = const уровень UСдостигает значения E только за время t = ¥, может возникнуть сомнение в точности оценки КПД. При выполнении условия Tзар = 3RзарС уровень UС = 0,95E, а при Tзар = 5RзарС уровень UС = 0,993E, т. е. точность оценки значения UСпревышает 5 %, что вполне достаточно для инженерных расчетов. В случае, когда Rзар = f(t) или Rзар = f(i), необходимо выбрать максимальное значение зарядного резистора Rmaxиз условия Rmax £ Tзар/(3...5)C, что гарантированно обеспечит процесс заряда до значений UС » E в заданном временнόм интервале. При этом вычисление КПД производится по (6.1) или (6.2), где всегда учитывается разность между UСи Uост, которые легко определяются из расчета процессов в разрядном контуре, а также сравнительно просто измеряются на практике.

При резистивном заряде емкостного накопителя, величина которого C определяется требованиями разрядного контура, основной задачей является выбор зарядного резистора. Основными параметрами, определяющими его выбор, являются номинал резистора Rзар,его средняя мощность Pср, а также максимальное рабочее напряжение Umax. Номинал Rзарможет быть определен из соотношения постоянной времени цепи заряда tзар= RзарC и времени заряда, определяемого как Q = Т – t, т. е. минимальной паузы между импульсами. Для этого достаточно принять Q = (3…5)tзар, что даст значение Rзар = Q/(3…5)C. Максимальное рабочее напряжение зарядного резистора должно равняться напряжению холостого хода источника питания, так как в начале процесса заряда все напряжение источника питания прикладывается к зарядному резистору, а начальный заряд емкостного накопителя в этот момент равен нулю. Поскольку КПД зарядной цепи определен как h = Wн/Wе, то энергия, выделенная в зарядном резисторе за один цикл заряда , и отсюда

.

Тогда средняя мощность зарядного резистора

,

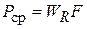где F – максимальная частота следования импульсов тока нагрузки.