 |
Главная |
Численное решение задачи Коши для обыкновенных дифференциальных уравнений
|
из
5.00
|
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
ОСНОВНЫЕ численные методы
Численное дифференцирование функций
Пусть функция f(x) дифференцируема в точке x. Тогда значение производной определяется следующими пределами [1]
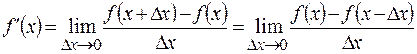
 . (1)
. (1)
Вычисление первой производной
Для вычисления производной необходимо проведение ряда операций. Можно вычислять значения функции и проводить с ними арифметические действия. Но мы не можем вычислять пределы, поскольку это требует бесконечных затрат ресурсов (времени, памяти и т.д.). Получим приближенные формулы:
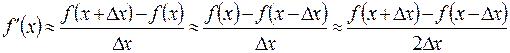 . (2)
. (2)
Пусть  - шаг разбиения. Введем обозначение
- шаг разбиения. Введем обозначение  и т.д. Тогда (2) можно переписать в виде
и т.д. Тогда (2) можно переписать в виде
 . (3)
. (3)
Первое из этих трех отношений носит название правой разностной производной, второе – левой, третье – центральной разностной производной.
Вычисление второй производной
Для приближенного вычисления второй производной в качестве примера используем формулу [1]
 , (4)
, (4)
где  определяется по формуле (3).
определяется по формуле (3).
Отметим, что значения правой и левой разностных производных в точке 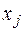 одновременно являются центральными разностными производными
одновременно являются центральными разностными производными 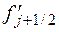 и
и  , рассчитанными соответственно в точках
, рассчитанными соответственно в точках  и
и  (см. рис. 1).
(см. рис. 1).

Рис 1. Схема численного дифференцирования
Тогда
 . (5)
. (5)
Численное интегрирование функций
Пусть необходимо вычислить определенный интеграл от некоторой непрерывной функции f(x)
 . (6)
. (6)
Численное значение интеграла равно площади, заключенной между кривой y= f(x), осью x и вертикальными прямыми x=a и x=b (рис. 2).
Разобьем отрезок интегрирования на n частей. Введем в рассмотрение последовательность узловых точек xjÎ[a,b], xj=a+jh, j=0,...,n. Величина 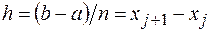 называется шагом разбиения. Обозначим fj=f(xj).
называется шагом разбиения. Обозначим fj=f(xj).
С помощью такого разбиения площадь криволинейной фигуры удается вычислить намного точнее и проще, чем без разбиения (см. рис. 2).

Рис. 2. Численное интегрирование
Таким образом, интеграл представляется суммой интегралов
 . (7)
. (7)
Метод левых прямоугольников
Вместо площади криволинейной фигуры вычисляется площадь прямоугольника, высота которого равна значению функции f(x) в крайней левой точке (рис. 3,а)
 . (8)
. (8)
 . (9)
. (9)
 а
а
|  б
б
|
Рис. 3. Методы левых (а) и правых (б) прямоугольников
Метод правых прямоугольников
Вместо площади криволинейной фигуры вычисляется площадь прямоугольника, высота которого равна значению функции f(x) в крайней правой точке (рис. 3,б)
 . (10)
. (10)
 . (11)
. (11)
Метод средних прямоугольников
Для вычисления интеграла можно использовать значение функции в середине отрезка (рис. 4,а)
 . (12)
. (12)
 . (13)
. (13)
Метод трапеций
Теперь рассмотрим численное интегрирование фигуры, полученной путем соединения отрезком прямой двух точек на графике функции. Полученная фигура является трапецией (рис. 4,б). Тогда интеграл приближенно равен ее площади
 , (14)
, (14)
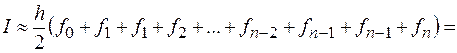
 (15)
(15)
 а
а
|  б
б
|
Рис. 4. Методы средних прямоугольников (а) и трапеций (б)
Численное решение задачи Коши для обыкновенных дифференциальных уравнений
Постановка задачи
Рассмотрим сначала следующую задачу. Пусть задано обыкновенное дифференциальное уравнение первого порядка
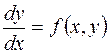 (16)
(16)
и начальное условие
 . (17)
. (17)
Такая задача называется задачей Коши для обыкновенного дифференциального уравнения.
Известно, что решение обыкновенного дифференциального уравнения первого порядка для непрерывной функции f(x) графически представляется в виде однопараметрического семейства кривых (см. например, рис. 5,а). Задание начального значения позволяет выбрать из этого семейства одну кривую, которая является решением задачи Коши.
 а а
|  б б
|
Рис. 5. Решение задачи Коши для обыкновенного дифференциального уравнения
Для численного решения задачи введем сетку xj, j=0,...,n, x0=a. Верхняя граница xn=b выбирается исходя из условий практического приложения результатов расчета. В случае равномерного разбиения с шагом h узловые точки определяются следующим образом: xj=a+jh. Обозначим yj=y(xj). Тогда
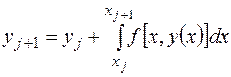 . (18)
. (18)
Однако, в отличие от задачи интегрирования функций, под знак интеграла входит неизвестная зависимость y(x). Поэтому интегрирование не может быть осуществлено точно. Но существуют способы сделать это приближенно.
Метод Эйлера
Самый простой способ заключается в использовании метода левых прямоугольников
 . (19)
. (19)
Такой метод решения задачи Коши называют методом Эйлера. Результаты применения этого метода показаны на рис. 5,б. Интегрирование на каждом шаге проводится при постоянном значении f(x,y), а значение этой функции равно производной искомой функции y(x). Отсюда следует, что метод Эйлера сводится к сдвигу вдоль касательной, проведенной к графику функции y(x) из начальной точки. Далее определяется угол наклона касательной в полученной точке и проводится новый шаг.
|
из
5.00
|
Обсуждение в статье: Численное решение задачи Коши для обыкновенных дифференциальных уравнений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

