 |
Главная |
Алгоритм определения массовых характеристик с использованием метода Монте – Карло
|
из
5.00
|
Случайным образом генерируется N – мерный вектор числовых значений z1 из заданного диапазона [z1n,z1k] с помощью встроенной функции runif()
N=5000 z1n =3.49 z1k = 3.51 z1 = runif(N,z1n,z1k)
и определятся вектор
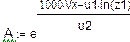
Для каждой реализации отыскивается корень уравнения
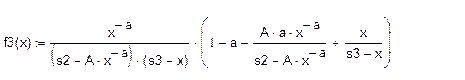
Программа вычисления чисел Циолковского по ступеням и стартовая масса приведена ниже:
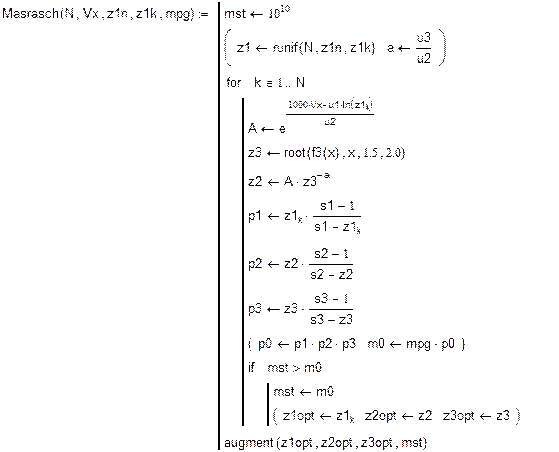
Пример
Обращение к программе с исходными данными, приведенными выше, дает следующий результат:
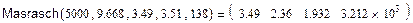
Таким образом, имеем
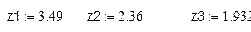
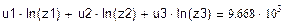
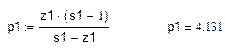
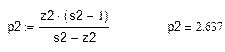
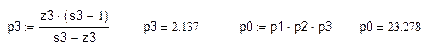

Погрешность определения стартовой массы
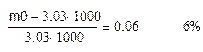
Анализ результатов показывает, что основной причиной погрешности в определении стартовой массы, является некорректное определение коэффициентов Si конструктивного совершенства блоков ракеты. Дело в том, что обычно заправка ракеты топливом рассчитывается таким образом, чтобы надежно гарантировать выведение полезного груза на орбиту. Для этого специально рассчитываются и предусматриваются дополнительные, так называемые, гарантийные запасы топлива, которые с довольно высокой степенью вероятности гарантируют выполнение задачи при сочетании самых неблагоприятных факторов (отклонение от номинальных значений конструктивных параметров ракеты, условий полета и др.). При благоприятном сочетании различных факторов это топливо (“остатки незабора”) не сгорает и вместе с конструкцией блока отделяется от ракеты. В нашем случае важно то, что это топливо не затрачивается на приращение характеристической скорости.
В рассмотренных ранее алгоритмах решение существенно зависит от назначения числа z1. Это число задавалось либо непосредственно, либо диапазоном значений. Выбор значения z1 существенно влияет на конечный результат. Чем меньше величина z1, тем меньше стартовая масса при прочих равных условиях. Однако в этом случае большая нагрузка по набору характеристической скорости будет падать на верхние ступени. Всякий раз конструктор должен анализировать возможность реализации конструкции с полученными характеристиками. Следует помнить, что это только предварительный этап анализа массовых характеристик, на котором не учитываются многие факторы, влияющие на распределение масс
Результаты решения задачи сравниваются с аналогами, если они имеются. При отсутствии аналогов можно поступить следующим образом. Например, решить задачу о распределении масс в предположении, что каждая ступень дает одинаковый вклад в приращение Vx.
Проведем расчеты для этого случая.
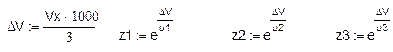
z1 = 3.375 z2 = 2.166 z3 =2.147
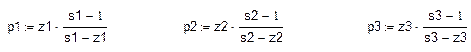
p1 = 4.11 p2 = 2.418 p3 = 2.484
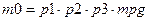
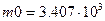
Полученное решение с точки зрения минимальной стартовой массы и распределения масс не является оптимальным, но может рассматриваться как одно из приближений, которое необходимо улучшать. Рассмотрим один из таких подходов.
|
из
5.00
|
Обсуждение в статье: Алгоритм определения массовых характеристик с использованием метода Монте – Карло |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

