Статистики Бозе-Эйнштейна и Ферми-Дирака

Одним из важнейших объектов изучения, как и классической физики, является идеальный газ, поскольку реальную систему можно считать идеальным газом в достаточно хорошем приближении. Состояние системы невзаимодействующих частиц задается с помощью N_i - чисел заполнения, характеризующих степень заполнения квантового состояния, характеризуемого данным набором i квантовых чисел, частицами системы, состоящей из множества тождественных частиц.

При рассмотрении принципа Паули, мы уже говорили о принципе неразличимости тождественных частиц. Рассмотрим случай двух тождественных частиц с точки зрения уравнения Шредингера. Из самого понятия тождественности следует, что волновая функция должна удовлетворять одному и тому же уравнению Шредингера при перемене частиц местами (при этом не изменяется также и собственное значение энергии):

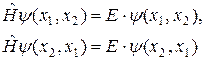(2.42)

Гамильтониан энергии представляет собой эрмитову матрицу. Напомним, что квадратную 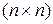- матрицу называют эрмитовой или самосопряженной, если каждый из ее элементов комплексно сопряжен элементу, симметричному данному относительно главной диагонали; иначе говоря, матрица А эрмитова, если:

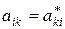
Отсюда вытекает свойство самосопряженности эрмитовой матрицы: эрмитова матрица тождественно равна своей эрмитово сопряженной, и наоборот. Например, все следующие матрицы:

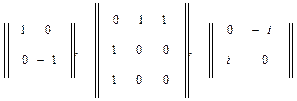
являются эрмитовыми (самосопряженными). Ввиду эрмитовости гамильтониана в случае отсутствия вырождения по энергии (при данном Е) можно заключить, что:

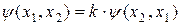(2.33)

однако

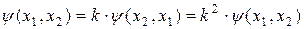
Отсюда следует, что

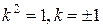(2.34)

Имеем две возможности:

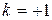, тогда 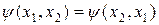- симметричная волновая функция

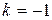, тогда 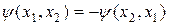- антисимметричная функция (2.35)

Когда собственное значение Е вырождено, равенство (2.33) может и не выполняться. В этом случае, однако, вместо базисных функций 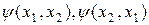можно взять их линейные комбинации:

либо 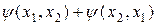- симметричная (по координатам тождественных частиц) комбинация;

либо 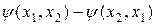- антисимметричная (по координатам тождественных частиц) комбинация.

Общими выводами из проведенных рассуждений является:

· волновую функцию системы, состоящей из двух тождественных частиц, всегда можно выбрать симметричной либо антисимметричной относительно операции перестановки этих частиц.

· если волновая функция в начальный момент времени 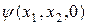является симметричной (антисимметричной), то в любой другой момент времени 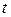эта функция 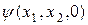сохраняет свои свойства симметрии.

Как мы уже говорили, Паули показал, что частицы, описываемые антисимметричными волновыми функциями, имею полуцелый спин, частицы, описываемые симметричными волновыми функциями – целый (или нулевой) спин. Исключения из этого правила неизвестны.

Опыт показывает, что симметрия или антисимметрия ПСИ-функции определяется спином частиц. В зависимости от характера симметрии все элементарные частицы и построенные из них системы (атомы, молекулы) делятся на два класса:

· частицы с дробным спином (электроны, протоны, нейтроны) описываются антисимметричными волновыми функциями являются фермионами.

· частицы с нулевым или целым спином описываются симметричными волновыми функциями - бозоны.

Для систем частиц, образованных бозонами, числа заполнения могут принимать любые целые значения: 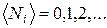Для системы частиц, образованных фермионами, числа заполнения могут принимать лишь два значения: "0" - для свободных состояний и "1" - для занятых. Это не что иное, как принцип Паули в новом выражении - 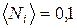. Сумма всех чисел заполнения должна быть равна числу частиц системы. Квантовая статистика позволяет подсчитать среднее число частиц в данном квантовом состоянии, т.е. определить средние числа заполнения - .

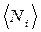Идеальный газ из бозонов (бозе-газ) описывается квантовой статистикой Бозе-Эйнштейна. Распределение бозонов по энергиям вытекает избольшого канонического распределения Гиббса (с переменным числом частиц) при условии, что число тождественных бозонов данном квантовом состоянии может быть любым:

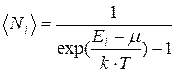
Это- распределение Бозе-Эйнштейна. 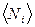-среднее число бозонов в квантовом состоянии с энергией E_i ; k - постоянная Больцмана, Т - температура, m - химический потенциал (определяет изменение внутренней энергии системы при добавлении к ней одной частицы при условии, что все остальные величины, от которых зависит внутренняя энергия, фиксированы).

Идеальный газ из фермионов (ферми – газ) описывается статистикой Ферми-Дирака:

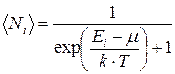
Если 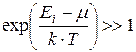, то распределение Бозе-Эйнштейна и Ферми-Дирака переходят в классическое распределение Максвелла-Больцмана :

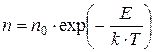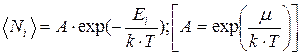
т.о., при высоких температурах оба "квантовых" газа ведут себя подобно классическому газу. Система частиц называется вырожденной, если ее свойства существенным образом отличаются от свойств систем, подчиняющихся классической статистике. Параметром вырождения называется величина А, при А<<1 происходит переход к классической статистике.

Температурой вырождения Т₀ называется температура, ниже которой отчетливо проявляются квантовые свойства.