 |
Главная |
Выражение скалярного произведения через координаты
|
из
5.00
|
Пусть даны векторы  и
и  .
.
Перемножим их скалярно, используя свойства 2) и 3):

Так как  ;
;  ,
,
то
 . (13)
. (13)
Таким образом, скалярное произведение двух векторов, заданных своими координатами, равно сумме произведений одноименных координат.
Из формул (12) и (13) можно получить следующие формулы.
1) Для вектора  его модуль вычисляется по формуле
его модуль вычисляется по формуле
 . (14)
. (14)
2) Угол между двумя векторами  ,
,  вычисляется по формуле
вычисляется по формуле  ,
,
или
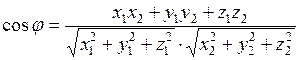 . (15)
. (15)
3) Согласно свойству 4) и формулы (13) условием ортогональности двух векторов  и
и  является равенство
является равенство
 . (16)
. (16)
4) Расстояние между точками  и
и  можно найти как длину вектора
можно найти как длину вектора  , т.е.
, т.е.
 . (17)
. (17)
Пример. Найдите скалярное произведение векторов  и
и  .
.
Решение.По формуле (13): 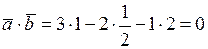 , т.е.
, т.е. 
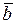 .
.
Пример.Найдите угол между векторами  и
и  .
.
Решение.По формуле (15):
 .
.
Пример. Вычислите проекцию вектора 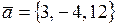 на ось, имеющую направление вектора
на ось, имеющую направление вектора  .
.
Решение.
Так как  , то сначала найдём скалярное произведение векторов
, то сначала найдём скалярное произведение векторов  и
и  :
:
 ,
,
затем длину вектора  .
.
Тогда  .
.
Здесь отрицательный знак показывает, что угол между вектором и осью проекции – тупой.
Векторное произведение векторов
Правая и левая тройки векторов
Пусть заданы три некомпланарных вектора  . Отложим их из одной точки. Будем смотреть из конца вектора
. Отложим их из одной точки. Будем смотреть из конца вектора  на векторы
на векторы 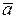 и
и 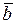 . Если кротчайший поворот от
. Если кротчайший поворот от 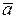 к
к 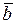 будет совершаться против часовой стрелки, то такая тройка векторов
будет совершаться против часовой стрелки, то такая тройка векторов  называется правой (рис. 6 а). Если кротчайший поворот от
называется правой (рис. 6 а). Если кротчайший поворот от 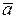 к
к 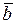 будет совершаться по часовой стрелке, то тройка векторов
будет совершаться по часовой стрелке, то тройка векторов  называется левой (рис. 6 б).
называется левой (рис. 6 б).
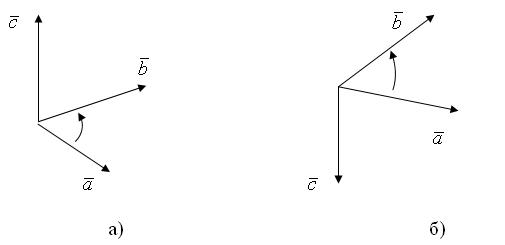
Рис. 6. Правая и левая тройки векторов
Если векторы  образуют правую тройку векторов, то система координат называется правой (рис. 7, а), в противном случае система будет левой (рис. 7, б).
образуют правую тройку векторов, то система координат называется правой (рис. 7, а), в противном случае система будет левой (рис. 7, б).

Рис.7. Правая и левая системы координат
Векторным произведением двух векторов 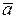 и
и 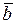 называется
называется
третий вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:
1)  , где
, где  ;
;
2) вектор  ортогонален вектору
ортогонален вектору 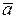 и вектору
и вектору 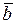 ;
;
3) векторы  образуют правую тройку векторов.
образуют правую тройку векторов.
Векторное произведение обозначается:  или [
или [ 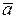 ;
; 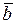 ].
].
Свойства векторного произведения
1)  .
.
2) Векторное произведение равно нулю тогда и только тогда, когда его сомножители коллинеарны (если один из векторов есть нулевой вектор, то можем считать, что 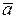 и
и 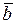 коллинеарны):
коллинеарны):

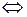
 .
.
3)  .
.
4)  .
.
5) Если векторы 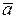 и
и 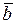 неколлинеарны, то модуль вектора
неколлинеарны, то модуль вектора  численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах 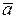 и
и 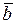 :
:
 . (18)
. (18)
Выражение векторного произведения через координаты
Пусть даны векторы  ,
,  .
.
Так как  – правая тройка векторов, то
– правая тройка векторов, то


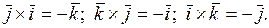
Отсюда 


Таким образом,
 (19)
(19)
Замечание.Условием коллинеарности векторов 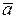 и
и 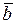 является равенство
является равенство  , т.е.
, т.е.
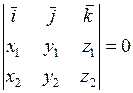 .
.
Пусть  – матрица, составленная из координат векторов
– матрица, составленная из координат векторов 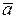 и
и 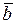 .
.
Получим из матрицы А путем поочередного вычеркивания столбцов определители  ,
,  ,
,  :
:


Тогда

Итак, условие коллинеарности двух векторов 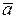 и
и 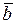 :
:

или
 .
.
Площадь треугольника
Пусть треугольник построен на векторах 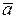 и
и 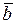 . Тогда его площадь находят по формуле
. Тогда его площадь находят по формуле
 (20)
(20)
Если векторы 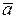 и
и 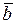 находятся в плоскости хОу, то
находятся в плоскости хОу, то  и
и

Пример.Векторы 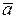 и
и 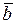 образуют угол
образуют угол  . Найдите модуль вектора
. Найдите модуль вектора 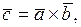 если
если  .
.
Решение. По формуле (18):
 .
.
Пример.Найдите векторное произведение векторов  и
и  .
.
Решение.По формуле (19):

Таким образом, векторным произведением векторов  и
и  является вектор
является вектор  = {-7; -7; -7}.
= {-7; -7; -7}.
Пример.Вычислите площадь параллелограмма, построенного на векторах 
Решение.1) Искомая площадь S равна модулю векторного произведения 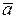 , т.е.
, т.е.  .
.
2) Вычислим векторное произведение:

Координаты векторного произведения  = { -2; -3; -7}.
= { -2; -3; -7}.
3) Тогда  (кв. ед.)
(кв. ед.)
Пример.Вычислите площадь треугольника АВС, построенного на векторах  и
и  .
.
Решение. По формуле (20): 
|
из
5.00
|
Обсуждение в статье: Выражение скалярного произведения через координаты |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

