 |
Главная |
Как производится расчет на усталость?
|
из
5.00
|
В расчетах на усталость прочность детали принято оценивать по значению расчетного коэффициента запаса n, который сравнивается со значением допускаемого коэффициента запаса прочности  , установленного соответствующими нормами. Условие прочности при таком проверочном расчете записывается в виде:
, установленного соответствующими нормами. Условие прочности при таком проверочном расчете записывается в виде:  .
.
При симметричном цикле расчетный коэффициент запаса прочности определяется как отношение предельного напряжения к расчетному.
При расчете на усталость понятие предельного напряжения относится не к материалу, а к конкретной детали.
Еще раз напомним, что предел выносливости детали при симметричном цикле существенно отличается от соответствующего предела выносливости стандартного образца, который обычно рассматривается как механическая характеристика материала.
Таким образом, расчетный коэффициент запаса при симметричном цикле определяется по формуле
 .
.
Формула для коэффициента запаса при кручении аналогична.
При асимметричном (несимметричном) цикле расчетный коэффициент запаса прочности равен:
 ,
,
где коэффициент  .
.
Важно отметить, что влияние факторов, снижающих предел выносливости, сказывается только на предельных амплитудных напряжениях цикла 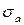 и не отражается на предельных средних напряжениях
и не отражается на предельных средних напряжениях  .
.
Коэффициент запаса n для асимметричного цикла может быть определен и непосредственно по диаграмме предельных амплитуд.
Сначала определяется коэффициент запаса не для реальной детали, а для гладкого стандартного образца  . Для этого отметим точку M (см. рис. 14.4) с координатами
. Для этого отметим точку M (см. рис. 14.4) с координатами 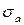 и
и  , характеризующими амплитудное и среднее напряжения заданного рабочего цикла. Соединим эту точку прямой линией с началом координат. Продолжим полученный отрезок ОМ до пересечения с кривой AСB (или
, характеризующими амплитудное и среднее напряжения заданного рабочего цикла. Соединим эту точку прямой линией с началом координат. Продолжим полученный отрезок ОМ до пересечения с кривой AСB (или 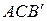 ). Полученная таким образом точка N соответствует предельному циклу. Тогда коэффициент запаса n для стандартного образца будет равен:
). Полученная таким образом точка N соответствует предельному циклу. Тогда коэффициент запаса n для стандартного образца будет равен: 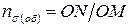 .
.
Для оценки прочности детали еще необходимо учесть, что ее предел выносливости зависит от размеров детали, состояния ее поверхности и наличия концентраторов напряжений.
В случае возникновения в опасной точке детали плоского напряженного состояния, например при совместном изгибе и кручении, общий расчетный коэффициент запаса прочности n определяется из формулы
 ,
,
где  – расчетный коэффициент запаса прочности по нормальным напряжениям
– расчетный коэффициент запаса прочности по нормальным напряжениям  , а
, а  – по касательным напряжениям
– по касательным напряжениям  .
.
ОБЩИЕ ТЕОРЕМЫ
В этой важной заключительной беседе мы рассмотрим основные теоремы механики деформируемого твердого тела, которые эффективно используются при решении ряда задач сопротивления материалов.
15.1. Как формулируется теорема Клапейрона?
Согласно этой теореме, упругая работа внешней силы при статическом приложении равна половине произведения ее окончательного значения на соответствующее этой силе перемещение.
Эту теорему в 1852 г. впервые сформулировал французский ученый Бенуа Поль Эмиль Клапейрон (Clapeyron, 1799 – 1864 гг.).
Докажем эту теорему. Определим работу, которую совершает сила 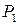 , действующая, например, на балку, изображенную на рис. 15.1, а.
, действующая, например, на балку, изображенную на рис. 15.1, а.
Будем считать, что нагрузка прикладывается к балке статически, то есть она медленно возрастает от нуля до заданной величины 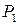 .
.
Пусть в некоторый момент сила, достигшая значения  , вызвала в месте своего приложения прогиб балки, равный
, вызвала в месте своего приложения прогиб балки, равный 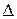 .
.
Увеличим это значение силы на бесконечно малую величину 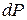 . Такое изменение нагрузки приведет к дополнительному прогибу
. Такое изменение нагрузки приведет к дополнительному прогибу  . Очевидно, что элементарная дополнительная работа определяется по формуле
. Очевидно, что элементарная дополнительная работа определяется по формуле
 .
.
 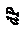  |
Тогда полная работа, совершенная внешней силой, будет равна:
 . (15.1)
. (15.1)
Для линейно деформируемой системы (график зависимости между прогибом 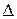 и силой P для такой системы показан на рис. 15.1, б) прогиб балки пропорционален внешней нагрузке, то есть
и силой P для такой системы показан на рис. 15.1, б) прогиб балки пропорционален внешней нагрузке, то есть
 , (15.2)
, (15.2)
где  – перемещение от силы, равной единице
– перемещение от силы, равной единице 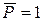 . Коэффициент
. Коэффициент  часто называют и податливостью системы.
часто называют и податливостью системы.
Дифференцируя уравнение (15.2), найдем
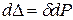 . (15.3)
. (15.3)
Подставляя (15.3) в (15.1) и учитывая, что, согласно (15.2),  , окончательно получим
, окончательно получим
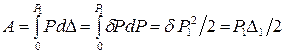 ,
,
что и требовалось доказать.
|
из
5.00
|
Обсуждение в статье: Как производится расчет на усталость? |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

