 |
Главная |
Найти: а) параметр с; б) моду; в) медиану
|
из
5.00
|
4 a). Используя свойство (5) плотности распределения, получим:  Þ
Þ  .
.
Плотность распределения имеет вид: 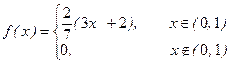
б) МодаMo СВ Х – это точка максимума функции 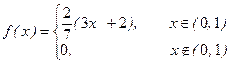 . Необходимое условие существования экстремума ‑
. Необходимое условие существования экстремума ‑ 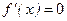 , но
, но 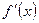 =
= 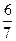 ¹0, следовательно данное распределение моды Mo не имеет.
¹0, следовательно данное распределение моды Mo не имеет.
в) Медиана Мe определяется из уравнения  . Интегрируя и подставляя пределы интегрирования, получим:
. Интегрируя и подставляя пределы интегрирования, получим: 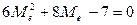 . Решая квадратное уравнение, находим корни
. Решая квадратное уравнение, находим корни 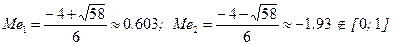 .
.
Следовательно, 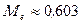 . 3
. 3
Математическое ожидание характеризует среднее значение СВ и обозначается М[X] или mx.Под символом М[X] понимают оператор математического ожидания, примененный к СВ Х. Оператор имеет различные выражения для дискретной и непрерывной СВ Х.
Математическое ожидание дискретной СВ Х есть сумма произведений всех возможных значений СВ на вероятности принятия этих значений.
М[X]=  =
= 
Математическое ожидание непрерывной СВ X есть интеграл:
М[Х] = 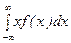
Свойства математического ожидания
1. М[С]=С
2. М[CX]=CМ[X]
3. М[X1+X2+...+Xn]= M[X1]+ M[X2]+...+ M[Xn]
4. Для независимых случайных величин X1,×X2,×...×,Xn:
М[X1×X2×...×Xn]= M[X1]× M[X2]×...× M[Xn].
ПримерИзделия испытываются на надежность. Вероятность выхода из строя за время испытания для каждого изделия равна р. Испытания заканчиваются после первого же вышедшего из строя изделия. Найти математическое ожидание СВ Х- числа проверенных изделий.
4Если X- случайное число проверенных изделий, то ряд распределения СВ Химеет вид:
| xi | ... | k | ... | |||
| pi | p | pq | pq2 | ... | рqk-1 | ... |
гдеq=1-p. Математическое ожидание Х выражается суммой ряда:
М[Х]=1p+2pq+3pq2+...+kpqk-1  +...= p(1+2q+3q2+...+kqk-1+...
+...= p(1+2q+3q2+...+kqk-1+...
Легко заметить, что ряд, стоящий в скобках представляет собой результат дифференцирования геометрической прогрессии q+q2+q3+...+qk+...= 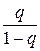 .
.
Следовательно: М[Х]=р(1+2q+3q2+...+kqk-1+...)= 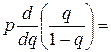
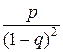 =
= 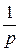 . 3
. 3
Дисперсией 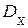 СВ Х называют математическое ожидание квадрата отклонения СВ от ее математического ожидания:
СВ Х называют математическое ожидание квадрата отклонения СВ от ее математического ожидания:
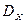 = D[X]=M[(X-M[X])2]
= D[X]=M[(X-M[X])2]
Дисперсия характеризует рассеяние значений СВ вокруг ее математического ожидания. Символ D[X] означает оператор дисперсии, примененный к СВ Х. Свойства математического ожидания позволяют получить удобную формулу для определения дисперсии:
D[X]=M[X2]-(M[X])2
Дисперсия дискретной СВ Хвычисляют по формуле:
D[X]= 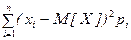
Или
D[X]= 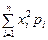 ‑ (M[X])2
‑ (M[X])2
Дисперсия непрерывной СВ Х вычисляют по формуле:
D[X]= 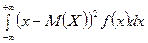
Или
D[X]= 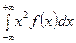 ‑(M[X]) 2
‑(M[X]) 2
Свойства дисперсии
1. D[C] = 0.
2. D[CX])=C2D[X].
3. D[X1+X2+...+Xn ]= D[X1]+D[X2] +...+D[ Xn]. (Для независимых случайных величин X1,X2,...Xn).
Средним квадратичным отклонением sх СВ Х называют квадратный корень из дисперсии:
sх = 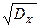 .
.
Начальным моментом k-го порядка 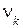 СВ Х называют математическое ожидание величины
СВ Х называют математическое ожидание величины
Хk , т.е. 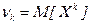
Начальный момент k-го порядка дискретной СВ выражается суммой: 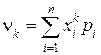 ,
,
непрерывной - интегралом:
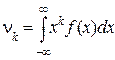
Очевидно, что при k=1  .
.
Начальные моменты высших порядков используются главным образом для вычисления центральных моментов.
Центральным моментом k-го порядка 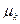 СВ Х называют математическое ожидание величины
СВ Х называют математическое ожидание величины 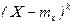 :
:
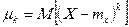
Для дискретной СВХ центральный момент выражается суммой: 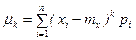 ,
,
для непрерывной - интегралом:
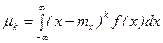 .
.
Центральный момент первого порядка  , центральный момент второго порядка – это дисперсия:
, центральный момент второго порядка – это дисперсия: 
 .
.
Центральный момент любого порядка можно выразить через начальные моменты: 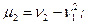
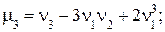
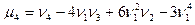 ; и т.д.
; и т.д.
Асимметрией (коэффициентом асимметрии) 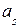 распределения СВ Х называется величина:
распределения СВ Х называется величина:
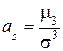 .
.
Коэффициент асимметрии характеризует “скошенность” графика плотности распределения вероятностей.
Эксцессом 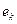 СВ Х называется величина
СВ Х называется величина
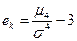 ,
,
она характеризует крутизну кривой распределения.
|
из
5.00
|
Обсуждение в статье: Найти: а) параметр с; б) моду; в) медиану |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

