Распределение Пуассона

СВ Х распределена по закону Пуассона, если онапринимает целые неотрицательные значения: 0, 1, 2, …, k, …, вероятности которых можно вычислить по формулам:

,

где k – число появлений событияАв n независимыхиспытаниях ( ), ( )‑ параметр распределения, который равен среднему числу появления события А в n испытаниях. Если вероятность появления события А в каждом испытании одинакова и равна р, то .

Распределение Пуассона является предельным для биномиального распределения, когда число испытаний n достаточно велико, а вероятность р появления события в каждом испытании мала (порядка 1/n).

Ряд распределения СВ Х , распределенной по закону Пуассона, имеет вид:

х				…	n	…
рk				…		…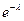

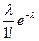
Математическое ожидание и дисперсия соответственно равны:

, D .

 

Пример.На телефонную станцию в течение часа поступают в среднем 30 вызовов. Найти вероятность того, что в течение минуты поступает не более двух вызовов.

 

4Математическое ожидание числа вызовов за минуту равно . Вероятность того, что в течение данной минуты будет получено не более двух вызовов, равна сумме вероятностей того, что в течение данной минуты будет либо 0, либо 1, либо 2 вызова. Поэтому искомая вероятность:

P(k£2) = p(X=0)+P(X=1)+P(X=2)= = + + = (1+1/2+ )»0,98. 3

Равномерное распределение

СВ Х подчинена равномерному закону распределения, если ее плотность распределения вероятностей имеет вид:

.

График плотности равномерного распределения f(x) изображен на рис.5.1.

Интегральная функция распределения F(x) равна: ,

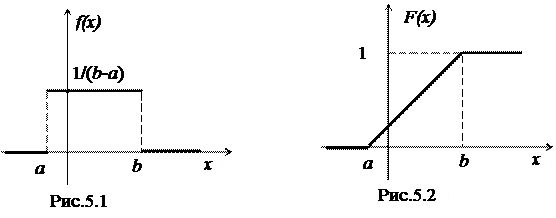ее график изображен на рис. 5.2.

Математическое ожидание, дисперсия и среднее квадратичное отклонение соответственно равны:

; D ; .

Вероятность попадания Х в заданный интервал значений определяется: .

Показательное распределение

Непрерывная СВ Х распределена по показательному (экспоненциальному) закону, если ее плотность распределения вероятностей имеет вид:

,

где l - параметр распределения.

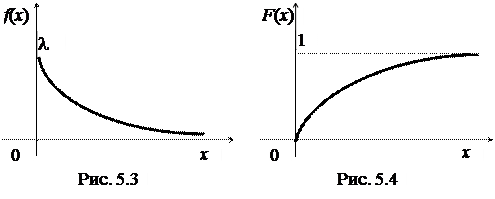
Кривая плотности распределения f(x)изображена на рис.5.3. Интегральная функция распределения равна

,

ее график показан на рис 5.4.

Математическое ожидание, дисперсия и среднее квадратичное соответственно равны:

M[X]=1/l; D[X]=1/l²; s_х=1/l;

а вероятность попадания Х в заданный интервал значений определяется следующим образом: .

 

Пример.СВ Т—время безотказной работы телевизора - имеет показательное распределение. Определить вероятность того, что время безотказной работы телевизора будет не меньше 600 часов, если среднее время работы его 400 часов.

4 По условию задачи математическое ожидание СВ Т равно 400 часов. Искомая вероятность

P(T ³ 600 )= 1- P(T<600 )= 1- F(600)=1-(1-e^-600/400 )=e^-1,5 » 0,2231. 3