Графическая работа № 5. Построение третьего вида по двум данным

Постройте третий вид по двум данным (рис. 115).

Рис. 115. Задания к графической работе № 5

§ 14. Нанесение размеров с учетом формы предмета

Основные правила нанесения размеров вам уже известны. Рассмотрим теперь на примере чертежа предмета — опоры (рис. 116) — некоторые дополнительные сведения о нанесении размеров.

Рис. 116. Нанесение размеров

Как определить, какие размеры и где необходимо нанести на чертеже предмета? Узнать это нам поможет анализ формы предмета (см. II).

Предмет, изображенный на рисунке 116. а, можно мысленно разделить на параллелепипед с кубическим отверстием и цилиндр (рис. 116, б). Их размеры и наносят на чертеже: для параллелепипеда и кубического отверстия — длину, ширину и высоту; для цилиндра— диаметр основания и высоту.

Теперь размеры каждой части указаны. Но достаточно ли их для изготовления предмета? Нет. Необходимо еще нанести размеры, определяющие взаимное положение частей предмета, т. е. координирующие размеры: 16, 18, 5 и 6 мм.

Размеры 16 и 18 мм определяют положение цилиндра относительно параллелепипеда, являющегося основанием предмета. Размеры 5 и 6 мм определяют положение куба относительно параллелепипеда.

Заметьте, что размеры, определяющие высоту цилиндра и кубического отверстия, в данном случае наносить не нужно. Высота цилиндра определяется как разность между общей высотой предмета (36 мм) и толщиной параллелепипеда (14 мм) и равна 22 мм. Высота кубического отверстия определяется высотой основания, т. е. она равна 14 мм.

Каждый размер на чертеже указывают только один раз. Например, если на главном виде (рис. 116, а) нанесен размер основания цилиндра диаметром 20, то на виде сверху его наносить не надо.

В то же время чертеж должен содержать все размеры, необходимые для изготовления предмета. Очень часто школьники забывают нанести такие размеры, как 16, 18, 5 и 6 мм, без которых невозможно определить на чертеже взаимное положение частей предмета.

На чертежах обязательно наносят габаритные размеры. Габаритными называют размеры, определяющие предельные (наибольшие и наименьшие) величины внешних (и внутренних) очертаний изделий. На рисунке 116 это размеры 67, 32, 36.

Вы знаете, что при нанесении размеров меньшие размеры располагают ближе к изображению, а большие — дальше. Так, размер 14 на главном виде (рис. 116, а) находится ближе к изображению, а 36—дальше. Благодаря соблюдению этого правила удается избежать лишних пересечений размерных и выносных линий.

Таким образом, габаритные размеры, которые всегда больше других, располагают дальше от изображения, чем остальные. Без габаритных размеров чертеж не закончен.

На рисунке I17, а и б приведены два примера нанесения размеров детали типа вал. В первом случае правильное, во втором - неудачное, с ошибками. Ошибки выделены цветом.

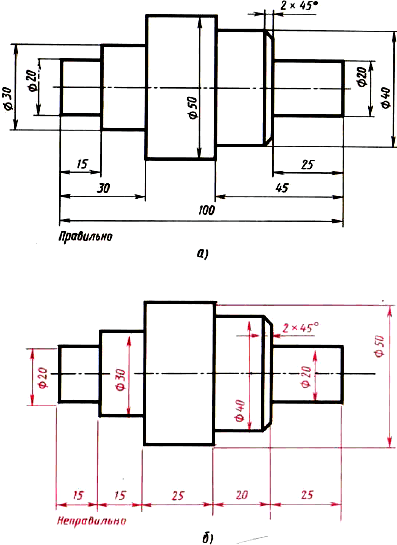
Рис. 117. Нанесение размеров

Размеры надо наносить так, чтобы удобно было читать чертеж и при изготовлении детали не выяснять что-либо путем подсчетов. На первом чертеже (рис. 117, а) длина детали —100 мм — видна сразу. На втором (рис. 117, б) —ее надо подсчитывать.

Размеры, определяющие длину цилиндров — составных частей детали, в первом случае нанесены с учетом изготовления детали. Как вы эту деталь будете изготавливать в мастерских? Сначала проточите цилиндр диаметром 40 мм на длину 45 мм, а затем диаметром 20 мм на длину 25 мм. То же с другой стороны. Во втором случае это при нанесении размеров не учтено.

Размеры наносят, как правило, вне контура изображения и так, чтобы размерные линии по возможности не пересекались между собой. Цифры пишут над размерными линиями, тогда чертеж удобно читать. На рисунке 117, б это не везде выдержано. Размеры диаметром 30, 40, 20 (справа) расположены внутри контура изображения. Размеры диаметром 20 нанесены под размерной линией. Размер диаметром 50 вынесен далеко вправо, что привело к пересечению многих выносных линий и осложнило понимание чертежа. В данном случае его удобней нанести, как на рисунке 117, а.

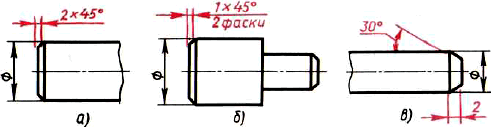
Рис. 118. Нанесение размеров фаски

Осевая (штрихпунктирная) линия должна выходить за контур изображения примерно на 3 мм и не пересекать размерное число. На рисунке 1 17, б это не выдержано. Неудачно проведены и выносные линии, они не выходят за размерные линии или проведены слишком далеко.

У деталей, имеющих форму тел вращения, часто торцовые кромки срезают на конус. Этот элемент называют фаской. Ее назначение — облегчить сборку деталей, защитить кромки от повреждения, а руки рабочего от порезов.

Наиболее часто встречаются фаски под углом 45°. Их размеры наносят записью, например 2X45°, где 2—высота фаски (рис. 118, а). Если встречается несколько одинаковых фасок, их размер наносят один раз с указанием количества (рис. 118, б).

Размеры фасок под другими углами указывают линейным и угловым размерами, а не надписью (рис. 118, в).

1. Как анализ формы предмета помогает определить размеры, необходимые для нанесения на чертеже детали?
2. Какие размеры наносят на чертеже цилиндра, конуса, прямоугольного параллелепипеда?
3. Благодаря каким знакам можно изобразить в одной проекции цилиндр и конус? призму с квадратным основанием?
4. Какие размеры на рисунке 116 определяют взаимное положение частей детали?
5. Какие размеры называют габаритными? Обязательно ли их надо наносить на чертеже?
6. Как наносят размеры фасок под углом 45°?

1. Постройте по заданию учителя наглядное изображение одной из деталей (рис. 119) и нанесите размеры.

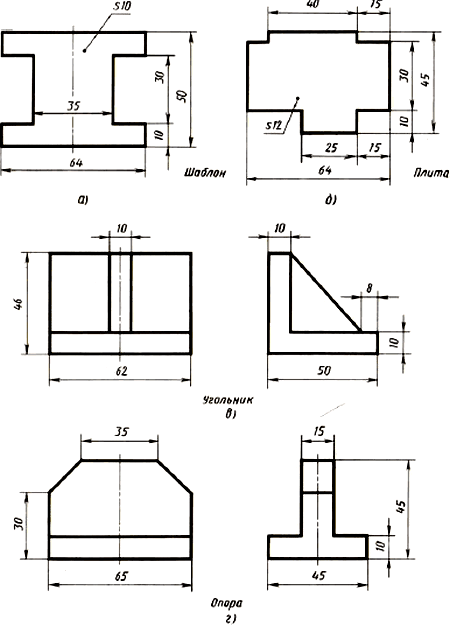
Рис. 119. Задания для упражнений

1. Постройте по аксонометрической проекции (рис. 120) три вида детали и нанесите размеры.

Рис. 120. Задания для упражнений

1. По заданию учителя перечертите один из чертежей (рис. 121), увеличив изображение в два раза. Нанесите размеры, определив их с помощью обмера изображений. На одном чертеже (рис. 121, а) сократите количество изображений.

Рис. 121. Задания для упражнений

1. Перечертите заданные изображения, увеличив их в два раза, и постройте третий вид (рис. 122). Нанесите размеры, определив их с помощью обмера изображений.

Рис. 122. Задания для упражнений

§ 15. Геометрические построения, необходимые при выполнении чертежей

При вычерчивании деталей, построении разверток поверхностей вам приходится выполнять различные геометрические построения, например делить на равные части отрезки и окружности, строить углы, выполнять сопряжения и др.

Многие из этих построений вам уже известны из уроков геометрии и других предметов, поэтому здесь они не рассматриваются. Рациональные приемы построения углов с помощью чертежных инструментов приведены на форзаце в конце книги.

15.1. Анализ графического состава изображений. Прежде чем приступить к выполнению чертежа, надо определить, какие геометрические построения потребуется применить в данном случае. Рассмотрим пример.

На рисунке 123, а приведены три проекции опоры, наглядное изображение которой дано на рисунке 74, а. Чтобы начертить этот предмет, надо выполнить ряд графических построений:

1. провести параллельные прямые;
2. построить сопряжение (скругление) двух параллельных прямых дугой заданного радиуса (рис. 123, б);
3. провести три концентрические окружности (рис. 123, в);
4. вычертить трапецию (рис. 123, г).

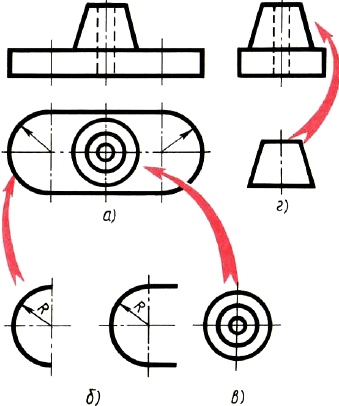
Рис. 123. Анализ графического состава изображений

Расчленение процесса выполнения чертежа на отдельные графические операции называется анализом графического состава изображений.

Определение графических операций, из которых слагается построение чертежа, облегчает его выполнение.

1. Какие геометрические построения вам известны?
2. Как называется расчленение процесса выполнения чертежа на отдельные графические операции?
3. Для чего нужен анализ графического состава изображений?

15.2. Деление окружности на равные части. Многие детали имеют равномерно расположенные по окружности элементы, например отверстия, спицы и т. д. Поэтому возникает необходимость делить окружности на равные части.

Деление окружности на четыре равные части. Чтобы разделить окружность на четыре равные части, нужно провести два взаимно перпендикулярных диаметра (см. на форзаце).

Два случая таких построений показаны на рисунке 124. На рисунке 124. а диаметры проведены по линейке и катету равнобедренного угольника, а стороны вписанного квадрата - по его гипотенузе. На рисунке 124, б, наоборот, диаметры проведены по гипотенузе угольника, а стороны квадрата — по линейке и катету угольника.

Рис. 124. Деление окружности на четыре равные части

Деление окружности на восемь равных частей. Чтобы разделить окружность на восемь равных частей, достаточно провести две пары диаметров, т. е. объединить оба случая построения квадрата (см. рис. 124). Одну пару взаимно перпендикулярных диаметров отроят по линейке и катету. другую — но гипотенузе угольника (рис. 125).

Рис. 125. Деление окружности на восемь равных частей

Деление окружности на три равные части. Поставив опорную ножку циркуля в конце диаметра (рис. 126, а), описывают дугу радиусом, равным радиусу R окружности. Получают первое и второе деление. Третье деление находится на противоположном конце диаметра.

Ту же задачу можно решить с помощью линейки и угольника с углами 30, 60 и 90°. Для этого устанавливают угольник большим катетом параллельно вертикальному диаметру. Вдоль гипотенузы из точки 1 (конца диаметра) проводят хорду, получают второе деление (рис. 126, б). Повернув угольник и проведя вторую хорду, получают третье деление (рис. 126, в).

Рис. 126. Деление окружности на три равные части: а — с помощью циркуля; б, в— с помощью угольника и линейки

Соединив точки 2 и 3 отрезком прямой, получают равносторонний треугольник.

Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности, так как сторона шестиугольника равна радиусу описанной окружности. Из противоположных концов одного из диаметров окружности (например, точек 1 и 4, рис. 127, а) описывают дуги. Точки 1, 2, 3. 4, 5, 6 делят окружность на равные части. Соединив их отрезками прямых, получают правильный шестиугольник (рис. 127, б).

Рис. 127. Деление окружности на шесть равных частей с помощью циркуля

Ту же задачу можно выполнить при помощи линейки и угольника с углами 30 и 60° (рис. 128).

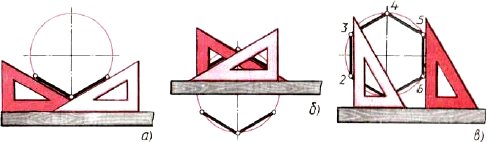
Рис. 128. Деление окружности на шесть равных частей с помощью угольника и линейки

Деление окружности на пять равных частей. Пятой части окружности соответствует центральный угол в 72° (360°:5 = 72°). Этот угол можно построить при помощи транспортира (рис. 129, а).

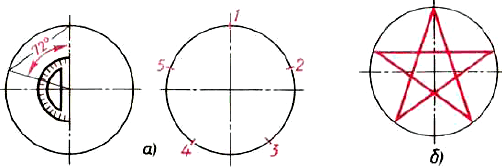
Рис. 129. Деление окружности на пять равных частей

На рисунке 129, 6 показано вычерчивание пятиконечной звезды.

Постройте с помощью линейки и угольника правильный шестиугольник, две вершины которого лежат на горизонтальной центровой линии. Выполните то же построение с помощью циркуля.

15.3. Сопряжения. У шаблона на рисунке 130 углы скруглены. Прямые линии плавно переходят в кривые. Такой же плавный переход может быть между прямыми или между двумя окружностями.

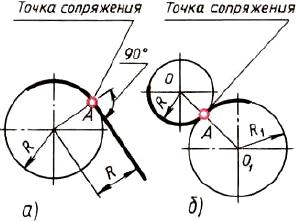
Рис. 130. Шаблон

Плавный переход одной линии в другую называют сопряжением.

Для построения сопряжений надо найти центры, из которых проводят дуги, т. е. центры сопряжений. Надо найти также точки, в которых одна линия переходит в другую, т. е. точки сопряжений.

Таким образом, для построения любого сопряжения надо найти центр сопряжения, точки сопряжений, знать радиус сопряжения.

При построении сопряжений следует иметь в виду, что переход от прямой к окружности будет плавным в том случае, если прямая касается окружности (рис. 131, а). Точка сопряжения лежит на радиусе, перпендикулярном данной прямой.

Рис. 131. Построение сопряжений

Переход от одной окружности к другой будет плавным, если окружности касаются. Точка сопряжения находится на прямой, соединяющей их центры (рис. 131. б).

Сопряжение двух прямых дугой заданного радиуса. Даны прямые, составляющие прямой, острый и тупой углы (рис. 132, а) и величина R радиуса дуги сопряжения. Требуется построить сопряжение этих прямых дугой заданного радиуса.

Рис. 132. Общий способ построения сопряжений двух пересекающихся прямых

Для всех трех случаев применяют общий способ построения.

1. Находят точку О — центр сопряжения (рис. 132, б). Он должен лежать на расстоянии R от заданных прямых. Очевидно. такому условию удовлетворяет точка пересечения двух прямых, расположенных параллельно заданным на расстоянии R от них.

Чтобы построить эти прямые, из произвольно выбранных точек каждой заданной прямой проводят перпендикуляры. Откладывают на них длину радиуса R. Через полученные точки проводят прямые, параллельные заданным.

В точке пересечения этих прямых находится центр О сопряжения.

1. Находят точки сопряжения (рис. 132, о). Для этого проводят перпендикуляры из центра сопряжения к заданным прямым. Полученные точки являются точками сопряжений.
2. Поставив опорную ножку циркуля в точку О, проводят дугу заданного радиуса R между точками сопряжений (рис. 132, в).

Сопряжение окружности и прямой дугой заданного радиуса. Даны окружность радиуса R, отрезок АВ и радиус дуги сопряжения R₁ (рис. 133).

Построение выполняют так:

1. Для нахождения центра сопряжения из точки О окружности проводят дугу вспомогательной окружности радиуса R+R₁

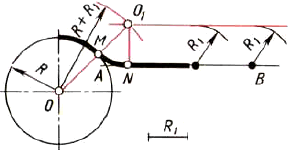
Рис. 133. Построение сопряжения дуги окружности и прямой

На расстоянии R₁ от прямой АВ , проводят параллельную ей прямую до пересечения с дугой R+R₁. Точка 0₁ будет центром сопряжения.

1. Соединив прямой точки О и 0₁, т. е. центры окружности и сопрягающей дуги, получают точку сопряжения М. Проведя из точки 0₁ перпендикуляр к прямой АВ, определяют вторую точку сопряжения N.
2. Соединив дугой R₁ точки М и N сопряжения, получают плавный переход от окружности к прямой.

15.4. Применение геометрических построений на практике. Чтобы изготовить из металлического листа деталь, например шаблон, изображенный на рисунке 130, надо прежде очертить на металле его контур, т. е. сделать разметку. Между выполнением чертежа и разметкой много общего.

При выполнении чертежа или разметки надо определить, какие геометрические построения следует при этом применить, т. е. провести анализ графического состава изображений (см. 15.1). Слева на рисунке 134 показаны эти построения.

Рис. 134. Анализ контура изображения детали

В результате анализа устанавливаем, что вычерчивание контура шаблона слагается в основном из построения угла 60° и сопряжений острого и тупого углов дугами заданных радиусов.

Какова последовательность разметки шаблона? Можно ли ее начинать с построения сопряжений? Очевидно, нет.

Правильная последовательность построения чертежа показана на рисунке 135. Сначала проводят те линии чертежа, положение которых определяется заданными размерами и не требует дополнительных построений, а затем строят сопряжения.

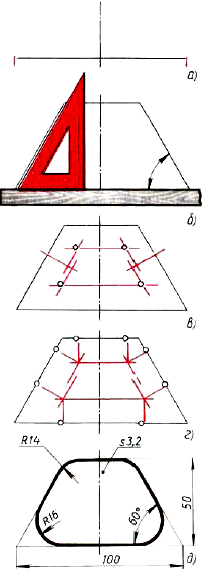
Рис. 135. Последовательность построения чертежа шаблона

Таким образом, построение ведут в такой последовательности. Вначале проводят осевую линию и прямую, на которой лежит основание шаблона (рис. 135, а). На этой прямой вправо и влево от осевой линии откладывают половину длины основания, т. е. по 50 мм. Затем строят углы 60° и проводят прямую параллельно основанию на расстоянии 50 мм от него (рис. 135, б). После этого находят центры и точки сопряжений (рис. 135, в и г). В заключение проводят дуги сопряжений. Обводят видимый контур и наносят размеры (рис. 135, д).

1. Какие углы можно построить с помощью угольников?
2. Чему равен раствор циркуля при делении окружности на шесть равных частей, на три равные части?
3. Что называется сопряжением?
4. Назовите элементы, обязательные в любом сопряжении.
5. Какие построения встретятся вам при выполнении чертежа детали, представленной на рисунке 136?

Рис. 136. Задание для упражнений

По аксонометрической проекции (рис. 137) выполните чертеж детали.

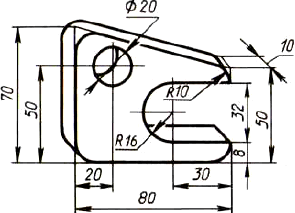
Рис. 137. Задание для упражнений

Графическая работа № 6. Чертеж детали (с использованием геометрических построений, в том числе сопряжений)

Выполните с натуры или по наглядному изображению (рис. 138) в необходимом количестве видов чертеж одной из деталей, в очертаниях которой содержатся сопряжения.

Рис. 138. Задания к графической работе № 6

§ 16. Чертежи разверток поверхностей геометрических тел

16.1. Чертежи разверток поверхностей призм и цилиндров.

Для изготовления ограждений станков, вентиляционных труб и некоторых других изделий вырезают из листового материала их развертки.

Развертка поверхностей любой прямой призмы представляет собой плоскую фигуру, составленную из боковых граней — прямоугольников и двух оснований — многоугольников.

Например, у развертки поверхностей шестиугольной призмы (рис. 139, б) все грани — равные между собой прямоугольники шириной а и высотой h, а основания — правильные шестиугольники со стороной, равной а.

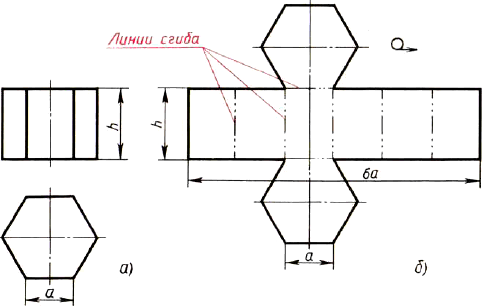
Рис. 139. Построение чертежа развертки поверхностей призмы: а — два вида; б — развертка поверхностей

Таким образом, можно построить чертеж развертки поверхностей любой призмы.

Развертка поверхностей цилиндра состоит из прямоугольника и двух кругов (рис. 140, б). Одна сторона прямоугольника равна высоте цилиндра, другая — длине окружности основания. На чертеже развертки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру оснований цилиндра.

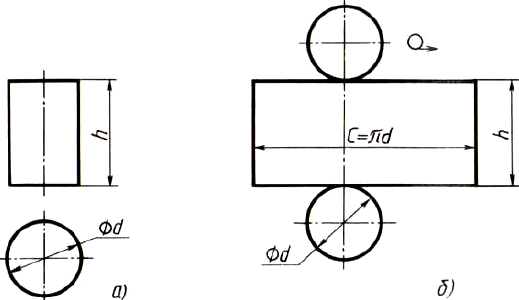
Рис. 140. Построение чертежа развертки поверхностей цилиндра: а - два вида; б - развертка поверхностей

16.2. Чертежи разверток поверхностей конуса и пирамиды.

Развертка поверхностей конуса представляет собой плоскую фигуру, состоящую из сектора - развертки боковой поверхности и круга - основания конуса (рис. 141, 6).

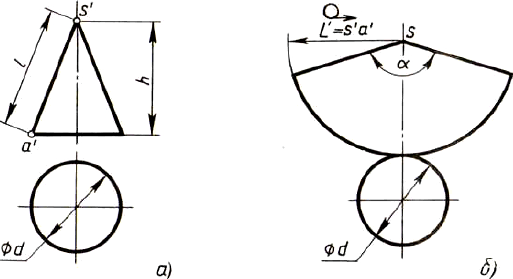
Рис. 141. Построение чертежа развертки поверхностей конуса: а — два вида; б — развертка поверхностей

Построения выполняются так:

1. Проводят осевую линию и из точки s' на ней описывают радиусом, равным длине s'a' образующей конуса, дугу окружности. На ней откладывают длину окружности основания конуса.

Точку s' соединяют с концевыми точками дуги.

1. К полученной фигуре — сектору пристраивают круг. Диаметр этого круга равен диаметру основания конуса.

Длину окружности при построении сектора можно определить по формуле C = 3.14xD.

Угол а подсчитывают по формуле а = 360°хD/2L, где D — диаметр окружности основания, L —длина образующей конуса, ее можно подсчитать по теореме Пифагора.

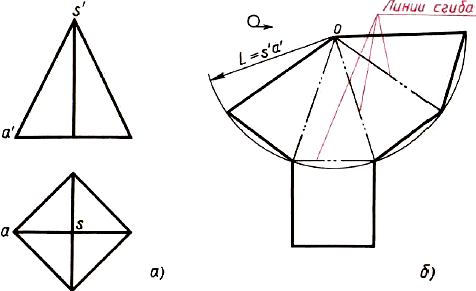
Рис. 142. Построение чертежа развертки поверхностей пирамиды: а — два вида; б — развертка поверхностей

Чертеж развертки поверхностей пирамиды строят так (рис. 142, б):
Из произвольной точки О описывают дугу радиуса L, равного длине бокового ребра пирамиды. На этой дуге откладывают четыре отрезка, равные стороне основания. Крайние точки соединяют прямыми с точкой О. Затем пристраивают квадрат, равный основанию пирамиды.

Обратите внимание, как оформляют чертежи разверток. Над изображением выносят специальный знак. От линий сгиба, которые проводят штрихпунктирнои с двумя точками, проводят линии-выноски и пишут на полке «Линии сгиба».

1. Как построить чертеж развертки поверхностей цилиндра?
2. Какие надписи наносят на чертежах разверток поверхностей предметов?

§ 17. Порядок чтения чертежей деталей

Чтение чертежа заключается в представлении по плоским изображениям объемной формы предмета и в определении его размеров. Эту работу рекомендуется проводить в такой последовательности:

1. Прочитать основную надпись чертежа. Из нее можно узнать название детали, наименование материала, из которого ее изготовляют, масштаб изображений и другие сведения.
2. Определить, какие виды детали даны на чертеже, какой из них является главным.
3. Рассмотреть виды во взаимной связи и попытаться определить форму детали со всеми подробностями. Этой задаче помогает анализ изображений, данных на чертеже. Представив по чертежу геометрическую форму каждой части детали, мысленно объединяют их в единое целое.
4. Определить по чертежу размеры детали и ее элементов. Приведем пример чтения чертежа детали (вначале даны вопросы к чертежу, а затем ответы на них).

Вопросы к чертежу (рис. 143. Вопросы составлены в последовательности, соответствующей правильному порядку чтения чертежей)

1. Как называется деталь?
2. Из какого материала ее изготовляют?
3. В каком масштабе выполнен чертеж?
4. Какие виды содержит чертеж?
5. Сочетанием каких геометрических тел определяется форма детали?
6. Опишите общую форму детали.
7. Чему равны габаритные размеры деталей и размеры отдельных частей?

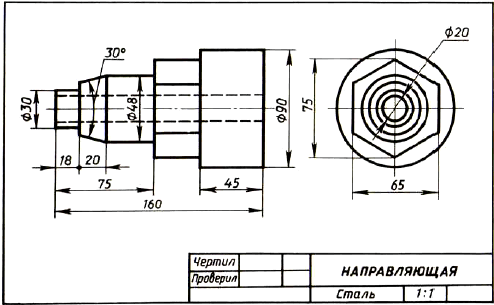
Рис. 143. Чертеж детали

Ответы на вопросы к чертежу (см. рис. 143).

1. Деталь называется «направляющая».
2. Изготовляют деталь из стали.
3. Масштаб чертежа 1:1, т. е. деталь изображена в натуральную величину.
4. Чертеж содержит два вида: главный и слева.
5. Выделив части детали, рассмотрим их слева направо, сопоставляя оба вида.

Крайняя левая часть на главном виде имеет форму прямоугольника, а на виде слева — окружности. Значит, это цилиндр. так как такие проекции характерны для цилиндра.

Вторая слева часть на главном виде имеет форму трапеции. На виде слева она показана двумя окружностями. Такие проекции может иметь только усеченный конус.

Третья часть, как и первая, показана на главном виде прямоугольником, а на виде слева — окружностью. Значит, она имеет также форму цилиндра.

Четвертая часть на главном виде имеет очертание прямоугольника, внутри которой проведены две горизонтальные линии, а на виде слева — шестиугольника. Такие изображения характерны для шестиугольной призмы.

Крайняя справа часть показана прямоугольником на главном виде и окружностью на виде слева. Мы знаем, что такие изображения определяют цилиндр.

По штриховым линиям на главном виде и по окружности самого меньшего диаметра на виде слева можно сделать вывод, что внутри детали имеется сквозное цилиндрическое отверстие.

1. Объединив все части, устанавливаем общую форму предмета (рис. 144). Она представляет собой сочетание цилиндров, усеченного конуса и шестиугольной призмы, расположенных на одной оси. Вдоль оси детали проходит сквозное цилиндрическое отверстие.

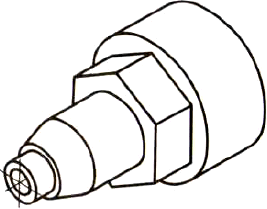
Рис. 144. Изометрическая проекция детали

1. Габаритные (наибольшие и наименьшие) размеры детали таковы: длина 160 мм, диаметр 90 мм, диаметр отверстия 20 мм. Диаметр крайней левой цилиндрической части 30 мм, длина 18 мм. Высота усеченного конуса 20 мм, угол при вершине 30°, диаметр большего основания 48 мм.

Такой же диаметр имеет следующая цилиндрическая часть. Длина цилиндра определяется как разность между размерами 75 и 38, т. е. равна 37 мм.

Два размера части детали, имеющей форму шестиугольной призмы, нанесены на виде слева: между параллельными гранями —65 мм, между двумя ребрами —75 мм. Длина этой части не указана, она определяется вычитанием из габаритного размера (160) размеров 75 и 45. Диаметр наибольшего цилиндра 90 мм, длина его 45 мм. Диаметр отверстия 20 мм.

Прочитайте чертеж на рисунке 145.

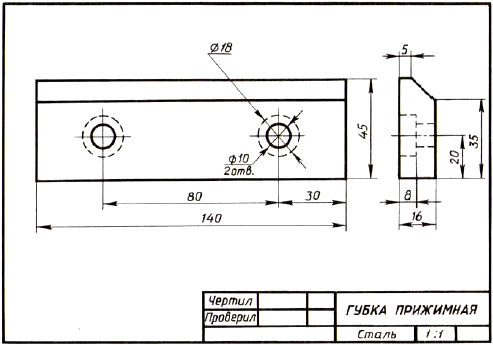
Рис. 145. Задание для упражнений

Вопросы к чертежу

1. Как называется деталь?
2. Из какого материала она изготовляется?
3. Какие виды даны на чертеже?
4. Сочетанием каких геометрических тел определяется форма детали?
5. Какие элементы детали показаны на главном виде двумя окружностями диаметром 10?
6. Изображением каких элементов являются окружности диаметром 18 и почему они проведены на главном виде штриховыми линиями?
7. Каковы габаритные размеры детали?