Анализ геометрической формы предмета

На рисунке 72 вы видите изображения некоторых геометрических тел. Форма каждого из них имеет свои характерные признаки. По этим признакам мы отличаем цилиндр от конуса, а конус от пирамиды. С большинством этих тел вы знакомы. Мы говорим «куб», и каждый представляет себе его форму. Говорим «шар», и опять в нашем сознании возникает образ определенного геометрического тела.

Присмотритесь к окружающим нас предметам. Они имеют форму геометрических тел или представляют собой их сочетания.

Рис. 72. Геометрические тела

В основе формы деталей машин и механизмов также находятся геометрические тела. Взгляните на рисунок 73. Здесь изображены различные детали. Часть из них самой простой формы. Скажите, какую форму имеют ось и ролик. А какова форма прокладки?

Рис. 73. Различные детали имеют в своей основе геометрические тела

О таких деталях, как ось и ролик, мы скажем, что они цилиндрические, а о прокладке — что она призматическая.

Другие детали имеют более сложную форму. Они представляют собой совокупность геометрических тел. Например, валик (рис. 73) образуется в результате добавления к цилиндру другого цилиндра меньших размеров. А втулка представляет собой цилиндр, из которого удален другой цилиндр меньшего диаметра.

Труднее понять по чертежу форму более сложной детали, например вилки.

Как легче определить форму предмета по чертежу? Для этого сложную по форме деталь мысленно расчленяют на отдельные составляющие ее части, имеющие форму различных геометрических тел. Рассмотрим пример.

На рисунке 74, а дано изображение опоры. Какова ее форма? Она слагается из прямоугольного параллелепипеда, двух полуцилиндров и усеченного конуса. В детали имеется цилиндрическое отверстие (рис. 74. б). После такого «расчленения» форму детали определить легче.

Рис. 74. Анализ геометрической формы опоры

Мысленное расчленение предмета на составляющие его геометрические тела называют анализом геометрической формы.

1. Какие геометрические тела вам известны?
2. Назовите предметы, имеющие форму шара, цилиндра, конуса, призмы.
3. Как называется процесс мысленного расчленения предмета на геометрические тела, образующие его поверхность?
4. Для чего нужен анализ геометрической формы предмета?

Определите, поверхности каких геометрических тел образуют форму предметов, изображенных на рисунке 75.

Рис. 75. Задание для упражнений

§ 11. Чертежи и аксонометрические проекции геометрических тел

Итак, вы уже знаете, что форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как изображаются геометрические тела.

11.1. Проецирование куба и прямоугольного параллелепипеда. Куб располагают так, чтобы его грани были параллельны плоскостям проекций. Тогда они изобразятся на параллельных им плоскостях проекций в натуральную величину — квадратами, а на перпендикулярных плоскостях отрезками прямых (рис. 76).

Рис. 76. Куб и параллелепипед: а — проецирование: б, г — чертежи в системе прямоугольных проекций: в, д — изометрические проекции

Проекциями куба являются три равных квадрата.

На чертеже куба и параллелепипеда указывают три размера: длину, высоту и ширину.

На рисунке 77 деталь образована двумя прямоугольными параллелепипедами, имеющими по две квадратные грани. Обратите внимание, как нанесены на чертеже размеры. Плоские поверхности отмечены тонкими пересекающимися линиями.

Рис. 77. Изображение детали в одном виде

Благодаря условному знаку форма детали ясна и по одному виду.

11.2. Проецирование правильных треугольной и шестиугольной призм. Основания призм, параллельные горизонтальной плоскости проекций, изображаются на ней в натуральную величину, а на фронтальной и профильной плоскостях -- отрезками прямых. Боковые грани изображаются без искажения на тех плоскостях проекций, которым они параллельны, и в виде отрезков прямых на тех, которым они перпендикулярны (рис. 78). Грани. наклоненные к плоскостям проекций, изображаются на них искаженными.

Рис 78. Призмы: а. г — проецирование; б, д — чертежи в системе прямоугольных проекции: в, с - изометрические проекции

Размеры призм определяются их высотой и размерами фигуры основания. Штрихпунктирнымн линиями на чертеже проведены оси симметрии.

Строить изометрические проекции призмы начинают с основания. Затем из каждой вершины основания проводят перпендикуляры, на которых откладывают отрезки, равные высоте, и через полученные точки проводят прямые, параллельные ребрам основания.

Чертеж в системе прямоугольных проекций также начинают выполнять с горизонтальной проекции.

11.3. Проецирование правильной четырехугольной пирамиды. Квадратное основание пирамиды проецируется на горизонтальную плоскость Н в натуральную величину. На нем диагоналями изображаются боковые ребра, идущие от вершин основания к вершине пирамиды (рис. 79).

Рис. 79. Пирамида: проецирование: б чертеж в системе прямоугольных проекций; в изометрический проекции

Фронтальная и профильная проекции пирамиды — равнобедренные треугольники.

Размеры пирамиды определяются длиной b двух сторон ее основания и высотой h.

Изометрическую проекцию пирамиды начинают строить с основания. Из центра полученной фигуры проводят перпендикуляр, откладывают на нем высоту пирамиды и соединяют полученную точку с вершинами основания.

11.4. Проецирование цилиндра и конуса. Если круги, лежащие и основаниях цилиндра и конуса, расположены параллельно горизонтальной плоскости H, их проекции на эту плоскость будут также кругами (рис. 80, б и д).

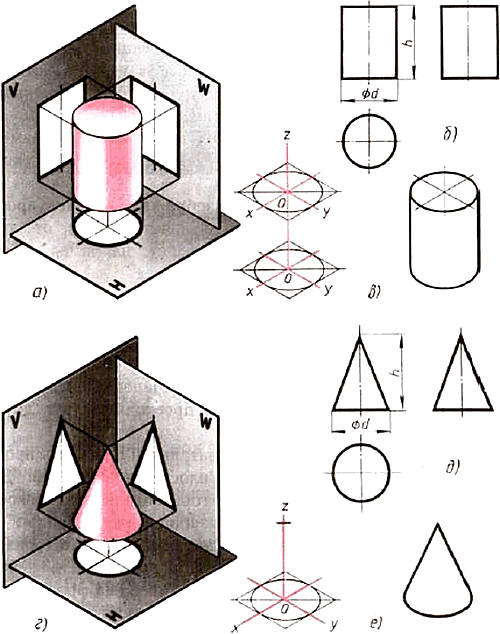
Рис. 80. Цилиндр и конус: а, г — проецирование; б, д чертежи в системе прямоугольных проекций; в. е — изометрические проекции

Фронтальная и профильная проекции цилиндра в этом случае прямоугольники, а конуса — равнобедренные треугольники.

Заметьте, что на всех проекциях следует наносить оси симметрии, с проведения которых и начинают выполнение чертежей цилиндра и конуса.

Фронтальная и профильная проекции цилиндра одинаковы. То же можно сказать о проекциях конуса. Поэтому в данном случае профильные проекции на чертеже лишние. Кроме того, благодаря значку "диаметр" можно представить форму цилиндра по одной проекции (рис. 81). Отсюда следует, что в подобных случаях нет необходимости в трех проекциях.

Рис. 81. Изображение цилиндра в одном виде

Размеры цилиндра и конуса определяются их высотой h и диаметром основания d. Способы построения изометрической проекции цилиндра и конуса одинаковы. Для этого проводят оси х и у, на которых строят ромб. Стороны его равны диаметру основания цилиндра или конуса. В ромб вписывают овал (см. рис. 66).

11.5. Проекции шара. Все проекции шара — круги, диаметр которых равен диаметру шара (рис. 82). На каждой проекции проводят центровые линии.

Рис. 82. Проекции шара

Благодаря знаку "диаметр" шар можно изображать в одной проекции. Но если по чертежу трудно отличить сферу от других поверхностей, добавляют слово «сфера», например: «Сфера диаметром 45».

11.6. Проекции группы геометрических тел. На рисунке 83 даны проекции группы геометрических тел. Можете ли вы сказать, сколько геометрических тел входит в эту группу? Какие это тела?

Рис. 83. Чертеж группы геометрических тел

Рассмотрев изображения, можно установить, что на нем даны конус, цилиндр и прямоугольный параллелепипед. Они различно расположены относительно плоскостей проекций и друг друга. Как именно?

Ось конуса перпендикулярна горизонтальной плоскости проекций, а ось цилиндра — профильной плоскости проекций. Две грани параллелепипеда параллельны горизонтальной плоскости проекций. На профильной проекции изображение цилиндра находится справа от изображения параллелепипеда, а на горизонтальной — ниже. Это значит, что цилиндр расположен впереди параллелепипеда, поэтому часть параллелепипеда на фронтальной проекции показана штриховой линией. По горизонтальной и профильной проекциям можно установить, что цилиндр касается параллелепипеда.

Фронтальная проекция конуса касается проекции параллелепипеда. Однако, судя по горизонтальной проекции, параллелепипед не касается конуса. Конус расположен левее цилиндра и параллелепипеда. На профильной проекции он частично их закрывает. Поэтому невидимые участки цилиндра и параллелепипеда показаны штриховыми линиями.

Как изменится профильная проекция на рисунке 83, если из группы геометрических тел удалить конус?

Занимательные задачи

1. На столе лежат шашки, как показано на рисунке 84, а. Сосчитайте по чертежу, сколько шашек находится в первых ближних к вам столбиках. Сколько всего шашек лежит на столе? Если вы затрудняетесь сосчитать их по чертежу, попробуйте сначала сложить шашки в столбики, пользуясь чертежом. Теперь попробуйте правильно ответить на вопросы.

Рис. 84. Задания для упражнений

1. На столе в четыре столбика расположены шашки. На чертеже они показаны двумя проекциями (рис. 84, б). Сколько шашек на столе, если черных и белых поровну? Для решения этой задачи нужно не только знать правила проецирования, но и уметь логически рассуждать.

§ 12. Проекции вершин, ребер и граней предмета

12.1. Как изображают элементы предметов. Любая точка или отрезок на изображении предмета является проекцией того или иного элемента: вершины, ребра, грани, кривой поверхности и т. п. (рис. 85). Поэтому изображение любого предмета сводится к изображению его вершины, ребер, граней и кривых поверхностей.

Рис. 85. Элементы поверхности предмета

Рассмотрим этот процесс на примере построения прямоугольных проекций предмета (рис. 86).

Расположим предмет в пространстве так, чтобы каждая из двух параллельных между собой граней была параллельна одной из плоскостей проекций. Тогда эти грани изобразятся на соответствующих плоскостях проекций без искажения.

Проведем через вершины предмета проецирующие лучи, перпендикулярные плоскостям проекций, и отметим точки пересечения их с плоскостями V, H и W.

Предмет так расположен относительно плоскостей проекций, что на одном проецирующем луче оказалось по две вершины, поэтому их проекции слились в одну точку. Так, вершины А и В лежат на одном луче, перпендикулярном горизонтальной плоскости проекций H. Их горизонтальные проекции а и b совпали. Вершины А и С лежат на одном луче, проецирующем эти точки на фронтальную плоскость проекций. Их фронтальные проекции а' и с' также совпали. На профильной плоскости проекций W в одну точку (b" и d") спроецпронались вершины В и D.

Из двух совпадающих на изображении точек одна является изображением видимой вершины, другая — закрытой (невидимой). На горизонтальмой проекции будет видима та вершина, которая расположена в пространстве выше. Так, вершина А видима, вершина В невидима. На фронтальной проекции видимой будет та вершина, которая находится ближе к нам. Отсюда а' изображение видимой вершины А, с' — изображение невидимой вершины С, она закрывается при проецировании вершиной А. На изображении обозначение проекций невидимых точек берут иногда в скобки.

Соединив попарно точки на фронтальной, горизонтальной и профильной проекциях, получим изображения ребер предмета. Например, ас — горизонтальная проекция ребра АС, а'b' фронтальная проекция ребра АB

Рис. 86. Изображения предмета

На рисунке 86 видно, что если ребро параллельно плоскости проекций, то оно на этой плоскости изображается без искажения, или, как говорят, в истинную (натуральную) величину. В этом случае проекция ребра и само ребро равны между собой. Например, проекция а'b' — истинная величина ребра АВ на фронтальной, а проекция а"b"— на профильной плоскости проекций.

Если ребро перпендикулярно плоскости проекций, оно проецируется на нее в точку. Так, на фронтальную плоскость проекций в точку спроецировалось ребро АС, на горизонтальную плоскость—ребро АВ, на профильную — ребро BD и т. д.

Построив проекции ребер, видим, что на изображении они ограничивают проекции граней. Как и ребро, грань, параллельная плоскости проекций, проецируется на нее без искажения. Например, на профильную плоскость проекций без искажения спроецировалась грань, в которой лежат точки А, В и С. На горизонтальную плоскость проекций спроецировались без искажения нижняя и верхняя грани и т. д. Найдите эти грани на чертеже предмета в системе прямоугольных проекций.

Если грань перпендикулярна плоскости проекций, она проецируется на нее в отрезок прямой.

Таким образом, каждый отрезок прямой на изображении — это проекция ребра или проекция плоскости, перпендикулярной плоскости проекций. Ребра и грани предмета, наклоненные к плоскости проекций, проецируются на нее с искажением. Найдите такие ребра и грань на рисунке 86.

Строя чертеж, надо четко представлять, как изобразится на нем каждая вершина, ребро и грань предмета. Читая чертеж, надо представить, изображение какой части предмета скрыто за каждой точкой, отрезком или фигурой.

Следует помнить, что каждый вид— это изображение всего предмета, а не одной его стороны. Разница заключается лишь в том, что одни грани спроецируются в истинную фигуру, другие— в отрезки прямых.

1. В каком случае на изображении проекции точек совпадают? Какая из двух точек, проекции которых на горизонтальной плоскости совпали, будет видимой?

2. В каком случае отрезок прямой (ребро) проецируется в истинную величину? в точку?

3. В каком случае грань (часть плоскости) проецируется в отрезок прямой? В каком случае она спроецируется в истинную величину?

Рис. 87. Задания для упражнений

1. На рисунке 87, а даны наглядное изображение и три проекции детали. На чертеже показаны проекции точки А, являющейся одной из вершин детали.

1. Как называются заданные проекции детали?
2. Перечертите в рабочую тетрадь или перенесите на кальку проекции детали. Нанесите на них проекции точек В и С.
3. Выделите одним цветом на проекциях ребро ВС. Укажите, на какие плоскости проекций это ребро спроецировалось в истинную величину.
4. Выделите (раскрасьте) одним цветом на всех проекциях ту грань детали, которая не параллельна ни одной из плоскостей проекций.

2. На рисунке 87, б дано изображение детали.

1. Сосчитайте, сколько вершин имеет изображенный предмет. Если вы затрудняетесь сделать подсчет, обозначьте вершины буквами.
2. Сосчитайте, сколько ребер и граней у предмета.
3. Сколько у предмета ребер и граней, параллельных горизонтальной плоскости проекций? Покажите их на проекциях.
4. Сколько ребер и граней, перпендикулярных горизонтальной плоскости проекций? Покажите их на изображении. Если вы затрудняетесь решить задачу, сделайте предмет из какого-либо материала и поставьте его, как на рисунке 87. Пусть плоскость стола — это горизонтальная плоскость проекций. Попробуйте теперь, сравнивая изображение и предмет, правильно ответить на вопросы.

Рис. 88. Изображение элементов поверхности детали

3. На рисунке 88 грани предмета выделены цветом. Обозначьте вершины буквами или цифрами. Проанализируйте, как расположены грани предмета относительно плоскостей проекций. Ответ запишите в рабочей тетради.

4. Перечертите или перенесите на кальку рисунок 89 и выделите на всех проекциях соответствующие грани тем же цветом, что и на наглядных изображениях.

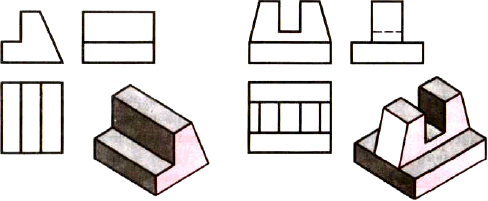
Рис. 89. Задания для упражнений

5. На рисунке 90 даны изображения трех предметов. Проекции их граней обозначены буквами. Напишите, как расположены в каждом случае относительно фронтальной плоскости проекций эти грани. Пример записи: А — параллельно, Б — перпендикулярно, В — наклонно.

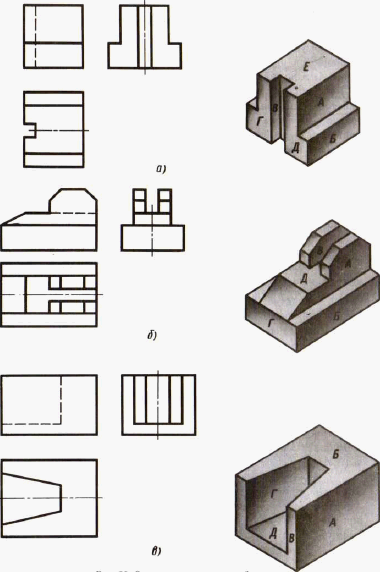
Рис. 90. Задания для упражнений

12.2. Построение проекций точек на поверхности предмета. Теперь рассмотрим способы построения проекций точек, лежащих на поверхностях предметов.

На рисунке 91 изображена шестиугольная пирамида. На линии, являющейся проекцией ребра, задана фронтальная проекция а точки А. Как найти ее остальные проекции?

Рис. 91. Построение проекций точки, лежащей на ребре пирамиды

Рассуждают так. Точка находится на ребре предмета. Проекции точки должны лежать на проекциях этого ребра. Следовательно, нужно сначала найти проекции ребра, а затем при помощи линий связи отыскать проекции точки.

Чтобы построить профильную проекцию предмета и, в частности, профильную проекцию ребра, на котором находится точка А, удобно воспользоваться постоянной прямой. Так называют линию, которую проводят справа от вида сверху под углом 45° к рамке чертежа (рис. 91). Линии связи, идущие от вида сверху, доводят до постоянной прямой. Из точек их пересечения проводят перпендикуляры к горизонтальной прямой и строят профильную проекцию.

Рис. 92. Построение постоянной прямой

Расположение постоянной прямой определяет место строящегося вида (рис. 91). Но если три вида уже построены, как на рисунке 92, а, нужно найти точку, через которую пройдет постоянная прямая. Для этого достаточно продолжить до взаимного пересечения горизонтальную и профильную проекции оси симметрии. Через полученную точку k (рис. 92, б) проводят прямую под углом 45° к осям. Это и будет постоянная прямая.

Если осей симметрии на чертеже нет, то продолжают до пересечения в точке k₁горизонтальную и профильную проекции граней, проецирующихся в виде отрезков прямых. Через точку k₁ проводят постоянную прямую.

А теперь вернемся к рисунку 91. Проекции ребра, на котором лежит точка А, выделены голубым цветом. Горизонтальная проекция точки А должна лежать на горизонтальной проекции ребра. поэтому проводим из точки а' вертикальную линию связи. В месте ее пересечения с проекцией ребра находится точка а — горизонтальная проекция точки А.

Профильная проекция а" точки А лежит на профильной проекции ребра. Ее можно определить и как точку пересечения линий связи.

Мы рассмотрели, как находят на чертеже проекции точек, лежащих на ребрах предметов. Однако часто приходится строить проекции точек, лежащих не на ребрах, а на гранях. Например, чтобы просверлить в детали отверстие, надо определить, где находится его центр.

Чтобы по одной проекции точки, лежащей на грани предмета, найти остальные, нужно прежде всего найти проекции этой грани. Такие упражнения вы уже выполняли (см. рис. 89). Затем при помощи линий связи надо отыскать проекции точки, которые должны лежать на проекциях грани.

Линию связи сначала проводят к той проекции, на которой грань изображается в виде отрезка прямой.

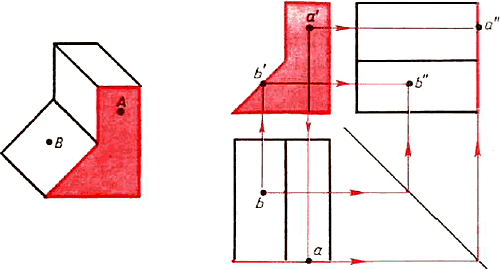
Рис. 93. Построение проекций точки, лежащей на поверхности предмета

На рисунке 93 проекции грани, содержащие проекции точки А, выделены цветом. Точка A задана фронтальной проекцией а'. Горизонтальная проекция а этой точки должна лежать на горизонтальной проекции грани. Для ее нахождения проводят вертикальную линию связи из точки а'.

Чтобы найти профильную проекцию, нужно из точки а' провести горизонтальную линию связи. В месте ее пересечения с отрезком прямой — проекцией грани лежит точка а".

Построение проекций точки В, изданной горизонтальной проекцией b, также показано линиями связи со стрелками.

1. На рисунке 94, а, б даны чертежи в системе прямоугольных проекций и наглядные изображения предметов. На видах буквами обозначены проекции вершин. Перечертите или перенесите на кальку заданные изображения. Обозначьте буквами остальные проекции вершин. Найдите эти вершины на наглядных изображениях и обозначьте их буквами.

Рис. 94. Задания для упражнений

2. Перечертите или перенесите на кальку заданные изображения (рис. 95) и постройте недостающие проекции точек, заданных на ребрах предмета. Выделите цветом проекции ребер (для каждого ребра свой цвет), содержащих точки. Нанесите точки на аксонометрической проекции и выделите теми же цветами ребра, на которых лежат точки.

Рис. 95. Задание для упражнений

3. Перечертите или перенесите на кальку рисунок 96. Постройте недостающие проекции точек, заданных на видимых поверхностях предмета. Выделите цветом проекции поверхностей, на которых лежат точки (для каждой поверхности свой цвет). Выделите поверхности предмета на наглядном изображении теми же цветами, что и на чертеже, и нанесите точки.

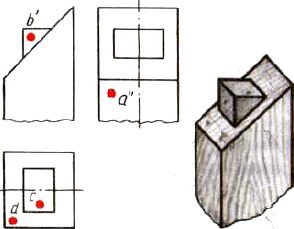
Рис. 96. Задание для упражнений

4. Перечертите или перенесите на кальку рисунок 97. Постройте недостающие проекции точек и обозначьте их буквами. Выделите цветом, как и в предыдущем задании, проекции поверхностей, на которых лежат эти точки.

Рис. 97. Задание для упражнений