ТЕМА 2. ЛИНЕЙНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ

2015-11-20

950

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒

В статистическом анализе различают два типа регрессионных моделей: простую и множественную.

I. Парная (простая) регрессия

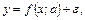(2.1)

где y – эндогенная, x – экзогенная и – случайная «шоковая» переменная, a – неизвестный вектор параметров модели.

Под термином «шоковая» переменная в регрессии понимают не только случайные (переменные погрешности) модели, но и экзогенные (факторные) переменные, которые считаются несущественными (незначимыми) по степени влияния на эндогенную переменную. В инженерной литературе эта переменная называется шумом, чтобы отличить ее от понятия полезного сигнала модели, который формируют существенные экзогенные переменные.

По степени владения априорной информацией возникают различные задачи эконометрического анализа:

при неизвестной функции взаимосвязи возникает задача подбора структуры (формы) модели, частными случаями которой являются модели с заданной функцией ( с точностью до неизвестных параметров a);

при заданной форме (функции ) возникают задачи оценивания неизвестных параметров a, которые существенно облегчаются, если функция – линейная по параметрам a. Следует заметить, что нелинейность функции по экзогенным переменным не осложняет процесс (выбор методов) оценивания параметров. Например, модель:

относится к классу линейных моделей по параметрам 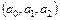и нелинейных относительно экзогенной переменной х;

при недоступности точного измерения экзогенной переменной возникает задача оценивания условной регрессии, для решения которой применяются методы и свойства условного математического ожидания из теории вероятностей. Если же исследователю точно известны измерения переменной х, то используется аппарат «классической» регрессии для решения задачи определения формы и параметров модели.

В эконометрике наиболее подробно изучен частный случай простой линейной регрессии, в которой линейность означает пропорциональную зависимость y от x посредством неизвестных параметров:

(2.2)

где a₀ и a₁ – неизвестные параметры модели.

Примером модели (2.2) является модель макроэкономики, отражающая закон А. Оукена об обратной зависимости темпа роста ВНП от темпа роста уровня безработицы [3]:

где и – абсолютные приросты объема ВНП 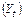и уровня безработицы за определенный период времени t. Оценки параметров по данным американской статистики составили: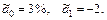

2. Модель множественной регрессии

(2.3)

где описывается зависимость одной эндогенной переменной от m(m>1) экзогенных переменных. Например, производственная функция Кобба-Дугласа в логарифмической форме принадлежит классу моделей типа (2.3):

где Y, L, K – переменные, которые обозначают объем выпуска продукции, затрачиваемого труда и основных фондов соответственно; – шоковая (возмущающая) переменная, отражающая влияние других факторов на выпуск Y.

Благодаря случайной переменной , математически описываемой случайной величиной, эндогенная переменная тоже является случайной величиной, поэтому задача восстановления зависимости y от может быть решена лишь при многократных наблюдениях этих переменных, полученных в различные моменты времени . Результаты статистических наблюдений помещают в специальную таблицу исходных данных:

Номера наблюдений (t) Наблюдаемые переменные

Эндогенная y_t Экзогенные

х₁_t … х_mt

y₁ х₁₁ … х_m₁

y₂ х₁₂ … х_m₂

Т y_T х₁_T … х_mT

Выделяются две основные задачи регрессионного анализа:

1) Установление формы взаимосвязи между переменными y и , т.е. подбор такой функции f, которая в определенном смысле оптимально характеризовала бы эту взаимосвязь.

2) Оценивание неизвестных параметров регрессионной модели, проверка гипотез об их значимости и адекватности модели анализируемому экономическому объекту.

I. Решение этих задач начнем с более простой задачи оценивания параметров простой линейной регрессии, которое без потери общности можно применить и к оценке параметров множественной линейной регрессии вида:

( )

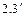В статистической науке накоплен достаточно большой арсенал методов оценивания параметров регрессии, выбор которых зависит как от степени априорной информации, доступной исследователю, так и от критерия качества, согласно которому осуществляется оптимальный выбор оценок параметров. Наиболее часто используемыми методами оценивания являются:

¨ метод максимального правдоподобия (ММП), который строит оценки, доставляющие максимум функции правдоподобия, представляющий собой функцию распределения выборочных данных, которая предусматривает знание вида закона распределения переменных модели;

¨ байесовский метод оценивания, который максимизирует апостериорную плотность распределения вероятностей переменных модели и требует еще большей информации, чем предыдущий (ММП), состоящий в знании априорного распределения вероятностей неизвестных параметров;

¨ метод моментов, который находит оценки из решения системы уравнений, составленных приравниванием выборочных и теоретических начальных моментов;

¨ метод наименьших квадратов, который минимизирует сумму квадратов отклонений реальных наблюдений за эндогенной переменной от ее значения, рассчитанных по модели.

В последнее время интенсивно развиваются робастные и непараметрические методы оценивания параметров, которые существенно уменьшают требования к наличию априорной информации о виде распределения выборочных данных и к отсутствию выбросов (аномальных наблюдений).

Основным методом решения второй задачи в эконометрике является метод наименьших квадратов (МНК), который позволяет находить оценки, обеспечивающие максимальную точность (минимальную дисперсию) в классе несмещенных и линейно связанных с наблюдениями y оценками:

(2.4)

где – подстановочное значение эндогенной переменной от включения оценок неизвестных параметров :

Тогда критерием качества оценивания по МНК будет сумма квадратов наблюдаемых отклонений реально зарегистрированных и подстановочных значений , обозначаемых символом . Этот переход делает задачу оценивания реализуемой, т.к. значения случайной переменной 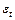– не наблюдаемые в процессе регистрации статистических данных регрессионной модели – не могут участвовать в формировании критерия качества оценивания.

Однако метод наименьших квадратов обеспечивает оптимальные свойства МНК-оценкам лишь при выполнении следующих классических модельных предположений.

П.1. Отсутствие систематических ошибок наблюдений уравнения регрессии:

Другими словами, при операции усреднения переменных моделей, влияние случайной переменной исчезает.

П.2. Наблюдения организованы так, что случайные ошибки не коррелированны между собой:

П.3. Наблюдения производятся с одинаковой точностью, т.е. дисперсии случайных переменных одинаковы во все моменты измерения:

Предположение П.3 носит название гомоскедастичности.

П.4. Экзогенные переменные измеряются без ошибок, и в случае модели множественной регрессии их значения, полученные на протяжении всех моментов наблюдения, образуют линейно-независимые векторы.

П.5. Закон распределения вероятностей случайной переменной принадлежит к классу нормальных распределений с нулевым математическим ожиданием и дисперсией которая чаще всего неизвестна.

В рамках перечисленных модельных предположений решение задачи (2.4) может быть найдено как решение системы нормальных уравнений, которая для модели простой линейной регрессии имеет вид:

(2.5)

Нетрудно получить решение системы (2.5) в явном виде:

(2.6)

где

Дадим геометрическую иллюстрацию оценки параметров, приводящей к восстановлению взаимосвязи между и по МНК:

Рис. 3

На рис.3 показано, что прямая восстановленной по МНК зависимости y от x проходит через «центр тяжести» множества обрабатываемых пар данных 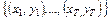. Причем, оценка 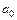определяет отрезок, отсекаемый прямой от оси ординат, а оценка представляет собой тангенс угла наклона прямой с осью абсцисс.

Перечислим важные свойства параметров простой линейной регрессии (ПЛР), полученных по МНК.

Свойство 1. Оценки параметров 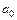и имеют нормальные вероятностные законы распределения и обладают свойством несмещенности.

Для доказательства свойства 1 представим (без потери общности) модель ПЛР в центрированном относительно переменной x виде, с этой целью введем преобразование , тогда

Тогда оценки (2.6) примут вид:

(2.7)

Заметим, что

Вследствие того, что получим:

(2.8)

и (после усреднения оператором математического ожидания) окончательно будем иметь:

(2.9)

Соотношение (2.9) указывает на несмещенность

Вычислим дисперсию этой оценки:

Окончательно учитывая аддитивность нормального распределения и связь (2.8) между случайными величинами и 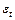, замечаем, что оценки имеют нормальный закон распределения вероятностей со средним 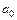, дисперсией . Однако на практике дисперсия случайной переменной – обычно неизвестна и ее заменяют несмещенной оценкой вида (величину s именуют SEE):

(2.10)

С учетом формулы (2.10) нетрудно определить доверительный интервал параметра 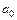на основании известного из теории вероятностей факта, что величина следует закону распределения Стьюдента с параметром Т–2, который соответствует числу степеней свободы, содержащемуся в исходных данных. В нашем случае (ПЛР) исходные данные связаны двумя параметрическими зависимостями, поэтому независимых данных насчитывается Т–2. Тогда, задавая доверительную вероятность и определяя по таблицам закона Стьюдента квантиль из условия получим доверительный интервал для параметра :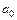

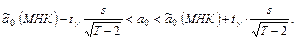(2.11)

Проведем анализ вероятностных свойств оценки параметра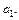

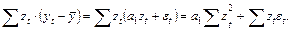
Отсюда

(2.12)

Подвергая равенство (2.12) оператору усреднения, получим:

что подтверждает несмещенность оценки .

Вычисляя дисперсию оценки , будем иметь:

.

Тогда можно сделать вывод о нормальности вероятностного распределения оценки со средним и дисперсией

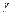Доверительный интервал для параметра с надежностью при неизвестной дисперсии имеет вид:

.

Свойство 2. Фундаментальное свойство МНК формулируется в виде теоремы Гаусса-Маркова, отмечающей высокую степень близости МНК-оценок к искомым параметрам.