 |
Главная |
Необходимое условие устойчивости
|
из
5.00
|
Таким условием является положительность всех коэффициентов характеристического уравнения (6.5). В этом можно убедиться, если при известных корнях  представить характеристический полином
представить характеристический полином  в виде произведения
в виде произведения 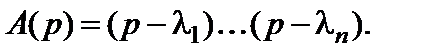
В случае, когда все корни  , вещественные
, вещественные  , характеристическое уравнение принимает вид
, характеристическое уравнение принимает вид 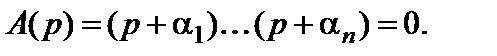
Раскрывая скобки, получим уравнение типа (6.5), где все коэффициенты  будут положительными. Можно убедиться в том, что аналогичный результат получится, если корни
будут положительными. Можно убедиться в том, что аналогичный результат получится, если корни 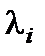 комплексно-сопряженные с отрицательной вещественной частью.
комплексно-сопряженные с отрицательной вещественной частью.
Таким образом, коэффициенты характеристического уравнения (6.5) устойчивой системы всегда будут положительны. При наличии хотя бы одного отрицательного коэффициента система будет неустойчива, дополнительных исследований не требуется.
В то же время следует помнить, что положительность всех коэффициентов характеристического уравнения еще не гарантирует устойчивости системы, необходима ее дополнительная проверка.
В ТАУ основным инженерным методом решения дифференциальных уравнений, т. е. исследования поведения систем во времени, является преобразование Лапласа. Его преимущество заключается в том, что операции дифференцирования и интегрирования оно заменяет более простыми алгебраическими операциями умножения и деления. Из-за необходимости вычислять корни характеристического уравнения преобразование Лапласа целесообразно использовать лишь для систем до четвертого порядка, решать ОДУ более высокого порядка удобнее численными методами на ЭВМ.
Рассмотрим принцип решения дифференциальных уравнений с помощью преобразования Лапласа. На первом этапе производят прямое преобразование X(s) = L{x(t)} – от функции времени переходят к функции комплексной переменной Лапласаs = σ + jω = α + jβ. Здесь ω = 2πf – это известная из электротехники круговая частота, рад/с. Далее решают алгебраическое уравнение реакции, для чего находят собственные значения системы, т. е. корни характеристического уравнения D(s) = 0, и по теореме разложения определяют коэффициенты числителей простых дробей, на которые в соответствии с собственными значениями разлагается реакция. В конце вычислений выполняют обратное преобразование Лапласа x(t) = L-1{X(s)} – от функции переменной s возвращаются к функции переменной t.
Общее обозначение описанных операций x(t)÷X(s), где слева строчными буквами изображена функция времени (оригинал), справа, прописной буквой – функция комплексного переменного (изображение), а между ними стоит символ соответствия (ни в коем случае не равенства, что будет являться грубой ошибкой!). Практически все функции электротехники и ТАУ соответствуют требованиям к оригиналу (функция кусочно-непрерывна на участке исследования, равна нулю при t< 0 и ограничена функцией 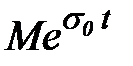 , где σ0 – абсцисса абсолютной сходимости).
, где σ0 – абсцисса абсолютной сходимости).
Иногда для обозначения оператора дифференцирования p ≡ d/dt и комплексной переменной s = σ + jω = α + jβ используют один и тот же символ p, что может приводить к недоразумениям или неправильным результатам. Мы будем далее использовать отдельные обозначения.
Приведем без доказательств свойства преобразования Лапласа.
- Линейностьx(t) + y(t) ÷ X(s) + Y(s).
- Однородностьkx(t) ÷ kX(s).
- Подобие  .
.
- Дифференцирование оригинала
| Полином, отражающий начальные условия |
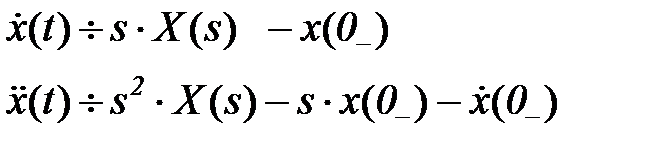
При нулевых начальных условиях (значениях переменных в момент t= 0-, уже существующих в системе) запись упрощается
 .
.
Дифференцированию оригинала соответствует умножение его изображения на s в степени, равной порядку дифференцирования (производной).
- Интегрирование оригинала
| Учет начальных условий |

При нулевых начальных условиях запись упрощается (интегрированию оригинала соответствует деление его изображения на s)
 .
.
- Запаздывание (смещение) оригинала во времени на величину τ > 0
 .
.
- Смещение изображения на комплексной плоскости на величину λ
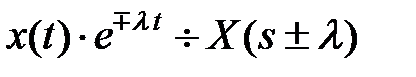 .
.
- Начальное значение оригинала (при t = 0+), вычисляемое (обратите внимание на то, что в выражении использован знак равенства, а не соответствия)
 .
.
Для вычисления начального значения производной по времени от функции x(t)n-го порядка производится умножение изображения на sn+1
 .
.
Пример: определим начальные значения функции F(s) и ее производной
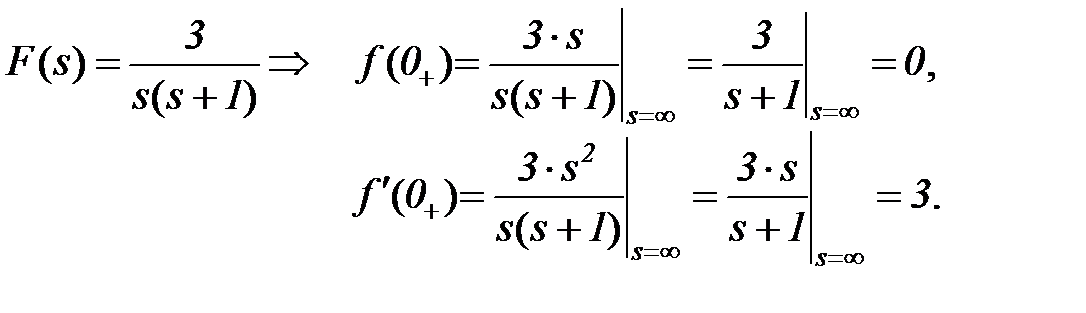
При подстановке значения переменной s, равного бесконечности, раскрытие неопределенности производится по правилу Лопиталя, которое, применительно к данному случаю, можно сформулировать следующим образом. Если максимальная степень, в которую возводится бесконечное число в числителе, больше аналогичной в знаменателе, то все выражение стремится к бесконечности (не забывать про знак!), если меньше, то стремится к нулю. Если максимальные степени бесконечных чисел в числителе и знаменателе дроби равны, то все выражение равно отношению коэффициентов при бесконечных величинах.
- Конечное значение оригинала (при t = ∞), также вычисляется с использованием знака равенства, а не соответствия
 .
.
Пример:  .
.
Прямое
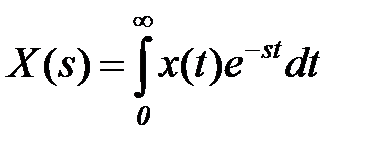
и обратное
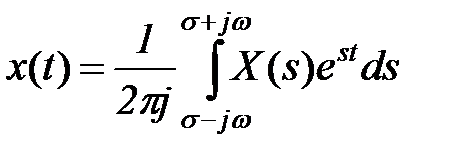
преобразования Лапласа являются интегральными, т.е. достаточно сложными для вычисления. Однако, учитывая ограниченное количество используемых функций, в инженерной практике используют вместо них готовые таблицы соответствия оригиналов и изображений (таблица 6.1).
Таблица 6.1
| Изображение X(s) | Оригинал x(t) | |

| импульсная функция k∙δ(t) | |
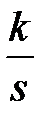
| – простой нулевой корень | скачок k∙1(t) или просто k |
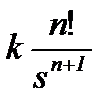
| – кратный нулевой корень | k∙tn – степенной ряд от t |

| – простой действительный корень | 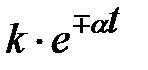 – экспонента – экспонента
|

| – кратный действительный корень |  , при n > 1 , при n > 1
|

| – сопряженные мнимые корни | k∙sinωt – гармоническая функция |

| – сопряженные мнимые корни | k∙cosωt – гармоническая функция |
сопряженные комплексные корни
 , объединенные в одну дробь , объединенные в одну дробь
 ,
с вычислением ,
с вычислением 
| а) предпочтительная форма
 б) через синус
б) через синус
 в) через косинус
в) через косинус

| |
сопряженные комплексные корни
(раздельное представление)

| 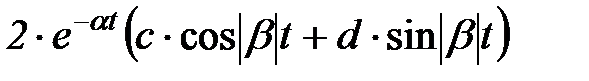 перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), и минус в противном случае
перед d ставят плюс, если знаки мнимых частей изображения в числителе и знаменателе совпадают (как показано), и минус в противном случае
|
Примечание – Даже если скачок 1(t) в формуле для входной функции не пишется, то всегда подразумевается, т.к. по Лапласу при t = 0- любая функция f(t) равна нулю, а затем она появляется скачком. Однако сомножитель 1/s вводят в изображение входной функции лишь в том случае, если она представляет собой чисто ступенчатое воздействие, даже если в функциях-оригиналах другого вида скачок и был указан.
Передаточная функция
Операторная передаточная функция W(s) является основной формой описания систем в операторной области по методу один вход, один выход.
Она может быть получена:
- по структурной схеме (методы эквивалентных преобразований были рассмотрены нами ранее);
- по дифференциальному уравнению – заменяя операцию дифференцирования переменной s, функции времени их изображениями по Лапласу и считая начальные условия нулевыми, получаем из ОДУ
(a0 sn + a1 sn-1 + ... + an ) Y(s) = (b0 sm + b1 sm-1 + ... + bm) X(s),
 .
.
Отношение изображений по Лапласу выходной величины к входной при нулевых начальных условиях называется передаточной функцией.
Для реальных систем m ≤ n, поэтому передаточная функция обычно представляет собой правильную рациональную дробь.
Корни характеристического уравнения
D(s) = a0sn + a1sn-1 + ... + an = 0
характеризуют собственные свойства системы и дают решение однородного дифференциального уравнения без правой части, т. е. описывают свободное движение автономной системы.
Функция 1/D(s) называется системной, функция N(s) – возбуждающей.
С точностью до коэффициента b0/a0 ПФ может быть выражена корнями полинома числителя (нулями) и полинома знаменателя (полюсами)
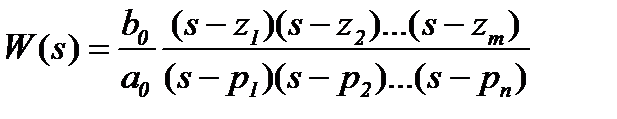 .
.
На комплексной плоскости нули обозначают кружком, а полюса – крестиком.
Поскольку и числитель, и знаменатель представляют собой алгебраические многочлены с действительными коэффициентами, комплексные корни могут быть только сопряженными, т.е. образовывать пары с положительной и отрицательной мнимыми частями. Число корней равно степени многочлена.
Как правило, ПФ приводят к стандартному виду (нормируют), приравнивая к единице старший коэффициент при s, либо свободный член полиномов.
Нормирование по старшему коэффициенту вида
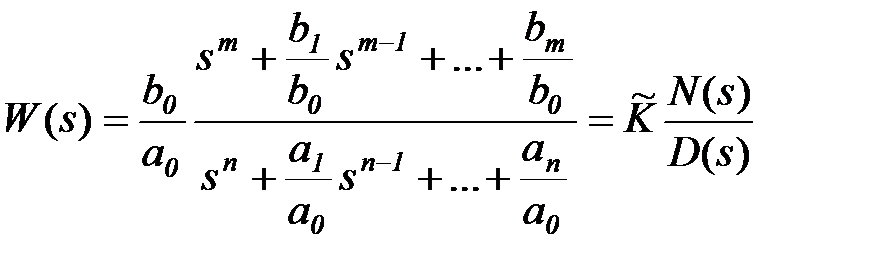
обычно применяется при работе с корнями или при переходе к описанию системы в пространстве состояний.
Нормирование по свободному члену

используется при работе с типовыми динамическими звеньями.
Число перед дробью (общий множитель) называется коэффициентом передачи в общем случае и коэффициентом усиления (Gain), если параметры входа/выхода безразмерны или имеют одинаковую размерность.  иk в общем случае не равны. Коэффициент k = bm/an, обозначаемый также kуст или k(∞), называется коэффициентом усиления системы в установившемся режиме.
иk в общем случае не равны. Коэффициент k = bm/an, обозначаемый также kуст или k(∞), называется коэффициентом усиления системы в установившемся режиме.
ИзW(s) = Y(s)/X(s) следуетY(s) = X(s)∙W(s). Иначе говоря, изображениереакции системы на любое воздействие, имеющее изображение по Лапласу, может быть определено как произведение последнего на передаточную функцию системы.
Вид W(s) и W(p) схож лишь при нулевых начальных условиях и только для стационарных систем.
Если звено (система) является стационарным, т.е. описывается ОДУ с постоянными коэффициентами, то имеет место сходство между передаточными функциями в форме изображения Лапласа W(s) и в операторной форме W(p). Чтобы перейти от одной формы к другой, достаточно сделать подстановку p = s и наоборот. Однако для нестационарных звеньев эта операция не допускается, для них возможна только форма W(p, t). При ненулевых начальных условиях отличается функция W(s, x0), в которой появляются элементы учета начальных значений переменных при t = 0, которых нет в W(p).
Решение уравнений движения системы
Для решения дифференциального уравнения с помощью преобразования Лапласа необходимо:
- найти корни характеристического уравнения  ;
;
- найти изображение реакции Y(s) и записать его в виде суммы простых дробей по теореме разложения в соответствии с полюсами;
- найти коэффициенты числителей каждой дроби (вычеты в полюсах);
- найти оригинал для каждой дроби по таблице соответствия и записать конечное решение в виде суммы отдельных оригиналов.
При этом целесообразно учитывать следующие рекомендации:
а) перед вычислением корней знаменатель обязательно следует нормировать по старшему коэффициенту при s, иначе может возникнуть типичная ошибка (в примере потерян коэффициент 0,5 при s2, на самом деле после преобразования должно быть 10/(s+1)/(s+2))
 !
!
б) нельзя сокращать существующие нули и полюсы с положительной действительной частью, ведущие к неустойчивости системы, если их части не являются целыми числами; остальные нули и полюса могут быть сокращены перед переходом во временную область;
в) для кратных полюсов записывают дробями все степени корня от наибольшей до первой в порядке их убывания;
г) комплексные сопряженные корни записывают, как правило, в виде одной общей дроби.
После разложения на простые дроби и вычисления вычетов полезно проверить правильность результата. Первое правило проверки – сумма дробей правой части должна быть равна изображению в левой части равенства. Второе правило проверки – сумма всех составляющих оригинала при t = 0 (начальное значение оригинала) в соответствии со свойствами преобразования Лапласа должна быть равна  .
.
В общем случае реакция системы состоит из вынужденной и свободной составляющих y(t)=yвын(t)+yсв(t), изображения которых имеют одинаковый знаменатель (характеристический полином системы)
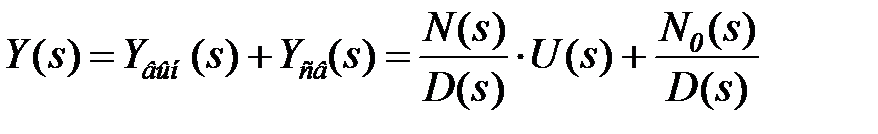 .
.
Вынужденная составляющая yвын(t) является реакцией системы на входное воздействие при нулевых начальных условиях y(0_) = 0. Свободная составляющая yсв(t) или переходный процесс автономной системы является решением однородного дифференциального уравнения (без правой части) и определяется начальными условиями.
Используют два способа вычисления совокупного переходного процесса. В первом случае система обычно задается ОДУ, производят индивидуальное преобразование каждого члена дифференциального уравнения, вычисляются одновременно вынужденная и свободная составляющие.
По второму способу выполняют независимое вычисление вынужденной и/или свободной составляющих, при этом система обычно задана ПФ или структурной схемой. Для вычисления N0(s) по D(s) используется формула (схожая, но не равная вычислению производной)

Если рассчитывается полное движение системы с учетом ненулевых начальных условий, запрещается производить сокращения в левой части ОДУ (в характеристическом полиноме D(s) системы). Обусловлено это требование тем, что именно вид характеристического полинома определяет свободную составляющую переходного процесса, т.е. реакцию на начальные условия.
Если начальные условия не заданы, то по умолчанию они считаются нулевыми.
Варианты заданий.
Вариант № 1
а)  ; б)
; б)  ;
;
Вариант № 2
а) 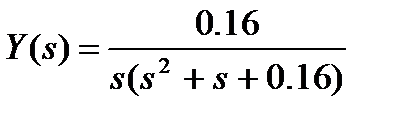 ; б)
; б)  .
.
Вариант № 3
а)  ; б)
; б)  ;
;
Вариант № 4
а) 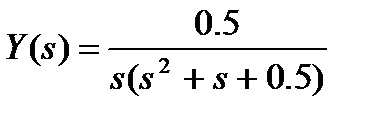 ; б)
; б)  .
.
Вариант № 5
а)  ; б)
; б)  ;
;
Вариант № 6
а)  ; б)
; б)  .
.
Вариант № 7
а) 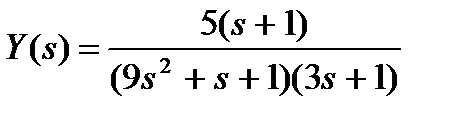 ; б)
; б) 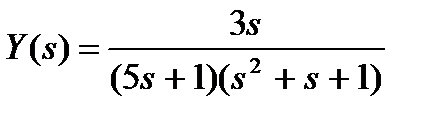 ;
;
Вариант № 8
а)  ; б)
; б) 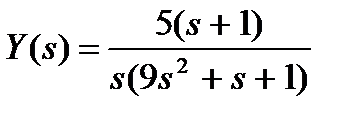 .
.
Вариант № 9
а)  ; б)
; б)  ;
;
Вариант № 10
а)  ; б)
; б)  .
.
Вариант № 11
а)  ; б)
; б) 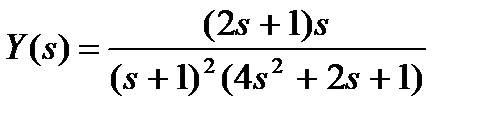 ;
;
Вариант № 12
а) 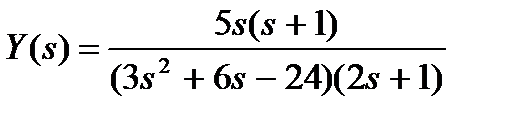 ; б)
; б)  .
.
Вариант № 13
а)  ; б)
; б) 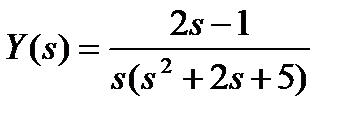 ;
;
Вариант № 14
а)  ; б)
; б) 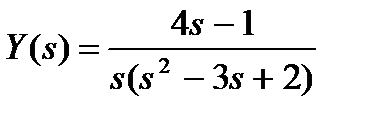 .
.
Вариант № 15
а)  ; б)
; б)  ;
;
Вариант № 16
а)  ; б)
; б) 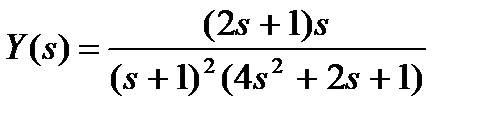 .
.
Вариант № 17
а) 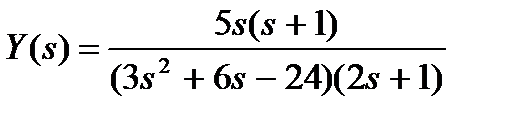 ; б)
; б)  ;
;
Вариант № 18
а)  ; б)
; б)  .
.
Вариант № 19
а)  ; б)
; б)  ;
;
Вариант № 20
а)  ; б)
; б) 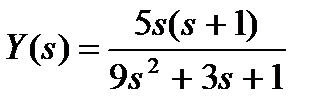 .
.
Вариант № 21
а)  ; б)
; б)  ;
;
Вариант № 22
а) 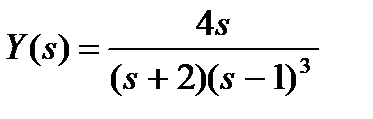 ; б)
; б)  .
.
Вариант № 23
а)  ; б)
; б) 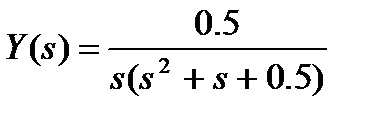 ;
;
Вариант № 24
а)  ; б)
; б)  .
.
Приложение А
(справочное)
|
из
5.00
|
Обсуждение в статье: Необходимое условие устойчивости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

