 |
Главная |
Критерий Льенара-Шипара
|
из
5.00
|
Критерий Льенара-Шипара. При  удобнее применять одну из модификаций критерия Гурвица, называемую критерием устойчивости Льенара-Шипара (1914 г.), который проще и требует раскрытия меньшего числа определителей, чем критерий Гурвица. Число условий устойчивости при его применении существенно снижается. По этому критерию САУ устойчива, если при
удобнее применять одну из модификаций критерия Гурвица, называемую критерием устойчивости Льенара-Шипара (1914 г.), который проще и требует раскрытия меньшего числа определителей, чем критерий Гурвица. Число условий устойчивости при его применении существенно снижается. По этому критерию САУ устойчива, если при  только
только 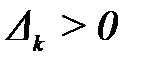 или
или  , где
, где 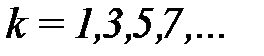 . Например, при
. Например, при  ,
,  САУ устойчива, если
САУ устойчива, если  (обычно
(обычно  ).
).
Задание:
Ø Задание 7.1
С помощью алгебраического критерия Гурвица, Льенара-Шипара определить устойчивость линейной системы автоматического управления со следующей структурной схемой (обратная связь отрицательная):
при K = 10; Т1= 0,5с; Т2= 0,5с; Т3= 0,07с; Т4= 0,01с.
Ø Задание 7.2
Выполнить приведенное выше задание 7.2 при следующих параметрах САУ: K = 1000, Т1= 0,5с, Т2= 0,1с, Т3= 0,02с, Т4= 0,01с.
Ø Задание 7.3
Выполнить приведенное выше задание 7.1 при условии, что в структурной схеме САУ обратная связь положительная.
Ø Задание 7.4
С помощью алгебраического критерия Гурвица определить устойчивость линейной системы автоматического управления со следующей структурной схемой:
при K = 100; Т = 0,1с; ξ = 0,3.
Ø Задание 7.5
С помощью алгебраического критерия Рауса, Льенара-Шипара определить устойчивость линейной системы автоматического управления со следующей структурной схемой:
при K = 100; Т = 0,1с; ξ = 0,3.
Ø Задание 7.6
С помощью алгебраического критерия Гурвица, Льенара-Шипара определить устойчивость линейной системы автоматического управления со следующей структурной схемой:
при K = 10; Т1= 0,1с; ξ = 0,3; T2= 1; T3= 0,5.
Ø Задание 7.7
С помощью алгебраического критерия Гурвица, Льенара-Шипара определить устойчивость линейной системы автоматического управления со следующей структурной схемой:
при K1= 100; Т1= 0,5с; ξ 1= 0,05; Т2= 0,2с; Т3= 0,001с; ξ3= 0,5; K2 = 100; Т4= 0,05.
Ø Задание 7.8
С помощью алгебраического критерия Рауса, Льенара-Шипара определить устойчивость линейной системы автоматического управления со следующей структурной схемой:
при K1= 10; T1= 0,1с; ξ 1= 0,3; T2 = 1; K2= 50; T3= 0,5; ξ 3= 0,03; Т4= 0,5; Т5= 0,01.
Ø Задание 7.9
С помощью алгебраического критерия Рауса, Льенара-Шипара определить устойчивость линейной системы автоматического управления со структурной схемой, приведенной в задании 7.1 , при следующих условиях:
W1= p; W2= 100/(0,5p+1); W3= W4= W5= 1/(p2+p+1); W6= W7= 1/p.
Указания по выполнению работы:
Пример 7.1 С помощью алгебраического критерия Гурвица определим устойчивость линейной системы автоматического управления со следующей структурной схемой (обратная связь отрицательная):
при K = 10; Т1= 0,5с; Т2= 0,1с; Т3= 0,02с; Т4= 0,01с.
Решение
| № п/п | Алгоритм | Конкретное соответствие данной ситуации предложенному алгоритму |
| Записать характеристическое уравнение САУ. | Определяем характеристический полином: D(p) = T1T3T4p4 + (T1T3 + T1T4 + T3T4)p3 + + (T1 + T3 + T4)p2 + (KT2+1)p +K. Подставляя значения параметров САУ и приравнивая полином к нулю, получаем характеристическое уравнение D(l) = a4l4 + a3l3 + a2l2 + a1l + a0 = 0 где a4 = 0,0001, a3 = 0,0152, a2 = 0,521, a1 = 2, a0 = 10. | |
| Проверить выполнение необходимых условий устойчивости. | Все коэффициенты характеристического уравнения положительны – основное необходимое условие выполнено.
Рассчитываем показатели дополнительного необходимого условия устойчивости:
 Значения М1и М2 меньше 1 – дополнительное необходимое условие устойчивости выполнено.
Значения М1и М2 меньше 1 – дополнительное необходимое условие устойчивости выполнено.
| |
| Вычислить соответствующие характеристики алгебраических критериев. | Вычисляем значения определителя Гурвица и его диагональных миноров в безразмерной форме:

| |
| Произвести проверку выполнения условий устойчивости. | Старший безразмерный определитель Гурвица и его диагональные миноры больше нуля – исследуемая система устойчива. |
Пример 7.2 Определим устойчивость системы с помощью алгебраического критерия Гурвица.
Уравнение непрерывной части системы описывается уравнением (1).
Объект управления (ОУ) описывается линейным дифференциальным уравнением третьего порядка:

(1)
Пусть Т1 = 8, Т2 = 12, Т3 = 5, k = 3. Коэффициент Тn = 0.175 в первой контрольной работе не используется. Уравнение (1) примет вид:
 (2)
(2)
Передаточная функция ОУ в общем случае может быть представлена в виде отношения
 ,
,
где  и
и  – изображения по Лапласу выходной и входной переменных ОУ, соответствующих левой и правой частям уравнения 1. Отсюда, передаточная функция будет иметь вид:
– изображения по Лапласу выходной и входной переменных ОУ, соответствующих левой и правой частям уравнения 1. Отсюда, передаточная функция будет иметь вид:
 , (3)
, (3)
или
 . (4)
. (4)
Воспользуемся алгебраическим критерием устойчивости Рауса-Гурвица в форме Гурвица.
Рассмотрим характеристический полином передаточной функции системы  .
.
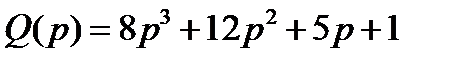 .
.
Из коэффициентов характеристического полинома составим матрицу:
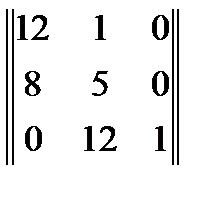
Критерий устойчивости Гурвица сводится к тому, что должны быть больше нуля все диагональные миноры данной матрицы.
Проверим:
 , первый минор положителен;
, первый минор положителен;
 , второй минор положителен.
, второй минор положителен.
Так как в последнем столбце матрицы Гурвица все элементы, кроме нижнего, равны нулю, то последний определитель выражается через предпоследний следующим образом:
 , третий определитель также положителен.
, третий определитель также положителен.
Следовательно, в разомкнутом состоянии система устойчива.
Используем критерий Гурвица для системы в замкнутом состоянии. Передаточная функция (ПФ) замкнутой системы по отношению к разомкнутой ПФ представляется выражением:
 . (5)
. (5)
Отсюда,
 .
.
Также как и для разомкнутой системы, составим матрицу из коэффициентов характеристического полинома ПФ.
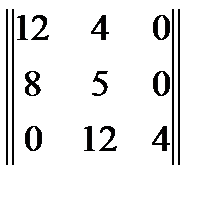
Проверим знак всех диагональных миноров.
 , первый минор положителен;
, первый минор положителен;
 , второй минор положителен. Третий минор
, второй минор положителен. Третий минор  . Непрерывная часть в замкнутом состоянии устойчива.
. Непрерывная часть в замкнутом состоянии устойчива.
Пример 7.3 Расчет устойчивости систем по критерию Гурвица.
Рассчитать устойчивость системы, заданной следующей структурной схемой (рис 7.3)

Рисунок 7.3
W1(P)=k1; W2(P)=  ;W3(P)=
;W3(P)= 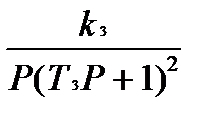 ; W4(P)=
; W4(P)=  .
.
Параметры звеньев: k1=12; k2=80; k3=0.15; k4=2; T2=0.5; T3=10; T4=2.
Запишем эквивалентную передаточную функцию системы
Wзам(р) =  .
.
Запишем передаточную функцию системы, разомкнутой по главной обратной связи.
Wраз(p) = W1(P) ×W2(P) ×W3(P) ×W4(P) = 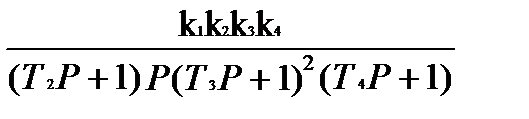 .
.
Характеристическое уравнение системы.
D(p)=1+ Wраз(p)=0 ® D(p)=1+ 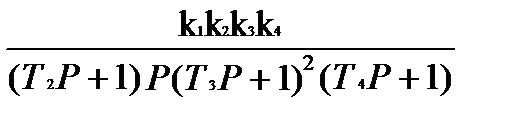 = 0;
= 0;
Kэ+(Т2Т3р3+Т2р2+Т4р+р)(Т32р2+2Т3р+1)=0; Kэ=К1К2К3К4;
Kэ + Т2Т4Т32 р5 + (2Т2Т4Т3 + Т2Т32 + Т4Т32) р4 + (Т4Т2 + 2Т2Т3 + 2Т4Т3 + Т32) р3 +
(Т2 + Т4 + 2Т3) р2 + р = 0 ®  .
.
Подставляя численные значения, получаем:
 .
.
Т.к. все коэффициенты положительны, то первое условие Гурвица выполняется.
Составим матрицу из коэффициентов характеристического уравнения и вычислим определители:
| 22.5 | |||
| 22.5 | |||
D1=270>0; D2=270•151-100•22,5=38520>0
| 22.5 | ||||
| D3= | = 917325+0+7776000-0-72900-50625 = 8569800>0 | |||
| 22.5 |
| 22.5 | |||||
| D4 = | = – 7 ,96*108 <0 | ||||
| 22.5 | |||||
Т.к. D4 меньше нуля то система неустойчива.
Критерий Рауса. Коэффициенты первого столбца таблицы должны быть положительны.
100р5+270р4+151 р3+ 22,5р4+ р+288=0
| № п/п | Значение вспомогательного коэффициента | Столбец 1 | Столбец 2 | Столбец 3 |
| ---------------- | 
| 
| 
| |
| ---------------- | 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| ||

| 
|
Т.к. с15<0, то система неустойчива.
|
из
5.00
|
Обсуждение в статье: Критерий Льенара-Шипара |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

