 |
Главная |
Преобразования Лоренца
|
из
5.00
|
В релятивистской механике преобразования координат Галилея заменяются на преобразования координат Лоренца.
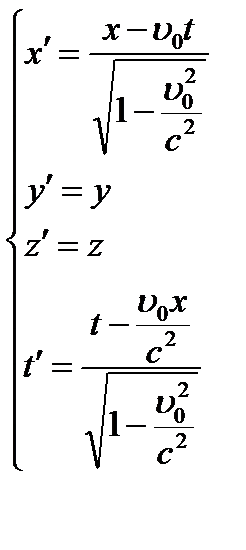
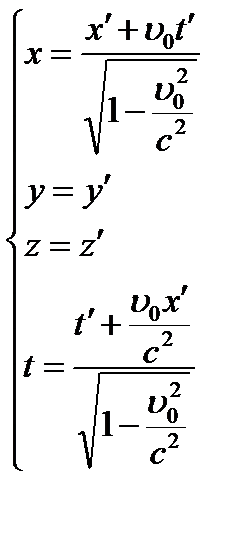
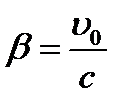
Иногда для упрощения записи вводятрелятивистский множитель:
Если u0 << c (b << 1), то преобразования Лоренца переходят в преобразования Галилея.
Из преобразований Лоренца можно получить ряд следствий.
22.Следствия из преобразования Лоренца.
Относительность одновременности событий.
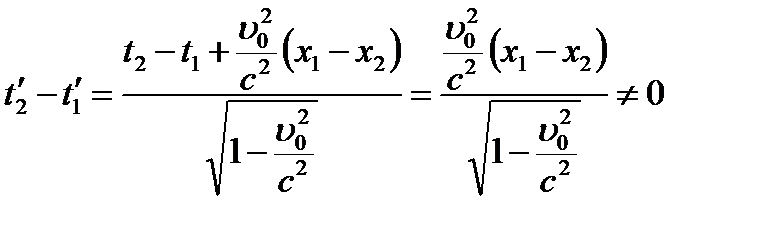
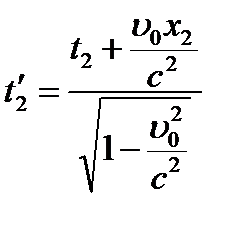
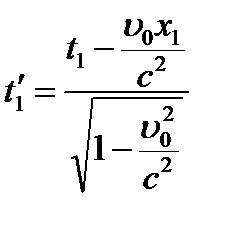 Пусть в системе K в двух разных точках с координатами x1 и x2 (x1 ¹ x2) в один и тот же момент времени (t1 = t2) происходят два события.
Пусть в системе K в двух разных точках с координатами x1 и x2 (x1 ¹ x2) в один и тот же момент времени (t1 = t2) происходят два события.
События, одновременные в системе К, в системе К¢ оказываются неодновременными, т. е. одновременность событий – относительна.
Вывод:Время – неинвариантная величина.
Релятивистское изменение длины.
Пусть в системе K¢ покоится стержень длинойl0 = x2¢ - x1¢ (собственная длина тела).
Длина стержня в системе K равнаl = x2 - x1, где x1 и x2 – координаты концов стержня в системе K, измеренные в один и тот же момент времени (t1 = t2).
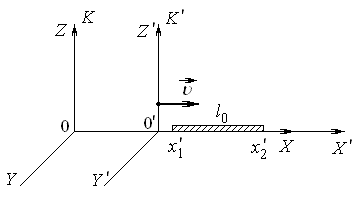
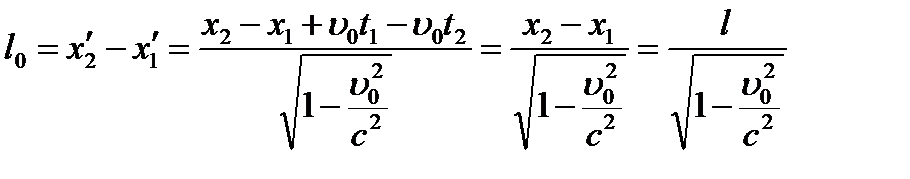
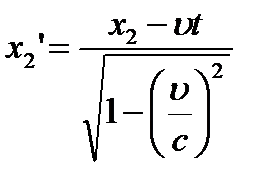
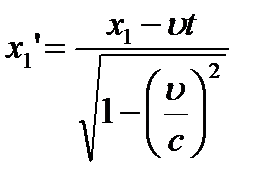 Используем прямые преобразования координат:
Используем прямые преобразования координат:
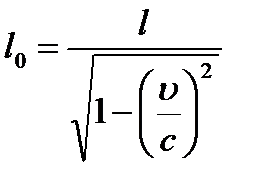
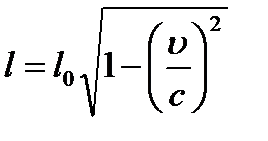
Это и есть релятивистское изменение длины:
Его также называют лоренцевым сокращением длины.
Размеры тела относительно неподвижной СО сокращаются только в направлении движения относительно неподвижной системы отсчета.
а) тела неподвижные;
б) тела движутся со скоростью u.
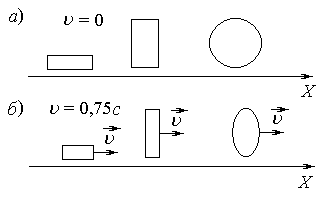
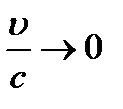
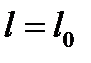 Следствия:
Следствия:
1) 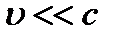 , то и - классическая физика.
, то и - классическая физика.
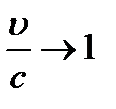
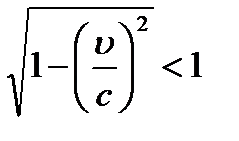
2) 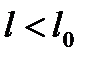
 , то и , тогда
, то и , тогда
Вывод:Линейные размеры тела максимальны в той ИСО, относительно которой тело покоится.
Промежуток времени между события (длительность событий)
Пусть в системе К¢ в одной и той же точке (х2¢=х1¢=х¢) происходит некое событие длительностью t¢ = t2¢ - t1¢.
t¢ - собственное время
Найдем длительность t этого события в системе K:
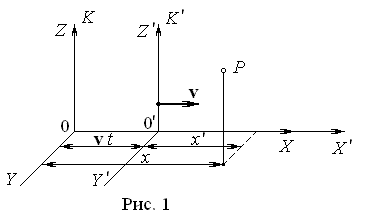
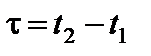 Используем обратные преобразования времени.
Используем обратные преобразования времени.
Релятивистское изменение промежутков времени.
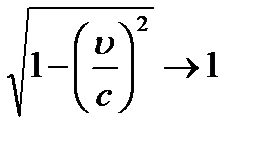
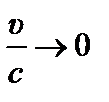 Вывод:
Вывод:
1) 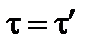
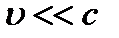 И , то , тогда - классическая физика
И , то , тогда - классическая физика
2) 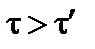
 И чем больше скорость u, тем
И чем больше скорость u, тем
Неподвижному наблюдателю процессы в движущейся СО кажутся замедленными.
23.Релятивистский закон сложения скоростей.
Релятивистский закон сложения скоростей.
Запишем преобразования Лоренца в дифференциалах:
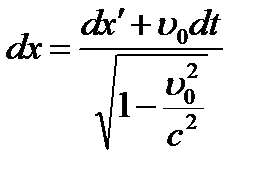
dy = dy¢
dz = dz¢
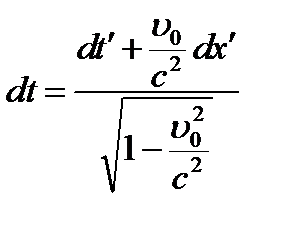
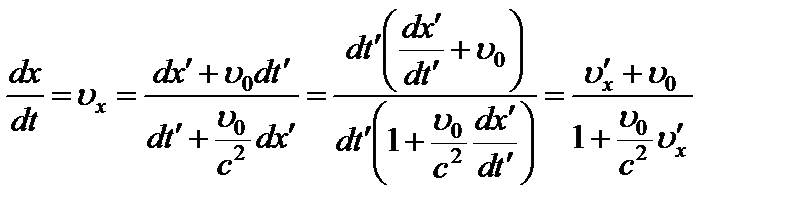 Разделим dx, dy и dz на dt:
Разделим dx, dy и dz на dt:
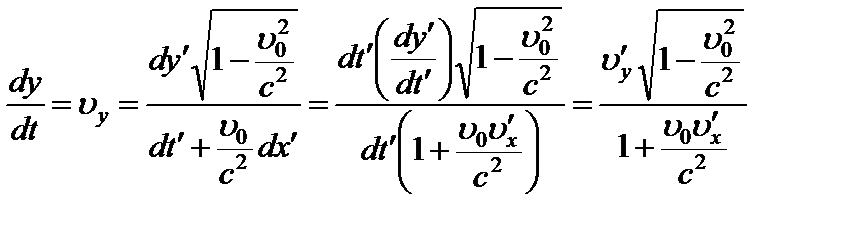
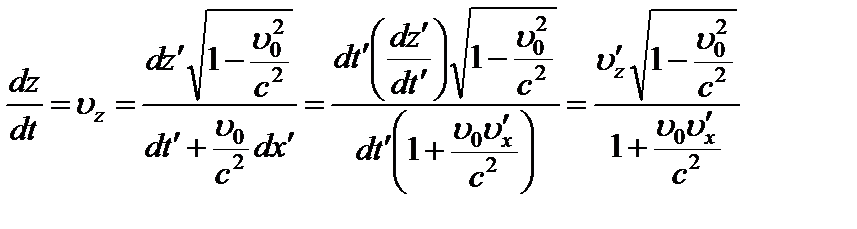
Получаем:
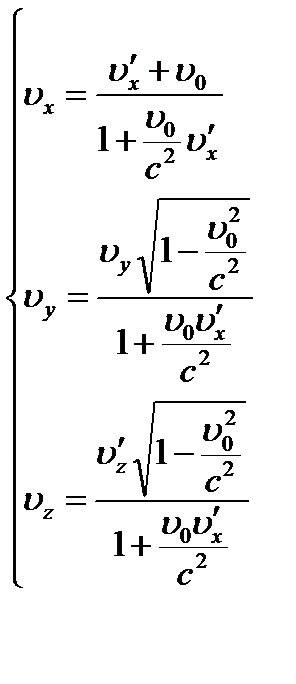 Релятивистская теорема о сложении скоростей:
Релятивистская теорема о сложении скоростей:
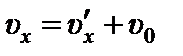
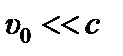 Следствия:
Следствия:
1)Если , тогда получаем - классический закон сложения скоростей
2)Пусть частица (фотон, нейтрино) движется в СО К¢ со скоростью
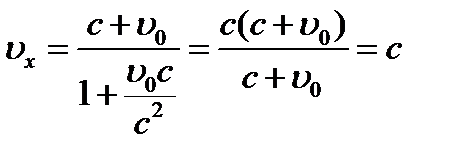
Если частица движется относительно ИСО со скоростью света с, то относительно любой другой ИСО она также движется со скоростью с, что подтверждает 2-ой постулат СТО.
24.Релятивистская динамика.
|
из
5.00
|
Обсуждение в статье: Преобразования Лоренца |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

