 |
Главная |
Окончание приложения 6
|
из
5.00
|
| Уровень значимости a = 0,05 | ||||||||||||
 К1
К2 К1
К2
| ||||||||||||
| 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,36 | 19,37 | 19,38 | 19,39 | 19,40 | 19,41 | |
| 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,88 | 8,84 | 8,81 | 8,78 | 8,76 | 8,74 | |
| 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | 5,96 | 5,93 | 5,91 | |
| 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,78 | 4,74 | 4,70 | 4,68 | |
| 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | 4,06 | 4,03 | 4,00 | |
| 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | 3,63 | 3,60 | 3,57 | |
| 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | 3,34 | 3,31 | 3,28 | |
| 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,13 | 3,10 | 3,07 | |
| 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,97 | 2,94 | 2,91 | |
| 4,84 | 3,98 | 3,59 | 3,36 | 3,20 | 3,09 | 3,01 | 2,95 | 2,90 | 2,86 | 2,82 | 2,79 | |
| 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3,00 | 2,92 | 2,85 | 2,80 | 2,76 | 2,72 | 2,69 | |
| 4,67 | 3,80 | 3,41 | 3,18 | 3,02 | 2,92 | 2,84 | 2,77 | 2,72 | 2,67 | 2,63 | 2,60 | |
| 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,70 | 2,65 | 2,60 | 2,56 | 2,53 | |
| 4,54 | 3,68 | 3,29 | 3,06 | 2,90 | 2,79 | 2,70 | 2,64 | 2,59 | 2,55 | 2,51 | 2,48 | |
| 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | 2,49 | 2,45 | 2,42 | |
| 4,45 | 3,59 | 3,20 | 2,96 | 2,81 | 2,70 | 2,62 | 2,55 | 2,50 | 2,45 | 2,41 | 2,38 | |
Параметрические критерии значимости
Нулевая
гипотеза H 
| Дополнительные условия | Критерий проверки  (критериальная
статистика)
(критериальная
статистика)
| Используемое распределение | Конкур гип.
H 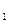
| Критическая область и формулы для нахождения её границ | Гипотеза H  не отвергается,
если не отвергается,
если
| |
 : : 
|
 известно
известно
|  U
U 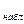 = = 
| Нормальный закон Функция Лапласа |  > > 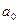
| ПКО |  
|

|
 < < 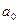
| ЛКО | ||||||
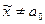
| ДКО | 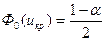
| |||||

|
 неизвестно
неизвестно
|

| Стьюдента с  степенями свободы
степенями свободы
| 
| ПКО | 
| 
|

| ЛКО | 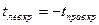
| 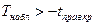
| ||||
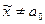
| ДКО | 
| 
| ||||
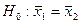
|

| 
| Нормальный закон Функция Лапласа | 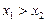
| ПКО | 
| 
|

| ЛКО | 
| |||||

| ДКО | 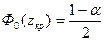
| 
| ||||
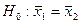
|  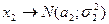 
| 
| Стьюдента с  степенями свободы степенями свободы
| 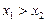
| ПКО | 
| 
|

| ЛКО | 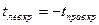
| 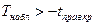
| ||||

| ДКО | 
| 
| ||||
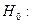 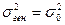
|

|

| 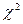 распред. с распред. с
 степенями свободы
степенями свободы
| 
| ПКО | 
| 
|

| ЛКО | 
| 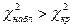
| ||||
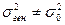
| ДКО | 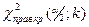

| 
|
Нулевая
гипотеза H 
| Дополнительные условия | Критерий проверки  (критериальная
статистика)
(критериальная
статистика)
| Используемое распределение | Конкур гип.
H 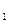
| Критическая область и формулы для нахождения её границ | Гипотеза H  не отвергается,
если не отвергается,
если
| |

|
 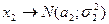
|
 
| F распред. с

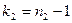 степенями свободы
степенями свободы
|
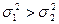
| ПКО |

|

|

| ДКО |
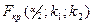
|

| ||||

|

 неизвестна неизвестна
| 

| Нормальный закон Функция Лапласа | 
| ПКО |  
| 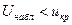
|

| ЛКО | 
| |||||

| ДКО | 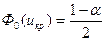
| 
| ||||

|

| 
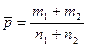


| Нормальный закон Функция Лапласа |

| ПКО |
 
|
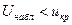
|

| ЛКО |

| |||||

| ДКО |
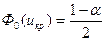
|

|
| СОДЕРЖАНИЕ | |
| 1. Элементы комбинаторики………………………………………………… | |
| 1.1. Размещения………………………………………………………………… | |
| 1.2 Понятие факториала……………………………………………………….. | |
| 1.3 Размещения с повторениями……………………………………………… | |
| 1.4 Сочетания…………………………………………………………………... | |
| 1.5 Сочетания с повторениями………………………………………………... | |
| 1.6 Перестановки………………………………………………………………. | |
| 1.7 Перестановки с повторениями………………………………………….… | |
| Задачи к теме 1…………………………………………………………………. | |
| 2. Элементы теории вероятностей…………………………………………. | |
| 2.1. Классификация событий. Классическое определение вероятности. Свойства вероятности…………………………………………………………. | |
| 2.2. Правила сложения и умножения вероятностей. Зависимые и независимые события…………………………………………………….……. | |
| Задачи к теме 2…………………………………………………………………. | |
| 3. Формулы полной вероятности и Байеса………………………………… | |
| Задачи к теме 3…………………………………………………………………. | |
| 4. Дискретные случайные величины………………………………………. | |
| 4.1. Определение дискретной случайной величины…………………………. | |
| 4.2. Числовые характеристики………………………………..………………. | |
| 4.3. Математические операции над случайными величинами……………… | |
| 4.4. Распределение Бернулли и Пуассона………………………………….…. | |
| 4.5. Гипергеометрическое распределение……………………………………. | |
| Задачи к теме 4……………………………………………………………….… | |
| 5. Непрерывные случайные величины………………………………….… | |
| 5.1. Функции распределения и плотность распределения непрерывной случайной величины…………………………………………………………… | |
| 5.2. Нормальное распределение……………………………………………….. | |
| Задачи к теме 5…………………………………………………………………. | |
| 6. Вариационные ряды и их характеристики……………………………... | |
| 6.1. Понятие вариационного ряда. Виды вариационных рядов………….…. | |
| 6.2. Числовые характеристики вариационного ряда…………………………. | |
| Задачи к теме 6…………………………………………………………………. | |
| 7. Выборочный метод и статистическое оценивание…………………….. | |
| 7.1. Основные понятия и определения выборочного метода………………... | |
| 7.2. Статистическое оценивание………………………………………………. | |
| 7.3. Ошибки выборки…………………………………………………………... | |
| 7.4. Определение численности (объема) выборки…………………………… | |
| 7.5. Интервальное оценивание………………………………………………… | |
| Задачи к теме 7…………………………………………………………………. | |
| 8. Проверка статистических гипотез……………………………………….. | |
| Задачи к теме 8…………………………………………………………………. | |
| Литература……………………………………………………………………... | |
| Приложения……………………………………………………………………. | |
Приложение 1. Таблица значений функции  ………….
Приложение 2. Таблица значений функции ………….
Приложение 2. Таблица значений функции 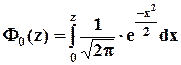 (функция Лапласа)…………………………………..
Приложение 3. Таблица значений функции Пуассона: (функция Лапласа)…………………………………..
Приложение 3. Таблица значений функции Пуассона:  ……………………………………...………..
Приложение 4. Критические точки распределения c2……………………
Приложение 5. Критические точки распределения Стьюдента………...
Приложение 6. Критические точки распределения Фишера-Снедекора………………………………………………………………….…… ……………………………………...………..
Приложение 4. Критические точки распределения c2……………………
Приложение 5. Критические точки распределения Стьюдента………...
Приложение 6. Критические точки распределения Фишера-Снедекора………………………………………………………………….……
| |
| Параметрические критерии значимости | |
Учебное издание
Практикум
|
из
5.00
|
Обсуждение в статье: Окончание приложения 6 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |
Популярное:
Как выбрать специалиста по управлению гостиницей: Понятно, что управление гостиницей невозможно без специальных знаний. Соответственно, важна квалификация...
Почему люди поддаются рекламе?: Только не надо искать ответы в качестве или количестве рекламы...

©2015-2024 megaobuchalka.ru Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. (654)
Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

