 |
Главная |
Статистическое оценивание
 2015-11-27 |
 704 |
 Обсуждений (0) |
из
5.00
|
Пусть из генеральной совокупности извлекается выборка объема n, причем значение признака х1 наблюдается m1 раз, х2 m2 раз,..., хk наблюдается mk раз, 
- объем выборки.
Мы можем сопоставить каждому значению xi относительную частоту mi/n.
Статистическим распределением выборки называют перечень возможных значений признака xi и соответствующих ему частот или относительных частот (частостей) mi (wi).
Числовые характеристики генеральной совокупности, как правило неизвестные, (средняя, дисперсия и др.) называют параметрами генеральной совокупности(обозначают, например, 
или 
, 
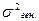). Доля единиц, обладающих тем или иным признаком в генеральной совокупности, называется генеральной долей и обозначается р.
По данным выборки рассчитывают числовые характеристики, которые называютстатистиками(обозначают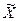 
, или 
, 
, выборочная доля обозначается w). Статистики, получаемые по различным выборкам, как правило, отличаются друг от друга. Поэтому статистика, полученная из выборки, является только оценкой неизвестного параметра генеральной совокупности. Оценка параметра - определенная числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, ее называют точечной оценкой.
В качестве точечных оценок параметров генеральной совокупности используются соответствующие выборочные характеристики. Теоретическое обоснование возможности использования этих выборочных оценок для суждений о характеристиках и свойствах генеральной совокупности дают закон больших чисел и центральная предельная теорема Ляпунова.
Выборочная средняя является точечной оценкой генеральной средней, т.е. 
≈ 
Генеральная дисперсия имеет 2 точечные оценки: -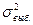 
выборочная дисперсия; 
- исправленная выборочная дисперсия[3]. - 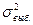исчисляется при 
, а - при 
. Причем в математической статистике доказывается, что
или 
(7.1)
При больших объемах выборк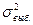и и практически совпадают.
Генеральное среднее квадратическое отклонение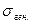 
так же имеет 2 точечные оценки: 
- выборочное среднее квадратическое отклонение и 
- исправленное выборочное среднее квадратическое отклонение. используется для оценивания 
при 
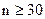, а 
для оценивания , при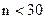 
;при этом 
, а 
.
Ошибки выборки
Поскольку выборочная совокупность представляет собой лишь часть генеральной совокупности, то вполне естественно, что выборочные характеристики не будут точно совпадать с соответствующими генеральными. Ошибка репрезентативности может быть представлена как разность между генеральными и выборочными характеристиками изучаемой совокупности: 
, либо 
.
Применительно к выборочному методу из теоремы Чебышева следует, что с вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности разность между выборочной средней и генеральной средней будет сколь угодно мала.
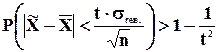(7.2)
где 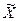- средняя по совокупности выбранных единиц,
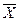- средняя по генеральной совокупности,
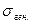- среднее квадратическое отклонение в генеральной совокупности.
Запись показывает, что о величине расхождения между параметром и статистикой 
, можно судить лишь с определенной вероятностью, от которой зависит величина t.
Формула (7.2) устанавливает связь между пределом ошибки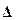 
, гарантируемым с некоторой вероятностью Р, величиной tи средней ошибкой выборки 
.
Cогласно центральной предельной теореме Ляпунова выборочные распределения статистик (при n ³ 30) будут иметь нормальное распределение независимо от того, какое распределение имеет генеральная совокупность. Следовательно:
(7.3)
где Ф0(t) - функция Лапласа.
Значения вероятностей, соответствующие различным t, содержатся в специальных таблицах: при n ³ 30 - в таблице значений Ф0(t), а при n < 30 в таблице распределения t-Стьюдента. Неизвестное значение 
при расчете ошибки выборки заменяется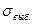 
В зависимости от способа отбора средняя ошибка выборки определяется по разному:
Таблица 7.1
| 2015-11-27 |
704 |
Обсуждений (0) |
из
5.00
|
Обсуждение в статье: Статистическое оценивание |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |
Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы