 |
Главная |
ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
 2015-11-27 |
 1464 |
 Обсуждений (0) |
из
5.00
|
На разных стадиях статистического исследования и моделирования возникает необходимость в формулировке и экспериментальной проверке некоторых предположений (гипотез) относительно природы и величины неизвестных параметров анализируемой генеральной совокупности (совокупностей). Например, исследователь высказывает предположение: "выборка извлечена из нормальной генеральной совокупности" или "генеральная средняя анализируемой совокупности равна пяти". Такие предположения называются статистическими гипотезами.
Сопоставление высказанной гипотезы относительно генеральной совокупности с имеющимися выборочными данными, сопровождаемое количественной оценкой степени достоверности получаемого вывода, осуществляется с помощью того или иного статистического критерия и называется проверкой статистических гипотез.
Выдвинутая гипотеза называется нулевой (основной). Ее принято обозначать Н0.
По отношению к высказанной (основной) гипотезе всегда можно сформулировать альтернативную (конкурирующую), противоречащую ей. Альтернативную (конкурирующую) гипотезу принято обозначать Н1.
Цель статистической проверки гипотез состоит в том, чтобы на основании выборочных данных принять решение о справедливости основной гипотезы Н0.
Если выдвигаемая гипотеза сводится к утверждению о том, что значение некоторого неизвестного параметра генеральной совокупности в точности равно заданной величине, то эта гипотеза называется простой, например: "среднедушевой совокупный доход населения России составляет 650 рублей в месяц"; "уровень безработицы (доля безработных в численности экономически активного населения) в России равна 9%" . В других случаях гипотеза называется сложной.
В качестве нулевой гипотезы Н0 принято выдвигать простую гипотезу, т.к. обычно бывает удобнее проверять более строгое утверждение.
По своему содержанию статистические гипотезы можно подразделить на несколько основных типов[6]:
- гипотезы о виде закона распределения исследуемой случайной величины;
- гипотезы о числовых значениях параметров исследуемой генеральной совокупности[7];
- гипотезы об однородности двух или нескольких выборок или некоторых характеристик анализируемых совокупностей;
- гипотезы об общем виде модели, описывающей статистическую зависимость между признаками и др.
Так как проверка статистических гипотез осуществляется на основании выборочных данных, т.е. ограниченного ряда наблюдений, решения относительно нулевой гипотезы Н0 имеют вероятностный характер. Другими словами, такое решение неизбежно сопровождается некоторой, хотя возможно и очень малой, вероятностью ошибочного заключения как в ту, так и в другую сторону.
Так, в какой-то небольшой доле случаев α нулевая гипотеза Н0 может оказаться отвергнутой, в то время как в действительности в генеральной совокупности она является справедливой. Такую ошибку называют ошибкой первого рода. А ее вероятность принято называтьуровнем значимости и обозначать α.
Наоборот, в какой-то небольшой доле случаев β нулевая гипотеза Н0 принимается, в то время как на самом деле в генеральной совокупности она ошибочна, а справедлива альтернативная гипотеза Н1. Такую ошибку называют ошибкой второго рода. Вероятность ошибки второго рода принято обозначать β. Вероятность 1 - β называют мощностью критерия.
При фиксированном объеме выборки можно выбрать по своему усмотрению величину вероятности только одной из ошибок α или β. Увеличение вероятности одной из них приводит к снижению другой. Принято задавать вероятность ошибки первого рода α - уровень значимости. Как правило, пользуются некоторыми стандартными значениями уровня значимости α: 0,1; 0,05; 0,025; 0,01; 0,005; 0,001. Тогда, очевидно, из двух критериев, характеризующихся одной и той же вероятностью α отклонить правильную в действительности гипотезу Н0, следует принять тот, который сопровождается меньшей ошибкой второго рода β, т.е. большей мощностью. Снижения вероятностей обеих ошибок α и β можно добиться путем увеличения объема выборки.
Правильное решение относительно нулевой гипотезы Н0 также может быть двух видов:
- будет принята нулевая гипотеза Н0, тогда как и на самом деле в генеральной совокупности верна нулевая гипотеза Н0 ; вероятность такого решения 1 - α;
- нулевая гипотеза Н0 будет отклонена в пользу альтернативной Н1, тогда как и на самом деле в генеральной совокупности нулевая гипотеза Н0 отклоняется в пользу альтернативной Н1; вероятность такого решения 1 - β - мощность критерия.
Результаты решения относительно нулевой гипотезы можно проиллюстрировать с помощью таблицы 8.1.
Таблица 8.1
| Нулевая гипотеза Н0 | Результаты решения относительно нулевой гипотезы Н0 | |
| отклонена | принята | |
| верна | ошибка первого рода, ее вероятность Р(Н1/Н0) = α | правильное решение, его вероятность Р(Н0/Н0) = 1 - α |
| не верна | правильное решение, его вероятность Р(Н1/Н1) = 1 - β | ошибка второго рода, ее вероятность Р(Н0/Н1) = β |
Проверка статистических гипотез осуществляется с помощью статистического критерия (назовем его в общем виде К), являющего функцией от результатов наблюдения.
Статистический критерий - это правило (формула), по которому определяется мера расхождения результатов выборочного наблюдения с высказанной гипотезой Н0.
Статистический критерий, как и всякая функция от результатов наблюдения, является случайной величиной и в предположении справедливости нулевой гипотезы Н0подчинена некоторому хорошо изученному (и затабулированному) теоретическому закону распределения с плотностью распределения f(k).
Выбор критерия для проверки статистических гипотез может быть осуществлен на основании различных принципов. Чаще всего для этого пользуются принципом отношения правдоподобия, который позволяет построить критерий наиболее мощный среди всех возможных критериев. Суть его сводится к выбору такого критерия К с известной функцией плотности f(k) при условии справедливости гипотезы Н0, чтобы при заданном уровнем значимости α можно было бы найти критическую точку Ккр.распределения f(k), которая разделила бы область значений критерия на две части: область допустимых значений, в которой результаты выборочного наблюдения выглядят наиболее правдоподобными, и критическую область, в которой результаты выборочного наблюдения выглядят менее правдоподобными в отношении нулевой гипотезы Н0.
Если такой критерий К выбран, и известна плотность его распределения, то задача проверки статистической гипотезы сводится к тому, чтобы при заданном уровне значимости α рассчитать по выборочным данным наблюдаемое значение критерия Кнабл. и определить является ли оно наиболее или менее правдоподобным в отношении нулевой гипотезы Н0.
Проверка каждого типа статистических гипотез осуществляется с помощью соответствующего критерия, являющегося наиболее мощным в каждом конкретном случае. Например, проверка гипотезы о виде закона распределения случайной величины может быть осуществлена с помощью критерия согласия Пирсона χ2; проверка гипотезы о равенстве неизвестных значений дисперсий двух генеральных совокупностей - с помощью критерия F - Фишера; ряд гипотез о неизвестных значениях параметров генеральных совокупностей проверяется с помощью критерия Z - нормальной распределенной случайной величины и критерия T- Стьюдента и т.д.
Значение критерия, рассчитываемое по специальным правилам на основании выборочных данных, называется наблюдаемым значением критерия (Кнабл.).
Значения критерия, разделяющие совокупность значений критерия на область допустимых значений (наиболее правдоподобных в отношении нулевой гипотезы Н0) и критическую область (область значений, менее правдоподобных в отношении таблицам распределения случайной величины К, выбранной в качестве критерия, называются критическими точками(Ккр.).
Областью допустимых значений (областью принятия нулевой гипотезы Н0) называют совокупность значений критерия К, при которых нулевая гипотеза Н0 не отклоняется.
Критической областью называют совокупность значений критерия К, при которых нулевая гипотеза Н0 отклоняется в пользу конкурирующей Н1.
Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.
Если конкурирующая гипотеза - правосторонняя, например, Н1: а > а0, то и критическая область - правосторонняя (рис 1). При правосторонней конкурирующей гипотезе критическая точка (Ккр. правосторонняя)принимает положительные значения.
Если конкурирующая гипотеза - левосторонняя, например, Н1: а < а0, то и критическая область - левосторонняя (рис 2). При левосторонней конкурирующей гипотезе критическая точка принимает отрицательные значения (Ккр. левосторонняя).
Если конкурирующая гипотеза - двусторонняя, например, Н1: а ¹ а0, то и критическая область - двусторонняя (рис 3). При двусторонней конкурирующей гипотезе определяются две критические точки (Ккр. левосторонняя и Ккр. правосторонняя).
 |
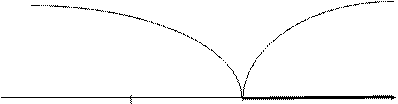Область допустимых Критическая
значений область
К
0 Ккр.
Рис 8.1. Правосторонняя критическая область.
 |
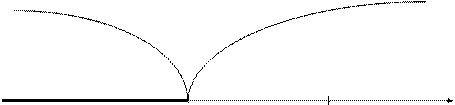Критическая Область допустимых
область значений
К
-Ккр. 0
Рис 8.2. Левосторонняя критическая область.
 |
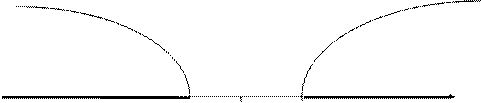Критическая Область допустимых Критическая
область значений область
К
-Ккр. 0 Ккр.
Рис 8.3. Двусторонняя критическая область.
Основной принцип проверки статистических гипотез состоит в следующем:
- если наблюдаемое значение критерия (Кнабл.) принадлежит критической области, то нулевая гипотеза Н0 отклоняется в пользу конкурирующей Н1;
- если наблюдаемое значение критерия (Кнабл.) принадлежит области допустимых значений, то нулевую гипотезу Н0 нельзя отклонить.
Можно принять решение относительно нулевой гипотезы Н0 путем сравнения наблюдаемого (Кнабл.) и критического значений критерия (Ккр.).
При правосторонней конкурирующей гипотезе:
Если Кнабл. £ Ккр., то нулевую гипотезу Н0 нельзя отклонить;
если Кнабл. > Ккр., то нулевая гипотеза Н0 отклоняется в пользу конкурирующей Н1.
При левосторонней конкурирующей гипотезе:
Если Кнабл. ³ - Ккр., то нулевую гипотезу Н0 нельзя отклонить;
если Кнабл. < - Ккр., то нулевая гипотеза Н0 отклоняется в пользу конкурирующей Н1.
При двусторонней конкурирующей гипотезе:
Если - Ккр. £ Кнабл. £ Ккр., то нулевую гипотезу Н0 нельзя отклонить;
если Кнабл. > Ккр. или Кнабл. < - Ккр., то нулевая гипотеза Н0 отклоняется в пользу конкурирующей Н1.
Алгоритм проверки статистических гипотез сводится к следующему:
1. Сформулировать нулевую Н0 и альтернативную Н1 гипотезы;
2. Выбрать уровень значимости a;
3. В соответствии с видом выдвигаемой нулевой гипотезы Н0 выбрать статистический критерий для ее проверки, т.е. - специально подобранную случайную величину К, точное или приближенное распределение которой заранее известно;
4. По таблицам распределения случайной величины К, выбранной в качестве статистического критерия, найти его критическое значение Ккр. (критическую точку или точки);
5. На основании выборочных данных по специальному алгоритму вычислитьнаблюдаемое значение критерия Кнабл.;
6. По виду конкурирующей гипотезы Н1 определить тип критической области;
7. Определить, в какую область (допустимых значений или критическую) попадает наблюдаемое значение критерия Кнабл., и в зависимости от этого - принять решение относительно нулевой гипотезы Н0.
Следует заметить, что даже в том случае, если нулевую гипотезу Н0 нельзя отклонить, это не означает, что высказанное предположение о генеральной совокупности является единственно подходящим: просто ему не противоречат имеющиеся выборочные данные, однако таким же свойством наряду с высказанной могут обладать и другие гипотезы.
Можно интерпретировать результаты проверки нулевой гипотезы следующим образом:
- если в результате проверки нулевую гипотезу Н0 нельзя отклонить, то это означает, что имеющиеся выборочные данные не позволяют с достаточной уверенностью отклонить нулевую гипотезу Н0, вероятность нулевой гипотезы Н0 больше α, а конкурирующей Н1 - меньше 1 - α;
- если в результате проверки нулевая гипотеза Н0 отклоняется в пользу конкурирующей Н1, то это означает, что имеющиеся выборочные данные не позволяют с достаточной уверенностью принять нулевую гипотезу Н0, вероятность нулевой гипотезы Н0 меньше α, а конкурирующей Н1 - больше 1 - α.
Пример 8.1В семи случаях из десяти фирма-конкурент компании "А" действовала на рынке так, как будто ей заранее были известны решения, принимаемые фирмой "А". На уровне значимости 0,05 определите, случайно ли это, или в фирме "А" работает осведомитель фирмы-конкурента?
Решение.Для того чтобы ответить на вопрос данной задачи, необходимо проверить статистическую гипотезу о том, совпадает ли данное эмпирическое распределение числа действий фирмы-конкурента с равномерным теоретическим распределением?
Если ходы, предпринимаемые конкурентом, выбираются случайно, т.е. в фирме "А" - нет осведомителя (инсайдера), то число "правильных" и "неправильных" ее действий должно распределиться поровну, т.е. по 5 (10/2). А это и есть отличительная особенность равномерного распределения.
Этот вид статистических гипотез относится к гипотезам о виде закона распределения генеральной совокупности. 
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: Х~R(a; b) - случайная величина Х подчиняется равномерному распределению с параметрами (a; b) (в контексте задачи - "в фирме "А" - нет осведомителя (инсайдера)"; "распределение числа удачных ходов фирмы-конкурента - случайно").
Н1: Случайная величина Х не подчиняется равномерному распределению (в контексте задачи - "в фирме "А" - есть осведомитель (инсайдер)"; "распределение числа удачных ходов фирмы-конкурента - не случайно").
В качестве критерия для проверки статистических гипотез о неизвестном законе распределения генеральной совокупности используется случайная величина c2 . Этот критерий называют критерием Пирсона.
Его наблюдаемое значение (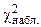 
) рассчитывается по формуле:
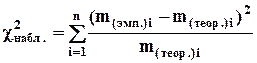, (8.1)
где m(эмп.)i - эмпирическая частота i-той группы выборки;
m(теор.)i - теоретическая частота i-той группы выборки.
Составим таблицу распределения эмпирических и теоретических частот:
| m(эмп.)i | ||
| m(теор.)i |
Найдем наблюдаемое значение :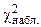
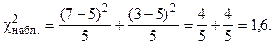
Критическое значение (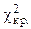 
) следует определять по таблице распределения c2 (см. приложение 4) по уровню значимости a и числу степеней свободы k.
По условию a = 0,05, а число степеней свободы рассчитывается по формуле:
k = n - l -1,
где k - число степеней свободы;
n - число групп выборки;
l - число неизвестных параметров предполагаемой модели, оцениваемых по данным выборки (если все параметры предполагаемого закона известны точно, то l = 0).
По условию задачи число групп выборки (n) равно 2, т.к. могут быть только два варианта действий фирмы-конкурента: "удачные" и "неудачные", а число неизвестных параметров равномерного распределения (l) равно 0.
Отсюда, k = 2 - 0 - 1 = 1.
Найдем 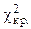по уровню значимости a = 0,05 и числу степеней свободы k=1.
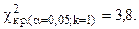
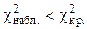, следовательно, на данном уровне значимости нулевую гипотезу нельзя отклонить, расхождения эмпирических и теоретических частот - незначимые. Данные наблюдений согласуются с гипотезой о равномерном распределении генеральной совокупности.
Это означает, что для утверждения о том, что действия фирмы-конкурента на рынке неслучайны; на уровне значимости a = 0,05 можно утверждать, что в фирме "А" нет платного осведомителя фирмы-конкурента.
Ответ. на уровне значимости a = 0,05 можно утверждать, что в фирме "А" нет платного осведомителя фирмы-конкурента.
Пример 8.2На уровне значимости a = 0,025 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
| m(эмп.)i | ||||||
| m(теор.)i |
Решение.Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: Х~N(a; s2) - случайная величина Х подчиняется нормальному закону распределения с параметрами а и s2.
Н1: Случайная величина Х не подчиняется нормальному закону распределения с параметрами а и s2.
В качестве критерия для проверки нулевой гипотезы используем критерий Пирсона c2 .
Найдем наблюдаемое значение ( ):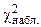
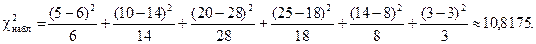
Найдем критическое значение критерия ( 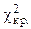) по таблице распределения c2 (приложение 4) по уровню значимости a и числу степеней свободы k.
По условию a = 0,025; число степеней свободы найдем по формуле:
k = n - l -1,
где k - число степеней свободы;
n - число групп выборки;
l - число неизвестных параметров предполагаемой модели, оцениваемых по данным выборки.
По условию задачи число групп выборки (n) равно 6, а число неизвестных параметров нормального распределения (l) равно 2.
Отсюда, k = 6 - 2 - 1 = 3.
Найдем 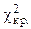по уровню значимости a = 0,025 и числу степеней свободы k=3.
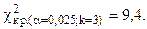
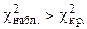, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей, расхождения эмпирических и теоретических частот - значимые. Данные наблюдений не согласуются с гипотезой о нормальном распределении генеральной совокупности.
Ответ. На уровне значимости a = 0,025 данные наблюдений не согласуются с гипотезой о нормальном распределении генеральной совокупности.
Пример 8.3 Техническая норма предусматривает в среднем 40 сек. на выполнение определенной технологической операции на конвейере по производству часов. От работниц, работающих на этой операции, поступили жалобы, что они в действительности затрачивают на эту операцию больше времени. Для проверки данной жалобы произведены хронометрические измерения времени выполнения этой технологической операции у 16 работниц, занятых на этой операции, и получено среднее время выполнения операции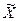 
= 42 сек. Можно ли по имеющимся хронометрическим данным на уровне значимости a = 0,01 отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, если:
а) исправленное выборочное среднее квадратическое отклонение s составило 3,5 сек.;
б) выборочное среднее квадратическое отклонение 
составило 3,5 сек.?
Решение. а) Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна определенному числу, когда дисперсия генеральной совокупности неизвестна (выборка мала, т.к. n = 16, меньше 30).
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: a = а0 = 40 - неизвестное математическое ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) равно гипотетическому предполагаемому числовому значению а0 (применительно к условию данной задачи - время выполнения технологической операции соответствует норме).
Н1: a > 40 - неизвестное математическое ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) больше числовому значению а0 (применительно к условию данной задачи - время выполнения технологической операции больше установленной нормы).
Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.
В качестве критерия для сравнения неизвестного математического ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) с гипотетическим числовым значением а0, используется случайная величина t - критерий Стьюдента:
Его наблюдаемое значение (tнабл.) рассчитывается по формуле:
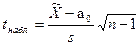. (8.2)
где 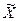- выборочная средняя;
а0 - числовое значение генеральной средней;
s - исправленное среднее квадратическое отклонение;
n - объем выборки.
Найдем наблюдаемое значение tнабл.:
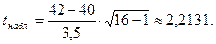
Критическое значение (tкр.) следует находить по таблице распределения Стьюдента (приложение 5) по уровню значимости a и числу степеней свободы k.
По условию a = 0,01; число степеней свободы найдем по формуле:
k = n - 1,
где k - число степеней свободы;
n - объем выборки.
k = 16 - 1 = 15.
Найдем tкр. по уровню значимости a = 0,01 (для односторонней критической области) и числу степеней свободы k = 15:
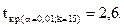
Заметим, что при левосторонней конкурирующей гипотезе Н1: a < 40 tкр. следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для односторонней критической области) и числу степеней свободы k = n - 1 и присваивать ему "минус";
При двусторонней конкурирующей гипотезе Н1: a ¹ 40 tкр. следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для двусторонней критической области) и числу степеней свободы k = n - 1).
tнабл. < tкр, следовательно, на данном уровне значимости нет оснований отклонить нулевую гипотезу.
Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 нельзя отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме. Следовательно, жалобы работниц - необоснованны.
 |
Область допустимых Критическая
значений область
t
0 tнабл.= 2,21 tкр.= 2,6
Рис 8.4.
Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нет оснований отклонить нулевую гипотезу.
б) Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна определенному числу, когда дисперсия генеральной совокупности неизвестна.
Алгоритм решения задачи будет тот же, что и в первом случае. Однако наблюдаемое значение tнабл. будет рассчитывается по формуле:
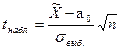. (8.3)
где 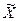- выборочная средняя;
а0 - числовое значение генеральной средней;
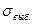- выборочное среднее квадратическое отклонение;
n - объем выборки.
Найдем наблюдаемое значение (tнабл.):
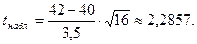
Критическое значение (tкр.) следует находить по таблице распределения Стьюдента (приложение 5) по уровню значимости a и числу степеней свободы k.
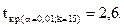
tнабл. < tкр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу, жалобы работниц - необоснованны.
Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 нельзя отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, жалобы работниц - необоснованны.
Пример 8.4 Изменим условие предидущей задачи. Техническая норма предусматривает в среднем 40 сек. на выполнение определенной технологической операции на конвейере по производству часов. От работниц, работающих на этой операции, поступили жалобы, что они в действительности затрачивают на эту операцию больше времени. Для проверки данной жалобы произведены хронометрические измерения времени выполнения этой технологической операции у 36 работниц, занятых на этой операции, и получено среднее время выполнения операции 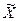= 42 сек. Можно ли (предполагая время выполнения технологической операции случайной величиной, подчиняющейся нормальному закону) по имеющимся хронометрическим данным на уровне значимости a = 0,01 отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, если известно, что среднее квадратическое отклонение генеральной совокупности s составляет 3,5 сек.?
Решение.Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна числовому значению, когда дисперсия генеральной совокупности известна (большая выборка, т.к. n = 36, больше 30).
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: a = а0 = 40 - неизвестная генеральная средняя нормально распределенной совокупности с известной дисперсией равна числовому значению (применительно к условию данной задачи - время выполнения технологической операции соответствует норме).
Н1: a > 40 - неизвестная генеральная средняя нормально распределенной совокупности с известной дисперсией больше числового значения (применительно к условию данной задачи - время выполнения технологической операции больше установленной нормы).
Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.
В качестве критерия для сравнения выборочной средней с гипотетической генеральной средней нормальной совокупности, когда дисперсия генеральной совокупности известна, используется случайная величина U:
Его наблюдаемое значение (uнабл.) рассчитывается по формуле:
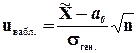. (8.4)
где 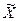- выборочная средняя;
а0 - числовое значение генеральной средней;
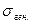- выборочное среднее квадратическое отклонение;
n - объем выборки.
Найдем наблюдаемое значение (uнабл.):
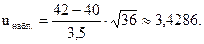
Так как конкурирующая гипотеза - правосторонняя, критическое значение uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства:
Ф0(uкр ) = (1 - 2a) / 2.
По условию a = 0,01.
Отсюда:
Ф0(uкр ) = (1 - 2·0,01) / 2 = 0,49.
По таблице функции Лапласа (приложение 2) найдем при каком uкр. Ф0(uкр ) = 0,49.
F0(2,33) = 0,49.
Следовательно: uкр. = 2,33.
Заметим, что при левосторонней конкурирующей гипотезе Н1: a < 40 uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(uкр) = (1 - 2a) / 2 и присваивать ему "минус".
При двусторонней конкурирующей гипотезе Н1: a ¹ 40 uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(uкр ) = (1 - a) / 2).
uнабл. > uкр, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей. По имеющимся хронометрическим данным с более чем 99%-ной надежностью можно утверждать, что среднее время выполнения этой операции превышает норму. Следовательно, жалобы работниц - обоснованны.
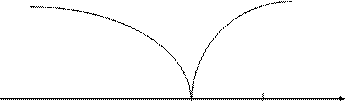
Область допустимых Критическая
значений область
U
0 uкр.= 2,33 uнабл.= 3,43
Рис. 8.5.
Наблюдаемое значение критерия попадает в критическую область, следовательно, нулевая гипотеза отвергается в пользу конкурирующей.
Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 можно утверждать, что среднее время выполнения этой операции превышает норму, жалобы работниц - обоснованны.
Пример 8.5 Экономический анализ производительности труда предприятий отрасли позволил выдвинуть гипотезу о наличии двух типов предприятий с различной средней величиной показателя производительности труда. Выборочное обследование 42-х предприятий первой группы дало следующие результаты: средняя производительность труда 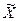составила 119 деталей. По данным выборочного обследования 35-и предприятий второй группы средняя производительность труда 
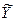составила 107 деталей. Генеральные дисперсии известны: D(X) = 126,91 (дет.2); D(Y) = 136,1 (дет.2). Считая, что выборки извлечены из нормально распределенных генеральных совокупностей Х и Y, на уровне значимости 0,05 проверьте, случайно ли полученное различие средних показателей производительности труда в группах или же имеются два типа предприятий с различной средней величиной производительности труда.
Решение.Для решения данной задачи необходимо сравнить две средние нормально распределенных генеральных совокупностей, генеральные дисперсии которых известны (большие независимые выборки). В данной задаче речь идет о больших выборках, так как nx = 42 и ny = 35 больше 30. Выборки - независимые, так как из контекста задачи видно, что они извлечены из непересекающихся генеральных совокупностей.
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: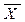 
= 
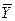- генеральные средние двух нормально распределенных совокупностей с известными дисперсиями равны (применительно к условию данной задачи - предприятия двух групп относятся к одному типу предприятий, - средняя производительность труда в двух группах - одинакова).
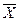Н1: 
¹ 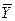- генеральные средние двух нормально распределенных совокупностей с известными дисперсиями не равны (применительно к условию данной задачи - предприятия двух групп относятся к разному типу предприятий, - средняя производительность труда в двух группах - неодинакова).
Выдвигаем двустороннюю конкурирующую гипотезу, так как из условия задачи не следует, что необходимо выяснить больше или меньше производительность труда в одной из групп предприятий по сравнению с другой.
Так как конкурирующая гипотеза - двусторонняя, то и критическая область - двусторонняя.
В качестве критерия для сравнения двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки), используется случайная величина Z.
Его наблюдаемое значение (zнабл.) рассчитывается по формуле:
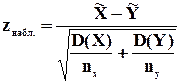, (8.5)
где 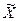- выборочная средняя для X;
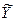- выборочная средняя для Y;
D(X) - генеральная дисперсия для X;
D(Y) - генеральная дисперсия для Y;
nx - объем выборки для X;
ny - объем выборки для Y.
Найдем наблюдаемое значение (zнабл.):
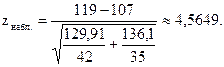
Так как конкурирующая гипотеза - двусторонняя, критическое значение (zкр.) следует находить по таблице функции Лапласа (приложение 2) из равенства:
Ф0(zкр ) = (1 - a) / 2.
По условию a = 0,05.
Отсюда:
Ф0(zкр ) = (1 - 0,05) / 2 = 0,475.
По таблице функции Лапласа (приложение 2) найдем при каком zкр. Ф0(zкр ) = 0,475.
F0(1,96) = 0,475.
Учитывая, что конкурирующая гипотеза - двусторонняя, находим две критические точки:
zкр.(прав.) = 1,96; zкр.(лев.) = - 1,96.
Заметим, что при левосторонней конкурирующей гипотезе Н1: 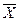< 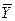zкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(zкр ) = (1 - 2a) / 2 и присваивать ему "минус".
При правосторонней конкурирующей гипотезе Н1: 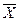> 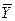zкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(zкр ) = (1 - 2a) / 2).
zнабл. > zкр, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей. На уровне значимости a = 0,05 можно утверждать, что полученное различие средних показателей производительности труда в группах - неслучайно, имеются два типа предприятий с различной средней величиной производительности труда.
 |
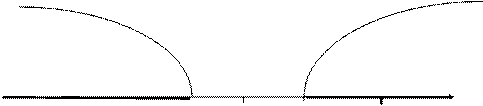Критическая Область допустимых Критическая
область значений область
Z
-zкр. = -1,96 0 zкр.= 1
| 2015-11-27 |
1464 |
Обсуждений (0) |
из
5.00
|
Обсуждение в статье: ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |
Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы