 |
Главная |
Сфера, вписанная в многогранник или тело вращения
|
из
5.00
|
Сфера называется вписанной в многогранник, если она касается всех граней многогранника.
Многогранник соответственно называется описанным около сферы.
Теоремы.
1. Сферу можно вписать в призму, если призма прямая и ее высота равна диаметру окружности, вписанной в основание призмы.
2. Сферу можно вписать в пирамиду, если в основание можно вписать окружность, а вершина пирамиды ортогонально проектируется в центр этой окружности.
3. Сферу можно вписать в любую правильную пирамиду.
Сфера называется вписанной в цилиндр, если она касается оснований и боковой поверхности цилиндра. Цилиндр соответственно называется описанным около сферы.
Теорема. Для того чтобы сферу можно было вписать в цилиндр, необходимо и достаточно, чтобы высота цилиндра равнялась диаметру его основания.
Сфера называется вписанной в конус, если она касается основания и боковой поверхности конуса. Конус соответственно называется описанным около сферы.
Теорема. Сферу можно вписать в любой конус.
Сфера называется вписанной в усеченный конус, если она касается оснований и боковой поверхности конуса. Усеченный конус соответственно называется описанным около сферы.
Теорема. Для того чтобы сферу можно было вписать в усеченный конус, необходимо и достаточно, чтобы образующая усеченного конуса равнялась сумме радиусов оснований.
Теорема.
Сферу можно вписать в тело вращения, если в осевое сечение можно вписать окружность.
Сфера, описанная около многогранника или тела вращения
Сфера называется описанной около многогранника, если все вершины многогранника лежат на сфере. Многогранник соответственно называется вписанным в сферу.
Теоремы.
1. Для того чтобы сферу можно было описать около призмы, необходимо и достаточно, чтобы призма была прямая и около основания можно было описать окружность.
2. Для того чтобы сферу можно было описать около пирамиды, необходимо и достаточно, чтобы около основания можно было описать окружность.
3. Сферу можно описать около любой правильной пирамиды.
Сфера называется описанной около цилиндра, если окружности оснований цилиндра лежат на сфере. Цилиндр соответственно называется вписанным в сферу.
Теорема. Сферу можно описать около любого цилиндра.
Сфера называется описанной около конуса, если окружность основания и вершина конуса лежат на сфере. Конус соответственно называется вписанным в сферу.
Теорема. Сферу можно описать около любого конуса.
Сфера называется описанной около усеченного конуса, если окружности оснований конуса лежат на сфере. Усеченный конус соответственно называется вписанным в сферу.
Теорема. Сферу можно описать около любого усеченного конуса.
Многогранники и тела вращения
Цилиндр называется описанным около призмы, если окружности оснований цилиндра описаны около оснований призмы, а боковые ребра призмы являются образующими цилиндра. Призма соответственно называется вписанной в цилиндр.
Теорема. Для того чтобы около призмы можно было описать цилиндр, необходимо и достаточно, чтобы призма была прямая и около ее основания можно было описать окружность.
Цилиндр называется вписанным в призму, если окружности его оснований вписаны в основания призмы, а боковая поверхность касается боковых граней призмы.
Теорема. Для того чтобы в призму можно было вписать цилиндр, необходимо и достаточно, чтобы призма была прямая и в ее основание можно было вписать окружность.
Конус называется описанным около пирамиды, если окружность основания конуса описана около основания пирамиды, а боковые ребра пирамиды являются образующими конуса. Пирамида соответственно называется вписанной в конус.
Теорема. Для того чтобы около пирамиды можно было описать конус, необходимо и достаточно, чтобы боковые ребра пирамиды были равны.
Конус называется вписанным в пирамиду, если окружность его основания вписана в основание пирамиды, а боковая поверхность касается боковых граней пирамиды. Пирамида соответственно называется описанной около конуса.
Теорема. Для того чтобы в пирамиду можно было вписать конус, необходимо и достаточно, чтобы в основание пирамиды можно было вписать окружность, а вершина пирамиды ортогонально проектировалась в центр этой окружности.
Задания для самостоятельного решения
I уровень
1.1. В правильную четырехугольную пирамиду с объемом  вписан конус. Найдите его объем.
вписан конус. Найдите его объем.
1.2. В конус, образующая которого наклонена к плоскости основания под углом a, вписана пирамида. Основание пирамиды – прямоугольный треугольник с катетами 3 см и 4 см. Найдите объем пирамиды, если 
1.3. Около цилиндра описана правильная четырехугольная призма, периметр основания которого равен 12 см, а площадь боковой поверхности равна 48 см2. Найдите площадь полной поверхности цилиндра.
1.4. В равносторонний цилиндр, диагональ осевого сечения которого равна  вписана правильная шестиугольная призма. Вычислите площадь боковой поверхности призмы.
вписана правильная шестиугольная призма. Вычислите площадь боковой поверхности призмы.
1.5. Усеченный конус описан около правильной треугольной усеченной пирамиды. Радиус верхнего основания в 2 раза меньше радиуса нижнего основания конуса, высота равна 4 см, а образующая 5 см. Найдите площадь боковой поверхности усеченной пирамиды.
1.6. В куб вписан шар и около куба описан шар. Найдите отношение объемов этих шаров.
1.7. В сферу вписан цилиндр. Площадь основания цилиндра 16p см2, тангенс угла наклона диагонали его осевого сечения к плоскости основания равен 3. Найдите площадь сферы.
1.8. В конус, площадь боковой поверхности которого в 2 раза больше площади основания, вписан шар. Найдите радиус шара, если образующая конуса равна 8 см.
1.9. В цилиндрическую мензурку, диаметр которой 2,5 см, заполненную водой до некоторого уровня, опускают четыре равных металлических шариков диаметром в 1 см. Определите, на сколько изменится уровень воды в мензурке.
1.10. Основание шарового слоя и цилиндра совпадают. Объем тела, заключенного между их боковыми поверхностями, равен 36p см3. Найдите высоту шарового слоя.
II уровень
2.1. Равносторонний треугольник, сторона которого равна а, вращается вокруг внешней оси, параллельной его высоте и удаленной от нее на  Найдите площадь поверхности полученного тела вращения.
Найдите площадь поверхности полученного тела вращения.
2.2. Усеченный конус вписан в четырехугольную усеченную пирамиду, основание которой – ромб со стороной а и углом a. Площадь боковой поверхности пирамиды равна S, боковые грани наклонены к основанию пирамиды под углом b. Найдите объем усеченного конуса.
2.3. В правильной треугольной призме боковое ребро равно стороне основания. Около призмы описан шар, а около шара описан конус. Образующая конуса равна l и составляет с плоскостью основания угол a. Найдите объем призмы.
2.4. В пирамиде, все боковые грани которой равнонаклонены к плоскости основания, через центр вписанного шара проведена плоскость, параллельная плоскости основания. Отношение площади сечения пирамиды этой плоскостью к площади основания равно k. Найдите угол между боковой гранью и основанием пирамиды.
2.5. В шар радиуса R вписаны два конуса с общим основанием. Вершины конусов совпадают с противоположными концами диаметра шара. Шаровой сегмент, вмещающий меньший конус, имеет в осевом сечении дугу a. Найдите расстояние между центрами шаров, вписанный в эти конусы.
2.6. Шар касается всех боковых ребер правильной четырехугольной призмы и ее оснований. Найдите отношение площади поверхности шара, лежащей вне призмы, к площади полной поверхности призмы.
2.7. В правильную четырехугольную пирамиду вписан равносторонний цилиндр так, что одна из его образующих расположена на диагонали основания пирамиды, а окружность основания касается двух сменных боковых граней пирамиды. Найдите радиус основания цилиндра, если боковое ребро пирамиды равно b, а угол его наклона к плоскости основания равен a.
2.8. Ребро тетраэдра равно 8 см. Цилиндрическая поверхность проходит через одно из его ребер и через все его вершины. Найдите радиус основания цилиндра.
2.9. Ребра треугольной пирамиды, выходящие из вершины S, попарно перпендикулярны и равны a, b и c. Найдите объем куба, вписанного в пирамиду так, что одна из его вершин совпадает с вершиной S пирамиды.
2.10. В усеченный конус вписан шар, объем которого составляет  объема конуса. Найдите угол наклона образующей к плоскости нижнего основания конуса.
объема конуса. Найдите угол наклона образующей к плоскости нижнего основания конуса.
Ответы к задачам
Раздел 11.1
I уровень
1.6. 30º. 1.7. 14. 1.8. 
II уровень
2.3.  2.4.
2.4.  2.5. 10 см. 2.6.
2.5. 10 см. 2.6. 
2.7. 74. 2.8. 5 см. 2.9. 1 см 2.10. 
III уровень
3.1.  3.2.
3.2.  3.3.
3.3. 
3.4.  3.5.
3.5. 
Раздел 12.2.
I уровень
1.1.  см. 1.2. 35200 м3. 1.3.
см. 1.2. 35200 м3. 1.3. 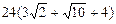 см2.
см2.
1.4.  см;
см;  см. 1.5. 288 см3. 6. 108 см3.
см. 1.5. 288 см3. 6. 108 см3.
1.7.  см2. 1.8. 495 кг.
см2. 1.8. 495 кг.
1.9.  дм2. 1.10. 125 см3.
дм2. 1.10. 125 см3.
II уровень
2.1.  см2. 2.2.
см2. 2.2.  см2. 2.3. 75 см3.
см2. 2.3. 75 см3.
2.4. 45°. 2.5. 788 см2. 2.6. 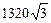 см3.
см3.
2.17. 4дм; 4 дм;  дм. 2.18.
дм. 2.18.  см3. 2.19. 30 см3.
см3. 2.19. 30 см3.
2.10. 216 мм3.
III уровень
3.1.  см2. 3.2. 72 см2. 3.3. 928 см2. 3.4. 36 см3.
см2. 3.2. 72 см2. 3.3. 928 см2. 3.4. 36 см3.
3.5. 21 см. 3.6.  3.7. 216 см2.
3.7. 216 см2.
3.8. 5:7. 3.9. 
Раздел 11.3
I уровень
1.1.  3. 1.2.
3. 1.2.  1.3.
1.3. 
1.4.  1.5.
1.5.  1.6. 3.
1.6. 3.
1.7.  5. 1.8. 728. 1.9. 2. 1.10. 798.
5. 1.8. 728. 1.9. 2. 1.10. 798.
II уровень
2.1.  13. 2.2. 4. 2.3.
13. 2.2. 4. 2.3. 
2.4.  2.5. »2,6 млн м3. 2.6.
2.5. »2,6 млн м3. 2.6. 
2.7. 770. 2.8.  2.9. 1,46 м3. 2.10.
2.9. 1,46 м3. 2.10. 
III уровень
3.1.  3.2. 60º. 3.3.
3.2. 60º. 3.3. 
3.4.  3.5.
3.5. 
3.6. 


 3.7. 48;
3.7. 48; 

3.8. 240. 3.9. 1,9. 3.10. 

Раздел 11.4
I уровень
1.1. 10. 1.2. 16p. 1.3. pS. 1.4. 60p.
1.5. 36p. 1.6.  1.8.
1.8. 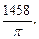
1.9. увеличится в 2,5 раза. 1.10. 1 : 3.
II уровень
2.1. 12. 2.2. 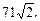 2.3.
2.3.  2.4.
2.4. 
2.5.  2.6. 0,25. 2.7.
2.6. 0,25. 2.7.  2.8. 0,17 м.
2.8. 0,17 м.
III уровень
3.1.  3.2.
3.2. 
3.3.  3.4.
3.4. 
Раздел 11.5
I уровень
1.1. 3 см. 1.2. 10 см. 1.3. 60p м2.
1.4. Увеличится в 1,5 раза. 1.5. 20 м2. 1.6. 3p см3.
1.7. 9p см2. 1.8. 224p см2. 1.9. 8,8p дм2. 1.10. 248p см
II уровень
2.1.  см. 2.2.
см. 2.2. 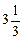 см,
см,  см. 2.3. 100p см2.
см. 2.3. 100p см2.
2.4. 375p см2 или 500p см2. 2.5. 60°.
2.6. 79%. 2.7. 5,5 см; 10,5 см. 2.8. 5418p см2.
2.9. 476p см2. 2.10. 10 дм; 16 дм.
III уровень
3.1.  . 3.2. 192 см2.
. 3.2. 192 см2.
23.3. 64p см2; 100p см2. 23.4. 510p см2. 23.5.  .
.
3.6.  3.7. arctg
3.7. arctg  3.8. 2184p см3.
3.8. 2184p см3.
3.9. 23232p см3. 3.10. 
Раздел 11.6
I уровень
1.1. 15 см. 1.2.  см. 1.3. 5 см или 45 см.
см. 1.3. 5 см или 45 см.
1.4. 180p см2 или 720p см2. 1.5. 12p см2.
1.6. В »50 раз. 1.7. 9 см; 7 см. 1.8. 
1.9. В 4 раза.
II уровень
2.1. 2 см. 2.2.  см. 2.3. 65 см. 2.4. 36p см2.
см. 2.3. 65 см. 2.4. 36p см2.
2.5. 180p см2. 2.6. 28p см2. 2.7. 300p см2.
2.8.  см2;
см2;  см2.
см2.
2.9. 
 2.10.
2.10. 
III уровень
3.1. 306p. 3.2.  м. 3.3.
м. 3.3. 
3.4.  3.5.
3.5. 
Раздел 11.7
I уровень
1.1. 72. 1.2. 10 см3. 1.3. 16,5p см2. 1.4. 588.
1.5.  1.6.
1.6.  1.7. 640p.
1.7. 640p.
1.8.  1.9.
1.9.  1.10. 6.
1.10. 6.
II уровень
2.1. 9pа2. 2.3.  2.4.
2.4. 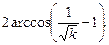
2.5.  2.6.
2.6. 
2.7.  2.8.
2.8. 
2.9.  2.10. 60º.
2.10. 60º.
|
из
5.00
|
Обсуждение в статье: Сфера, вписанная в многогранник или тело вращения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

