Раздел 1. Линейная и векторная алгебра. I. Задания для самостоятельной работы

I. Задания для самостоятельной работы

1. Изучить теоретический материал по теме «матрицы и определители»:

1.1. Матрицы, действия с ними.

1.2. Понятие обратной матрицы.

1.3. Матричная запись системы линейных уравнений.

1.4. Определители второго и третьего порядков, их свойства.

1.5. Алгебраические дополнения и миноры.

1.6. Определители n-го порядка. Вычисление определителя разложением по строке (столбцу).

1.7. Свойства определителей.

1.8. Вычисление обратной матрицы.

2. Изучить теоретический материал по теме «системы линейных алгебраических уравнений:

2.1. Системы трех линейных уравнений.

2.2. Правило Крамера.

2.3. Система n линейных уравнений с n неизвестными.

2.4. Метод Гаусса.

2.5. Метод обратной матрицы.

3. Изучить теоретический материал по теме «Пространство Rⁿ»

3.1. Пространство Rⁿ.

3.2. Линейные операции над векторами.

3.3. Норма в Rⁿ.

3.4. Скалярное произведение в Rⁿ.

3.5. Линейно зависимая и линейно независимая система векторов.

3.6. Условие компланарности трёх векторов в R³.

3.7. Угол между векторами

3.8. Базис.

4. Выполнить задания:

Задача 1

Даны матрицы , , .

1. Вычислить матрицу 4A+5C+7 .

2. Выполняется ли равенство AC=CA?

3. Вычислить определители , , и проверить равенство: = = .

4. Используя свойства определителей, вычислить определитель

 

 

Задача 2

1. Решить систему AX=B матричным методом.

2. Решить системы уравнений по формулам Крамера:

, , .

3. Решить систему уравнений методом Гаусса: .

Задача 3.Даны векторы , = . Вычислить и изобразить в системе координат следующие линейные комбинации векторов и :

, ,

 

Задача 4

Найти линейную комбинацию векторов , = , 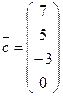с коэффициентами .

Задача 5

 

Будут ли векторы линейно зависимы или линейно независимы в случаях:

а) = = ; б) = = ; в) = = , ?

 

Задача 6

 

Даны три вектора = = , . Доказать, что система образует базис в . Найти разложение вектора по этому базису.

Задача 7.Даны два вектора = и = . Найти угол между векторами и 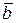, а также .

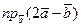Задача 8.При каком значении 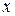вектор = 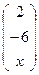ортогонален вектору = ?

 

При каких значениях x и y векторы и параллельны?

 

Задача 9

 

Вычислить площадь и высоту треугольника с вершинами A(7;3;4), B(1;0;6) и C(4;5;7).

 

Задача 10

 

Вершины треугольной пирамиды находятся в точках , , и . Вычислить: а) объем пирамиды; б) высоту, опущенную из вершины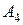

Задача 11

Выяснить, лежат ли точки D(1;0;1), E(0;1;–3)в плоскости ABC, где A(5;–3;0), B(–4;3;3), C(–4;2;4).

II. Контрольные вопросы для самопроверки

1. Что называют матрицей?

2. Как определяются сумма матриц, умножение матрицы на действительное число?

3. Какие матрицы можно перемножать и каким образом?

4. Что такое невырожденная матрица?

5. Как вычислить определитель второго, третьего порядков?

6. Как найти обратную матрицу для данной вырожденной квадратной матрицы?

7. Что такое ранг матрицы?

8. В чем заключается правило Крамера для решения линейных систем?

9. Как с помощью обратной матрицы решить систему линейных уравнений?

10. Для решения каких систем применим метод обратной матрицы?

11. Для решения каких систем применяют метод Гаусса?

12. Что такое прямой и обратный ход метода Гаусса?

13. Как определяется скалярное произведение в пространстве Rⁿ?

14. Как определяется норма в Rⁿ?

15. Какие векторы называются линейно зависимыми?

16. Какие векторы в Rⁿ образуют базис?

17. В чем состоит критерий базисности?

18. Как определить угол между векторами в Rⁿ?