 |
Главная |
МГНОВЕННЫЙ ЦЕНТР ВРАЩЕНИЯ. ЦЕНТРОИДЫ
|
из
5.00
|
Для двух бесконечно близких положений плоской фигуры вместо центра конечного вращения получим так называемый мгновенный центр вращения. Любое плоское перемещение фигуры можно приближенно заменить последовательностью вращательных перемещений вокруг своих центров конечного вращения. В пределе плоское перемещение фигуры можно заменить бесконечной последовательностью элементарных мгновенных поворотов вокруг мгновенных центров вращений, расположенных в определенной последовательности.
Отсюда следует, что любое плоское движение фигуры можно заменить последовательностью мгновенных вращений, совершаемых за тот же промежуток времени, что и рассматриваемое плоское движение. Можно ввести угловую скорость вращения вокруг мгновенного центра вращения или, точнее, вокруг мгновенной оси, проходящей через мгновенный центр вращения и перпендикулярной плоскости движения.
При плоском движении фигуры мгновенный центр вращения перемещается как в неподвижной, так и в подвижной плоскости, скрепленной с движущейся плоской фигурой. Геометрическое место мгновенных центров вращения на неподвижной плоскости называют неподвижной центроидой, а геометрическое место этих же мгновенных центров вращения на подвижной плоскости, скрепленной с движущейся фигурой, – подвижной центроидой. Для каждого плоского движения фигуры существуют свои две центроиды: подвижная и неподвижная. Очевидно, что точка плоской фигуры, с которой в рассматриваемый момент совпадает мгновенный центр вращения, имеет скорость, равную нулю; следовательно, она является в то же время мгновенным центром скоростей.
 При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной центроиде. Эта теорема позволяет плоское движение твердого тела рассматривать как качение без скольжения одной плоской кривой по другой.
При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной центроиде. Эта теорема позволяет плоское движение твердого тела рассматривать как качение без скольжения одной плоской кривой по другой.
 Центроиды нашли применение в некоторых вопросах кинематики механизмов. В общем случае движения плоской фигуры мгновенный центр скоростей – точка
Центроиды нашли применение в некоторых вопросах кинематики механизмов. В общем случае движения плоской фигуры мгновенный центр скоростей – точка 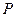 – и мгновенный центр ускорений – точка
– и мгновенный центр ускорений – точка  – являются различными точками этой фигуры (рис. 51). Эти точки совпадают, если плоское движение вырождается во вращательное движение вокруг неподвижной оси.
– являются различными точками этой фигуры (рис. 51). Эти точки совпадают, если плоское движение вырождается во вращательное движение вокруг неподвижной оси.
Выберем точку 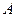 плоской фигуры и отметим точки
плоской фигуры и отметим точки 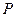 и
и  . Поставим задачу – указать формулы, по которым можно вычислить проекции ускорения точки
. Поставим задачу – указать формулы, по которым можно вычислить проекции ускорения точки 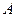 на оси
на оси  и
и  ,
,  и
и  . Ось
. Ось  перпендикулярна оси
перпендикулярна оси  и
и 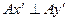 . Точка
. Точка  является мгновенным центром ускорений. Следовательно, ускорение
является мгновенным центром ускорений. Следовательно, ускорение  и направлено всегда к точке
и направлено всегда к точке  ; проекция ускорения на перпендикулярное направление
; проекция ускорения на перпендикулярное направление 
 .
.
Точка 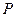 является мгновенным центром скоростей. Скорость точки
является мгновенным центром скоростей. Скорость точки 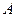 перпендикулярна
перпендикулярна 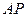 , а скорость всегда направлена по касательной к траектории. Следовательно, ось
, а скорость всегда направлена по касательной к траектории. Следовательно, ось  есть касательная к траектории и проекция ускорения на нее является касательным ускорением и вычисляется по формуле для касательного ускорения
есть касательная к траектории и проекция ускорения на нее является касательным ускорением и вычисляется по формуле для касательного ускорения
 .
.
Ось  перпендикулярна касательной; следовательно, это главная нормаль траектории. Проекция ускорения на это направление вычисляется по формуле для нормального ускорения
перпендикулярна касательной; следовательно, это главная нормаль траектории. Проекция ускорения на это направление вычисляется по формуле для нормального ускорения  . Если
. Если  , то траектория точки обращена выпуклостью к точке
, то траектория точки обращена выпуклостью к точке 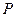 , если
, если  , то вогнутостью.
, то вогнутостью.
Кажется, что у точки 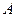 два различных нормальных и касательных ускорения. Но
два различных нормальных и касательных ускорения. Но  и
и  – касательное и нормальное ускорения абсолютного движения точки
– касательное и нормальное ускорения абсолютного движения точки 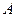 по отношению к неподвижной системе координат (на рис. 51 не показана), а
по отношению к неподвижной системе координат (на рис. 51 не показана), а  и
и  – соответственно касательное и нормальное ускорения относительного движения точки
– соответственно касательное и нормальное ускорения относительного движения точки 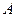 по отношению к подвижной системе координат, движущейся поступательно относительно неподвижной вместе с точкой
по отношению к подвижной системе координат, движущейся поступательно относительно неподвижной вместе с точкой  . Переносное ускорение точки
. Переносное ускорение точки 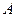 совпадает с абсолютным ускорением точки
совпадает с абсолютным ускорением точки  , а оно равно нулю, так как эта точка фигуры является мгновенным центром ускорений.
, а оно равно нулю, так как эта точка фигуры является мгновенным центром ускорений.
4. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТЕЛА
Вращением твердого тела вокруг неподвижной точки называют такое движение, при котором одна точка тела остается все время неподвижной. Это вращение часто называют сферическим движением твердого тела в связи с тем, что траектории всех точек тела при таком движении располагаются на поверхностях сфер, описанных из неподвижной точки. Одной из главных задач при изучении вращения тела вокруг неподвижной точки является установление величин, характеризующих это движение, т.е. углов Эйлера, угловой скорости, углового ускорения, и вывод формул для вычисления скоростей и ускорений точек тела.
|
из
5.00
|
Обсуждение в статье: МГНОВЕННЫЙ ЦЕНТР ВРАЩЕНИЯ. ЦЕНТРОИДЫ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

