УСКОРЕНИЯ ТОЧЕК ТЕЛА ПРИ ВРАЩЕНИИ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ

Формулу для ускорения какой-либо точки тела, вращающегося вокруг неподвижной точки, нельзя получить непосредственно используя формулу для ускорения при вращательном движении вокруг неподвижной оси, так как в рассматриваемом случае угловое ускорение в общем случае не направлено по оси вращения, а следовательно, и по 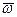. Во всем остальном формулы для ускорения в этих случаях полностью аналогичны.

Формулу для ускорения какой-либо точки тела М можно получить путем дифференцирования по времени вектора скорости, учитывая, что скорость вычисляют по формуле (97). Выполняя это дифференцирование, получаем

.

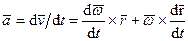Так как

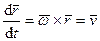, , то

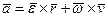. (103)

Формулу (103) часто называют формулой Ривальса.

Часть общего ускорения точки

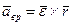(104)

называют вращательным ускорением, а другую часть

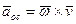(105)

осестремительным ускорением. Следовательно, формула (103) примет вид

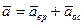. (106)

т.е. ускорение точки тела, вращающегося вокруг неподвижной точки, равно векторной сумме вращательного и осестремителъного ускорений.

В общем случае вращательное и осестремительное ускорения не перпендикулярны; следовательно, модуль ускорения а вычисляют как диагональ параллелограмма по формуле

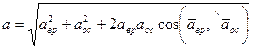. (107)

Рассмотрим вращательное и осестремительное ускорения по отдельности. Вращательное ускорение вычисляют по формуле (104), аналогичной формуле (97) для скорости точки. Только здесь вместо угловой скорости 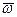входит угловое ускорение . Поэтому вращательное ускорение 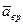направлено аналогично скорости 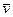, если тело вращается в рассматриваемый момент времени с угловой скоростью, равной угловому ускорению .

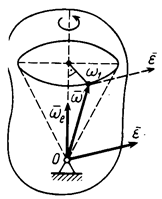Модуль вращательного ускорения 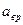определяют аналогично модулю скорости 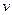(см. формулу (98)):

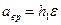, (108)

где 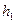– кратчайшее расстояние от точки тела до линии, по которой направлено угловое ускорение 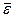(рис. 57).

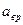Формула (108) для получается из (104):

,

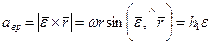где .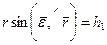

Из (108) следует, что вектор углового» ускорения расположен на прямой линии, проходящей через неподвижную точку. В противном случае эта точка имела бы не равное нулю вращательное ускорение.

Модуль осестремительного ускорения 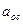можно получить из формулы (105):

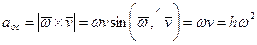, (109)

т. к. угловая скорость 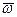перпендикулярна скорости .

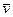Осестремительное ускорение направлено по перпендикуляру к мгновенной оси, опущенному из точки, для которой оно вычисляется, т.е. по отрезку 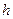, так как, являясь векторным произведением 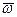и 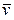, оно перпендикулярно плоскости, где находятся эти векторы, и имеет направление вектора этого векторного произведения. Если ввести вектор , направленный по перпендикуляру от мгновенной оси к рассматриваемой точке, то

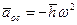. (110)

В случае вращения твердого тела вокруг неподвижной оси угловое ускорение и угловая скорость направлены по этой оси; тогда расстояния 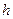и 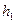равны. Следовательно, вращательное ускорение превращается в касательное ускорение, а осестремительное – в нормальное или центростремительное ускорение.

Таким образом, вращение тела вокруг неподвижной точки можно рассматривать как более общее движение, чем вращение тела вокруг неподвижной оси.