Сложение вращений вокруг пересекающихся осей

Пусть твердое тело участвует одновременно в двух вращениях: переносном с угловой скоростью 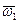и относительном с угловой скоростью . Оси вращений пересекаются в точке 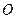(рис. 68). Векторы угловых скоростей как скользящие векторы можно считать перенесенными в точку 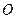осей вращения.

Примером тела, участвующего в двух вращениях вокруг пересекающихся осей, является диск 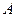, свободно насаженный на ось и вращающийся вокруг нее с угловой скоростью . Вместе с осью диск еще вращается вокруг другой оси (рис. 69) с угловой скоростью .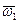

Определим вид движения твердого тела, участвующего в двух вращениях вокруг пересекающихся осей. Точка 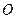тела, расположенная на пересечении осей вращения, является неподвижной, и ее абсолютная скорость . Докажем, что любая другая точка тела, находящаяся на диагонали параллелограмма, построенного на векторах угловых скоростей и , тоже имеет в рассматриваемый момент скорость, равную нулю.

По теореме о сложении скоростей для точки имеем:

.

Так как переносное и относительное движения являются вращениями вокруг осей, то

, ,

где – кратчайшие расстояния от точки до соответствующих осей вращения. Площади треугольников в параллелограмме равны, поэтому 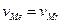. Векторы скоростей и 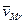имеют противоположные направления. Таким образом, . Это справедливо для любой точки , расположенной на диагонали параллелограмма, так как масштаб векторов можно изменять. Точки оси имеют скорости, равные нулю. Следовательно, является мгновенной осью вращения тела в рассматриваемый момент, т.е. при сложении двух вращений вокруг пересекающихся осей, одно из которых переносное, а другое – относительное, получается вращение тела вокруг мгновенной оси.

Для определения абсолютной угловой скорости вращения вокруг мгновенной оси выберем на теле точку 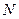и вычислим ее скорость один раз как скорость сложного движения, а другой – как вращения вокруг мгновенной оси. По формуле Эйлера для вращательных движений при сложном движении имеем

.

Для абсолютного вращения вокруг мгновенной оси

.

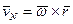Приравнивая скорости, получаем

, (137)

т.е. угловая скорость абсолютного вращения равна векторной сумме угловых скоростей составляющих вращений.

Последовательное применение этого правила сложения вращений вокруг пересекающихся осей позволяет заменить любое количество вращений вокруг пересекающихся осей одним вращением, угловая скорость которого 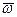равна векторной сумме угловых скоростей составляющих вращений:

.

Тело, участвующее в двух вращениях вокруг пересекающихся осей, имеет неподвижную точку, расположенную на пересечении осей. Оно вращается вокруг неподвижной точки, т.е. совершает сферическое движение. Таким образом, сферическое движение твердого тела можно считать состоящим из двух вращений вокруг пересекающихся осей: переносного и относительного.

Сферическое движение совершает конус 2 при качении без скольжения по неподвижному конусу 1 (рис. 70). Его движение можно считать двумя вращениями вокруг пересекающихся осей. Относительное вращение происходит вокруг оси подвижного конуса с угловой скоростью , а переносное – вокруг оси неподвижного конуса с угловой скоростью . Абсолютным движением является вращение вокруг мгновенной оси 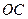с угловой скоростью

.

Мгновенная ось 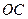, как и ось подвижного конуса , вращается вокруг оси неподвижного конуса с угловой скоростью .

От движения подвижного конуса по неподвижному без скольжения легко перейти к движению подвижной конической шестерни по неподвижной шестерне, если у конусов отрезать их части плоскостями, перпендикулярными осям и .