 |
Главная |
Бесконечно малые и бесконечно большие величины
|
из
5.00
|
Предел функции в точке
Пусть функция 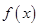 определена в некоторой окрестности точки
определена в некоторой окрестности точки 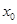 ,кроме, быть может, самой точки
,кроме, быть может, самой точки 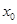 .
.
Число  называется пределом функции
называется пределом функции 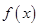 при
при  , стремящемся к
, стремящемся к 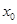 (записывается
(записывается  ), если для любого сколь угодно малого числа
), если для любого сколь угодно малого числа 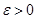 найдется такое число
найдется такое число  (вообще говоря, зависящее от
(вообще говоря, зависящее от 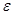 ), что для всех
), что для всех  таких, что
таких, что  ,
,  , выполняется неравенство
, выполняется неравенство  . Предел функции
. Предел функции 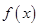 обозначается так:
обозначается так:  .
.
Предел функции на бесконечности
Пусть функция f(x) определена на бесконечном промежутке  . Число А называется пределом функции
. Число А называется пределом функции 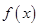 при x стремящемся к бесконечности (записывается
при x стремящемся к бесконечности (записывается 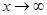 ) если для любого числа e > 0 найдется такое число
) если для любого числа e > 0 найдется такое число  , что для всех значений
, что для всех значений  имеет место неравенство | f(x) – А| < e.
имеет место неравенство | f(x) – А| < e.
Если число А является пределом функции f(x) при  , стремящемся к бесконечности, то пишут
, стремящемся к бесконечности, то пишут 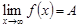 .
.
Операции над пределами
Пусть функции 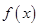 и
и  определены в некоторой окрестности точки х0 и имеют пределы
определены в некоторой окрестности точки х0 и имеют пределы  ,
,  . Перечислим без доказательства свойства пределов от суммы (разности), произведения и частного этих функций.
. Перечислим без доказательства свойства пределов от суммы (разности), произведения и частного этих функций.
1. Предел суммы (разности) этих функций равен сумме (разности) их пределов:
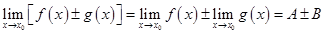
2. Предел произведения функций равен произведению их пределов:
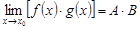 .
.
Отсюда, в частности, вытекает, что постоянный множитель можно выносить за знак предела функции:

3. Предел частного функций равен частному их пределов (при условии В ¹0):
 .
.
Пример 1.1  =
=
= 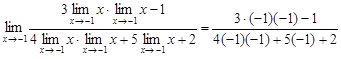 = 2.
= 2.
Из этого примера следует, что указанный предел может быть найден, если в выражение  подставить значение
подставить значение  .
.
Пример 1.2
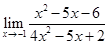 . Аналогично предыдущему примеру, нетрудно убедиться, что
. Аналогично предыдущему примеру, нетрудно убедиться, что 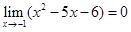 , а
, а  =11,
=11,
поэтому  .
.
Бесконечный предел
Пусть функция 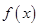 определена в некоторой окрестности точки
определена в некоторой окрестности точки 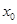 ,кроме быть может, самой точки x0.
,кроме быть может, самой точки x0.
Говорят, что  =¥ (предел функции
=¥ (предел функции 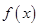 равен бесконечности), если для любого сколь угодно большого числа
равен бесконечности), если для любого сколь угодно большого числа  найдется такое число
найдется такое число  (вообще говоря, зависящее от М ), что для всех
(вообще говоря, зависящее от М ), что для всех  таких, что
таких, что  ,
,  , выполняется неравенство
, выполняется неравенство 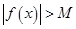 .
.
Бесконечно малые и бесконечно большие величины
Бесконечно малая. Функция 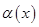 называется бесконечно малой величиной (или просто бесконечно малой) при
называется бесконечно малой величиной (или просто бесконечно малой) при  (или
(или 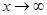 ), если
), если
 ( или
( или  )
)
Например,  – бесконечно малая при
– бесконечно малая при  ,
,  – бесконечно малая при
– бесконечно малая при  , функция
, функция 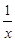 – бесконечно малая при
– бесконечно малая при 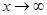 .
.
Бесконечно малые функции будем обозначать 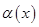 ,
, 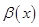 ,
,  , . . . (или просто
, . . . (или просто 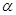 ,
,  ,
,  , . . . ).
, . . . ).
Бесконечно большая. Функция  называется бесконечно большой величиной (или просто бесконечно большой) при
называется бесконечно большой величиной (или просто бесконечно большой) при  (или
(или 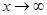 ), если
), если
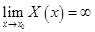 ( или
( или  )
)
Бесконечно большие функции будем обозначать  ,
,  ,
,  , . . . (или просто
, . . . (или просто 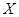 ,
,  ,
,  , . . . ).
, . . . ).
В дальнейшем, вместо слов “бесконечно малая” будем иногда писать БМ, а вместо слов “бесконечно большая” – ББ.
Между бесконечно малыми и бесконечно большими существует связь. Если функция 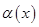 – БМ при
– БМ при  , то функция
, то функция 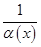 – ББ при
– ББ при  . И наоборот, если функция
. И наоборот, если функция  является ББ при
является ББ при  , то функция
, то функция 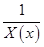 – БМ при
– БМ при  .
.
Например, 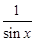 – бесконечно большая при
– бесконечно большая при  ,
,  – бесконечно большая при
– бесконечно большая при  , а функция
, а функция  – бесконечно большая при
– бесконечно большая при 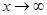 .
.
Другими словами, деление конечной величины на бесконечно малую в результате дает бесконечно большую.
Пример 1.3.
Найдем  .Не трудно убедиться, что числитель этой дроби стремится к 11, а знаменатель стремится к 0 (см. пример 1.2), поэтому
.Не трудно убедиться, что числитель этой дроби стремится к 11, а знаменатель стремится к 0 (см. пример 1.2), поэтому  =
= 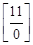 =
=  .
.
Здесь (и в дальнейшем) запись в квадратных скобках 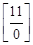 означает, что знаменатель этой дроби не равен 0, а только стремится к этому значению (соответственно и числитель не равен, а только стремится к 11).
означает, что знаменатель этой дроби не равен 0, а только стремится к этому значению (соответственно и числитель не равен, а только стремится к 11).
|
из
5.00
|
Обсуждение в статье: Бесконечно малые и бесконечно большие величины |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

