 |
Главная |
Основные свойства б.м. и б.б. последовательностей
|
из
5.00
|
Вопросы к экзамену по математическому анализу (первый семестр).
1. Числовая последовательность. Операции над последовательностями.
a. Последовательностью называется функция, которая переводит множество натуральных чисел  в некоторое множество
в некоторое множество 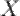 :
: 
Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения. В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому правилу. Например, известен первый член  последовательности и известно, что
последовательности и известно, что  , то есть
, то есть  и так далее до нужного члена.
и так далее до нужного члена.
2. Виды последовательностей. Ограниченные, неограниченные, стационарные последовательности. Предел последовательности. Теоремы о единственности предела последовательности (доказательство).
Если у последовательности  существует конечный предел
существует конечный предел  , то она называется сходящейся (в частности, бесконечно малой при
, то она называется сходящейся (в частности, бесконечно малой при

). В противном случае – расходящейся, при этом возможны два варианта: либо предела вовсе не существует, либо он бесконечен. В последнем случае последовательность называют бесконечно большой. Пронесёмся галопом по примерам первого параграфа:
Последовательность  называется ограниченной сверху, если существует такое число
называется ограниченной сверху, если существует такое число  , что для любого номера
, что для любого номера 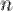 ,
, 
Последовательность  называется ограниченной снизу, если существует такое число
называется ограниченной снизу, если существует такое число  , что для любого номера
, что для любого номера 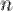 ,
, 
Последовательность  называется ограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число
называется ограниченной, если она ограниченная сверху и ограниченная снизу, то есть существует такое число  , что для любого номера
, что для любого номера 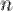 ,
, 
Последовательность  называется неограниченной, если существует такое число
называется неограниченной, если существует такое число  , что существует такой номер
, что существует такой номер 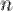 , что
, что 
Число 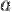 называется пределом последовательности
называется пределом последовательности  и обозначается
и обозначается  ,
, 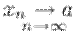
Число 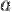 называется пределом последовательности
называется пределом последовательности  , если для любого
, если для любого  существует номер
существует номер 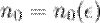 такой, что для любого
такой, что для любого 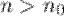 выполняется неравенство
выполняется неравенство  :
:

3. Бесконечно малые и бесконечно большие последовательности. Свойства.
Последовательность  называется бесконечно малой последовательностью (б.м.п.), если для любого
называется бесконечно малой последовательностью (б.м.п.), если для любого  существует номер
существует номер 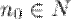 такой, что для любого
такой, что для любого  выполняется неравенство:
выполняется неравенство: 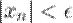
Последовательность  называется бесконечно большой (б.б.п.), если для любого
называется бесконечно большой (б.б.п.), если для любого 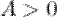 существует номер
существует номер 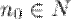 такой, что для любого
такой, что для любого  выполняется неравенство:
выполняется неравенство: 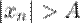
Основные свойства б.м. и б.б. последовательностей
1° Сумма б.м. последовательностей есть б.м.п.
2° Произведение ограниченной последовательности и б.м. есть б.м.п.
3° Если  - б.м.п., то
- б.м.п., то  - ограниченная последовательность.
- ограниченная последовательность.
4° Произведение б.м.п. есть последовательность б.м.
5° Если  - б.м.п. и
- б.м.п. и  , то
, то 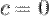 , т.е.
, т.е. 
6° Если  - б.м.п. и
- б.м.п. и  , то последовательность
, то последовательность 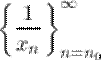 - б.б.п.
- б.б.п.
7° Если  - б.б.п., то
- б.б.п., то 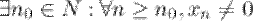 и последовательность
и последовательность 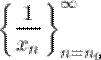 - б.м.п.
- б.м.п.
4. Предел функции в точке и на бесконечности. Односторонние пределы. Основные свойства пределов числовых функций.
Пусть задано некоторое числовое множество  и каждому
и каждому  поставлено в соответствие число
поставлено в соответствие число  , тогда говорят, что на множестве
, тогда говорят, что на множестве 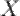 задана функция
задана функция  ,
,  .
.
|
из
5.00
|
Обсуждение в статье: Основные свойства б.м. и б.б. последовательностей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

