Квазистационарные токи

При рассмотрении электрических колебаний приходится иметь дело с токами, изменяющимися со временем. До сих пор мы рассматривали законы постоянного тока (глава 4). Однако они оказываются справедливыми и для изменяющихся (переменных) токов, если только изменение силы тока происходит не слишком быстро. Если изменения тока настолько медленны, что за время установления электрического равновесия в цепи относительные изменения токов и ЭДС малы, то мгновенные значения токов и ЭДС будут подчиняться всем законам постоянного тока. Такие токи называют медленно меняющимися или квазистационарными. Для квазистационарного тока мгновенные значения тока оказывается практически одинаковыми на всех участках цепи.

Отметим, что скорость установления электрического равновесия весьма велика, и поэтому под понятие квазистационарных токов подпадают в обычном смысле весьма быстрые процессы. Все технические переменные токи являются квазистационарными. Даже очень быстрые электрические колебания, употребляемые в радиотехнике, с частотами порядка миллиона колебаний в секунду, очень часто можно рассматривать как квазистационарные.

Из сказанного следует, что задачи на квазистационарные электрические процессы можно решать при помощи законов постоянных токов, если применять эти законы к мгновенным значениям электрических величин. Однако при этом вместо алгебраических соотношений мы приходим к дифференциальным уравнениям, интегрирование которых и дает зависимость искомых величин от времени.

Чтобы процесс был квазистационарным, необходимо выполнение двух условий. Первое условие относится к процессам внутри проводника. Если в проводящей среде возник избыточный объемный заряд с плотностью r, то этот заряд под действием вызванного им самим поля будет уменьшаться с течением времени по закону:

 

r = r₀×exp(-t/t_М). (44.1)

 

В (44.1) r₀ – объемная плотность заряда в момент времени t = 0, а

 

t_М = ee₀/s, (44.2)

 

где e - диэлектрическая проницаемость среды, s - ее удельная электропроводность.

Время t_М называется временем релаксации Максвелла. Оно равно времени, в течение которого объемный заряд уменьшается в е = 2,72 раза. Следовательно, время релаксации Максвелла, определяет порядок величины времени, в течение которого восстанавливается стационарность электрических процессов. Чтобы токи можно было считать квазистационарными, характерное время рассматриваемого неустановившегося процесса Т должно удовлетворять условию:

 

t_М << Т. (44.3)

 

Если токи изменяются периодически (электрические колебания), то под Т следует понимать период колебаний и сформулированное условие квазистационарности примет вид:

nt_М << 1, (44.4)

 

где n = 1/Т – частота колебаний.

Для изоляторов время релаксации Максвелла t_М ~ минуты, для металлов t_М ~ 10^-17 с.

Второе условие накладывается на размеры контура l. Дело в том, что при любом изменении электрического состояния в какой-либо части контура электрические возмущения распространяются вдоль контура с конечной скоростью, равной (глава 8):

 

v = c/ .

 

Здесь c » 3×10⁸ м/с скорость света в вакууме, а e и m - диэлектрическая и магнитная проницаемости среды, окружающей проводники. Если l – длина контура, то время прохождения электромагнитного возмущения вдоль контура равно

t = l/v = (l/c) . (44.5)

 

Для периодически изменяющихся токов условие квазистационарности будет выполнено, если

t << Т, или nt_М << 1, (44.6)

 

где Т – период изменений тока, n = 1/Т – частота колебаний.

В металлах v ~ c, и при размерах контура l =3 м, время t ~ 10^-8 с. Поэтому для этого контура токи можно считать квазистационарными вплоть до частот 10⁶ Гц (это соответствует периоду Т = 10^-6 с).

В зависимости от свойств проводников одно из условий квазистационарности обычно гораздо сильнее другого, и поэтому лишь одно из них является определяющим. При изучении этой главы токи будем считать квазистационарными. Это позволит нам использовать формулы, полученные в статических полях. В частности, закон Ома для мгновенных значений квазистационарных токов.

Колебательный контур

Неразрывная связь между электрическими и магнитными явлениями заключается в том, что любое изменение электрического поля порождает вихревое магнитное поле, а любое изменение магнитного поля приводит в свою очередь к появлению вихревого электрического поля. По этой причине электрические и магнитные колебания могут существовать только совместно, и такие колебания называют электромагнитными колебаниями. При электромагнитных колебаниях периодически изменяющимися величинами являются параметры электрического и магнитного полей.

Для возбуждения и поддерживания электромагнитных колебаний используют колебательный контур – цепь, состоящую из последовательно включенных катушки индуктивностью L и конденсатора емкостью С (см. рисунок 54). Электромагнитные колебания, происходящие в колебательном контуре за счет первоначально сообщенной этому контуру энергии, которая в дальнейшем не пополняется, называют свободными (собственными) электромагнитными колебаниями. Собственные электромагнитные колебания происходят под действием процессов, происходящих в самом колебательном контуре. Если пренебречь сопротивлением проводов катушки индуктивности (R » 0), то можно пренебречь потерями на выделение тепла Джоуля-Ленца. Если к тому же не учитывать незначительные потери энергии на излучение электромагнитных волн в окружающее пространство, то мы имеем незатухающие электромагнитные колебания в контуре.

Рассмотрим превращения энергии в колебательном контуре при свободных незатухающих электромагнитных колебаниях. Предположим, что, разомкнув контур, зарядили конденсатор. Между обкладками конденсатора появляется электрическое поле, которое обладает определенной энергией. Замкнем конденсатор на катушку. В этот момент времени (t = 0) напряженность электрического поля Е₀ между обкладками конденсатора, напряжение U₀ между обкладками и заряд q₀ на обкладках конденсатора максимальны. Тока в контуре еще нет, следовательно, отсутствует и магнитное поле. При этом вся энергия W колебательного контура сосредоточена в виде энергии электрического поля в конденсаторе, т.е. W = .

Когда конденсатор начинает разряжаться, напряжение на нем и напряженность электрического поля между обкладками будут уменьшаться. Из-за возникшего в контуре электрического тока разряда конденсатора в катушке индуктивности появится магнитное поле. При этом согласно правилу Ленца в катушке возникает ЭДС самоиндукции, препятствующая мгновенному нарастанию этого тока. Через время, равное четверти периода колебаний (t = ) конденсатор полностью разряжается (U = 0; E = 0), а сила тока I₀ в контуре и индукция магнитного поля В₀ этого тока достигают максимальных значений. В этот момент времени вся энергия контура заключена в виде энергии магнитного поля в катушке индуктивности, т.е. W = .

В интервале времени от до магнитное поле будет уменьшаться. Уменьшающееся магнитное поле вызывает экстраток самоиндукции, который в соответствии с правилом Ленца стремится поддержать ток разряда конденсатора и будет направлен так же, как и ток разряда. Конденсатор начинает перезаряжаться и между его обкладками появится электрическое поле противоположного направления. Это поле стремится ослабить ток, который в момент времени t = обратится в нуль, а заряд q₀ на обкладках конденсатора (соответственно, напряженность электрического поля Е₀ и напряжение U₀) достигает первоначального максимального значения.

В интервале времени от до конденсатор будет снова разряжаться. При этом в контуре возникает ток, направленный противоположно току в предыдущей стадии процесса. В момент времени t = конденсатор полностью разряжается, т.е. напряжение U между его обкладками становится равным нулю (соответственно, q = 0 и Е = 0), а ток I₀ и индукция В₀ магнитного поля достигают максимальных значений. В этот момент вся энергия электрического поля снова превращается в энергию магнитного поля.

В интервале времени от до Т возникшая в катушке индуктивности ЭДС самоиндукции поддерживает убывающий ток и перезаряжает конденсатор, и через промежуток времени, равный периоду колебаний (t = Т), электрическое состояние контура будет таким же, как и в момент t = 0.

После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора. При отсутствии энергетических потерь процесс взаимных периодических превращений энергий электрического поля и магнитного поля будет продолжаться неограниченно долго, и мы получим незатухающие электромагнитные колебания. При этом в контуре периодически изменяются (колеблются) заряд q на обкладках конденсатора, напряжение U на конденсаторе и сила тока I, текущего через катушку индуктивности.

Для получения уравнения колебаний заряда q в контуре вначале положим, что контур обладает активным сопротивлением R. Тогда согласно закону Ома

 

U_R + U_C = E,

 

где U_R = IR – напряжение на сопротивлении,

U_C = 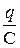- напряжение на конденсаторе,

E = - L = - LI_t¢ = - Lq¢¢_tt , (I = q¢_t, I_t¢ = q¢¢_tt),

Е – ЭДС самоиндукции, возникающая в катушке.

Итак,

 

IR + 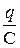= - Lq¢¢,

 

откуда, поделив все слагаемые на L, имеем:

 

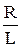q¢¢ + q¢ + 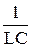q = 0. (45.1)

 

 

Поскольку в колебательном контуре внешние ЭДС отсутствуют, то рассмотренные электромагнитные колебания представляют собой свободные колебания. Если сопротивление контура R = 0, то уравнение (45.1) примет вид:

 

q¢¢ + 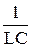q = 0. (45.2)

 

или, обозначая w₀ = 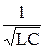, получим

 

q¢¢ + w₀²q = 0. (45.3)

 

Уравнение (45.3) представляет собой дифференциальное уравнение свободных гармонических колебаний заряда в контуре, которое, как легко проверить подстановкой, имеет решение:

q(t) = q₀cos(w₀t + a), (45.4)

 

где q₀ – амплитуда колебаний заряда на обкладках конденсатора, w₀ - циклическая частота колебаний (собственная частота контура), a - начальная фаза.

Период свободных колебаний в идеальном контуре (т.е. при R = 0) равен:

 

Т = = 2p 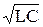. (45.5)

 

Формула (45.5) впервые была получена У. Томсоном и называется формулой Томсона. Частота колебаний

n = 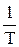= . (45.6)

 

В выражении (45.4) значения амплитуды колебаний заряда q₀ и начальной фазы a определяют из начальных условий, т.е. значениями силы тока I(0) и заряда q(0) (или напряжения U(0) = q(0)/С) в момент времени t = 0.

Напряжение на обкладках конденсатора равно:

 

U_C = U(t) = q(t) = 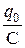cos(w₀t + a) = U₀cos(w₀t + a), (45.7)

 

где U₀ = 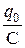- амплитуда колебаний напряжения на конденсаторе.

Сравнивая выражения (45.4) (45.7) убеждаемся, что заряд q(t) и напряжение U(t) колеблются в фазе друг с другом.

Сила тока в колебательном контуре равна:

 

I(t) = I = q¢_t = - w₀q₀sin(w₀t + a) = I₀cos(w₀t + a + ), (45.8)

 

где I₀ = w₀q₀, - амплитуда силы тока.

Сопоставляя выражения (45.4) и (45.8) заключаем, что колебания тока опережает по фазе колебания заряда на , т.е. когда ток достигает максимального значения, заряд равен нулю, и наоборот.

Уравнения (45.4), (45.7), (45.8) для a = 0 записываются так:

 

q(t) = q₀cosw₀t, U_C(t) = U₀cosw₀t, I(t) = I₀cos(w₀t + ),

 

и графики этих зависимостей q(t), U_C(t), I(t) представлены на рисунке 55.

Если в формуле Томсона Т = 2p 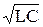индуктивность измерять в генри ([L] = Гн), емкость в фарадах ([С] = Ф), то период колебаний будет измеряться в секундах ([Т] = с).

Из закона сохранения энергии следует, что в идеальном контуре (R = 0) максимальные значения энергии электрического и магнитного полей равны, т.е.

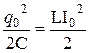, (45.9)

 

откуда с учетом того, что I₀ = w₀q₀, опять приходим к результату

 

w₀² = 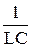. (45.10)

 

Для произвольного момента времени энергии электрического поля и магнитного поля равны, соответственно:

 

W_эл(t) = q²(t) = cos²(w₀t + a) = =

 

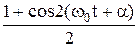= (1 + cos(2w₀t + 2a)), (45.11)

 

W_м(t) = 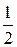LI²(t) = 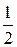LI₀²sin²(w₀t + a) = 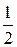LI₀² =

 

= LI₀² (1 -cos(2w₀t + 2a)). (45.12)

 

Из уравнений (45.11) и (45.12) следует, что энергии электрического поля и магнитного поля в контуре изменяются с частотой, в два раза превышающей частоту гармонических электрических колебаний (заряда, силы тока, напряжения) в контуре.

Полная энергия W контура складывается из энергий электрического и магнитного полей и равна максимальному значению энергии электрического или магнитного поля:

W = W_эл(t) + W_м(t) = 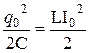. (45.13)

 

Полная энергия W остается постоянной, т. е. неизменной со временем.

Уравнения колебаний энергий электрического поля W_эл(t) и магнитного поля W_м(t), т.е. выражения (45.11) и (45.12), для a=0 с учетом соотношения (45.13) для полной энергии W принимают вид:

 

W_эл(t) = 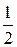W×(1 + cos2w₀t), W_м(t) = 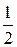W×(1 - cos2w₀t),

 

и графики этих зависимостей W_эл(t) и W_м(t) представлены на рисунке 56.

 

 

Как видно из графиков энергии W_эл(t) и W_м(t) совершают гармонические колебания в противофазе по отношению друг другу около равновесного положения 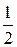W(W – полная энергия контура) с частотой в два раза превышающей частоту гармонических колебаний в контуре.