Равномерное и равнопеременное вращения

Если угловая скорость тела остается во все время движения по­стоянной (ω=const), то вращение тела называется равномерным. Найдем закон равномерного вращения. Из формулы имеем .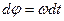

Отсюда, считая, что в начальный момент времени t=0 угол φ=φ₀, и беря интегралы слева от φ₀ до φ, а справа от 0 до t, получим окончательно

.

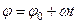Из равенства следует, что при равномерном вращении, когда φ₀=0

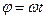и .

В технике скорость равномерного вращения часто определяют числом оборотов в минуту, обозначая эту величину через n об/мин. Найдем зависимость между n об/мин и ω 1/с. При одном обороте тело повернется на угол 2π, а при n оборотах на 2πn; этот поворот делается за время t = 1 мин = 60 сек. Из равенства следует тогда, что

.

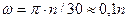Если угловое ускорение тела во все время движения остается постоянным 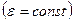, то вращение называется равнопеременным. Найдем закон равнопеременного вращения, считая, что в начальный момент времени t=0 угол 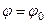, а угловая скорость 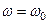( 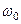- начальная угловая скорость).

Из формулы 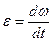имеем 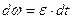. Интегрируя левую часть в пределах от 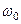до 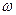, а правую - в пределах от 0 до t, найдем ,

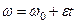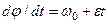или .

Вторично интегрируя, найдем отсюда закон равнопеременного вращения

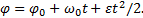
Если величины ω и ε имеют одинаковые знаки, то вращение будет равноускоренным, а если разные – равнозамедленным.

 

Скорости и ускорения точек вращающегося тела.

Установив характеристики движения всего тела в целом, перейдем к изучению движения отдельных его точек.

1. Скорости точек тела. Рассмотрим какую-нибудь точку М твердого тела, находящуюся на расстоянии h от оси вращения (см. рис.9). При вращении тела точка М будет описывать окружность радиуса h, плоскость которой перпендикулярна оси вращения, а центр С лежит на самой оси. Если за время dt проис­ходит элементарный поворот тела на угол dφ, то точка М при этом совершает вдоль своей траектории элементарное перемещение . Тогда числовое значение скорости точки будет равно отно­шению ds к dt, т.е

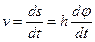или .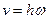

Скорость в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М.

Таким образом, числовое значение скорости точки вращающегося твердого тела равно произведению угловой скорости тела на расстоя­ние от этой точки до оси вращения.

Направлена скорость по касательной к описываемой точкой окружности или перпендикулярно плоскости, проходящей через ось вращения и точку М.

Так как для всех точек тела 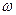имеет в данный момент времени одно и то же значение, то скорости точек вращающегося тела пропорциональны их расстояниям от оси вращения.

 

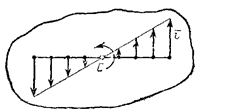
Рис.11 Рис. 12

2. Ускорения точек тела. Для нахождения ускорения точки М воспользуемся формулами , .

В нашем случае ρ=h. Подставляя значение в выражения a_τ и a_n, получим:

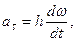
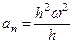
или окончательно:

, .

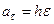Касательная составляющая ускорения a_τ направлена по каса­тельной к траектории (в сторону движения при ускоренном вра­щении тела и в обратную сторону при, замедленном); нормальная составляющая a_n всегда направлена по радиусу МС к оси вращения (рис.12). Полное ускорение точки М будет или .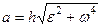

Отклонение вектора полного ускорения от радиуса описываемой точкой окружности определяется углом μ, который вычисляется по формуле 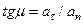. Подставляя сюда зна­чения a_τ и a_n, получаем .

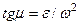Так как ω и ε имеют в данный момент времени для всех точек тела одно и то же значение, то ускорения всех точек вращающегося твердого тела пропорциональ­ны их расстояниям от оси вращения и образуют в данный момент времени один и тот же угол μ с радиусами описываемых ими окруж­ностей. Поле ускорений точек вращающегося твердого тела имеет вид, показанный на рис.14.

 

Рис.13 Рис.14

 

3. Векторы скорости и ускорения точек тела. Чтобы найти выражения непосредственно для векторов v и a, проведем из произвольной точки О оси АВ радиус-вектор 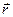точки М (рис. 13). Тогда и по формуле

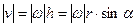или .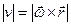

Таким образом, модуль векторного произведения 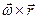равен модулю скорости точки М. Направления векторов 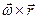и v тоже совпадают (оба они перпендикулярны плоскости ОМВ) и размерно­сти их одинаковы. Следовательно, 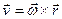- формула Эйлера, т.е. вектор скорости любой точки вращающегося тела равен векторному произведению угловой скорости тела на радиус-вектор этой точки.

Пример 1.Маятник OM качается в вертикальной плоскости так, что . Длина (рис. 15)

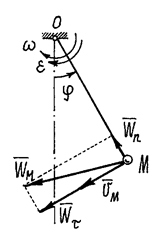
Рис.15

 

Маятник вращается вокруг горизонтальной оси 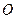, перпендикулярной вертикальной плоскости. Угловая скорость угловое ускорение

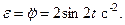
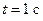
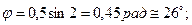
Например, при 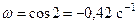(вращение по часовой стрелке); (угловое уско­рение направлено также по часовой стрелке). Вращение в этом положении ускоренное.

Скорость точки : 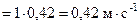(определя­ется модуль скорости). Направлен вектор скорости соответственно направлению угловой скорости – в сторону вращения.

.

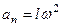
Нормальное ускорение касательное ускорение . (Определён опять модуль вектора ускорения. Направлен вектор вниз, как указывает угловое ускорение).

Величина полного ускорения точки

 

 

Пример 4. Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса.

Дано: ω=20 рад/с , N=10 об.

Найти: ε-?

Решение. При равномерном вращательном движении имеют место следующие два уравнения: φ=φ_о+ω_оt+εt²/2 и ω= ω_о+εt. По условию ω_о=0, тогда эти уравнения примут вид: φ=εt²/2 и ω = εt. Решая их и учитывая, что φ=2πN, получим окончательно ε=ω²/4πN=3,2 рад/с.

Пример 5. Колесо радиусом 10 см вращается с постоянным угловым ускорением 3,14 рад/с² (рис.24). Найти для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость, 2) линейную скорость, 3) тангенциальное ускорение, 4) нормальное ускорение, 5) полное ускорение и 6) угол, составляемый направлением полного ускорения с радиусом колеса.

Дано: R= 0,1 м, ε=3,14 рад/с²

Найти: ω-? v -? a_τ -? a -?

Рис.24

 

Решение. 1) При равнопеременном вращательном движении угловая скорость ω = ω_о+εt. По условию ω_о=0, тогда ω = εt, т.е. ω растет пропорционально времени. К концу первой секунды ω=3,14 рад/с.

2) Так как v=ωR, то линейная скорость также пропорционально времени. К концу первой секунды v = 3,14 м/с.

3) Тангенциальное ускорение a_t=𝜀R не зависит от времени t. В нашем случае a_t=0,314 м/с².

4) Нормальное ускорение a_n=ω²R=ε²t²R, т.е. нормальное ускорение растет пропорционально квадрату времени: при t=1 c a_n=0,986м/с².

5) Полное ускорение растет со временем по закону: a= 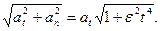При t=1 c a=1,03 м/с².

6) Имеем , где α - угол, составляемый направлением полного ускорения с радиусом колеса. В начальный момент времени, т.е. при t=0, a =a_t - полное ускорение направлено по касательной. При t=∞ a = a_n (так как a_t=const и a_n пропорционально времени), т.е. при t=∞ полное ускорение направлено по нормали. К концу первой секунды sinα=a_t/a_n=0,314/1,03=0,305, т.е. α=17^о46’.

 

Пример 6.Колесо вращается равноускоренно с угловым ускорением ε= 3 рад/с². Определить, какой угловой скорости достигнет тело после t=3 с своего вращения? Сколько оборотов N оно при этом совершит?

Решение.Если тело вращается равноускоренно, то его движение описывает следующая система уравнений

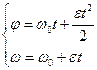
В начальный момент тело покоилось, значит, ω₀=0. Тогда

.

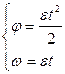Следовательно, ω=εt=3∙3=9 рад/с.

Количество оборотов 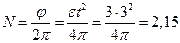оборота.

 

Пример 7.Вентилятор вращался с частотой n₀=900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N=75 об. Какое время t прошло с момента выключения до остановки вентилятора? С каким угловым ускорением ε он двигался?

Решение.Равнозамедленное движение вентилятора описывается следующей системой уравнений

Поскольку вентилятор остановился, то его конечная частота n=0. Тогда выразим 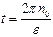из второго уравнения и, подставив его в первое уравнение, а также учитывая, что n₀=900 об/мин = 15 об/с, получим

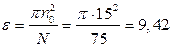рад/с².

Время движения равно с.

 

Пример 8.Точка вращается по окружности радиусом R=20 см с постоянным тангенциальным ускорением a_τ=5 см/с². Через какое время после начала вращения нормальное ускорение точки будет вдвое больше тангенциального?

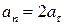Решение.Угловая скорость точки при равноускоренном движении может быть найдена из соотношения ω=ω₀+εt. Так как ω₀=0, то ω=εt. Нормальное ускорение . Тангенциальное ускорение . По условию задачи , тогда 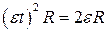, следовательно, и с.

 

Пример 9.Точка движется по окружности радиусом R=2 см. Зависимость пути от времени дается уравнением s(t)=Ct³, где С = 0,1 см/с³. Найти нормальное и тангенциальное ускорения точки в тот момент, когда линейная скорость точки v= 0,3 м/с.

Решение.Зависимость пути от времени позволяет найти зависимости от времени скорости и тангенциального ускорения.

, .

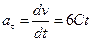Отсюда, с.

Тогда тангенциальное ускорение 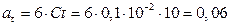м/с².

Нормальное ускорение м/с².

Пример 10.Точка движется по окружности радиусом R = 4 м. Начальная скорость точки равна 3 м/с, тангенциальное ускорение a_τ = 1 м/с². Для момента времени t = 2 с определить: а) длину пути, пройденного точкой, б) модуль перемещения; в) линейную и угловую скорости; г) нормальное, полное и угловое ускорения.

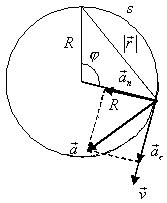
Рис.25

Решение.Уравнение зависимости пути, пройденного точкой, от времени имеет вид (м). Это позволяет найти длину пути 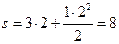м. Если учесть, что за один оборот точка проходит путь, равный длине окружности s₁=2πR=8π м, то можно найти угловое перемещение точки из пропорции 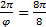, φ=2 (рад) = 114,7⁰. Тогда модуль перемещения может быть найден по теореме косинусов как хорда, стягивающая этот угол φ.

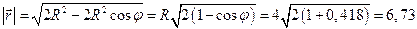м.

Линейная скорость точки м/с.

Угловая скорость рад/с.

Нормальное ускорение 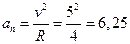м/с².

Полное ускорение . Модуль полного ускорения

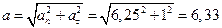м/с².

Угловое ускорение 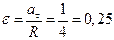рад/с².

Пример 11.Автомобиль, движущийся со скоростью 36 км/ч, проходит закругленное шоссе с радиусом кривизны 200 м. На повороте шофер тормозит машину, сообщая ей ускорение 0,3 м/с². Найти нормальное и полное ускорения автомобиля на повороте. Найти угол между вектором полного ускорения автомобиля на повороте и вектором его скорости. Каковы угловые скорость и ускорение автомобиля в момент вхождения машины в поворот?

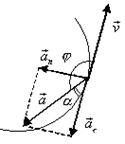
Рис.26

Решение.Зная скорость автомобиля v=36 км/ч =10 м/с, найдем его нормальное ускорение

м/с².

Полное ускорение автомобиля 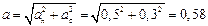м/с².

Угловое ускорение

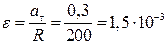рад/с².

Угловая скорость

рад/с.

Поскольку движение автомобиля замедленное, то векторы скорости и тангенциального ускорения направлены в противоположные стороны, поэтому вектор скорости и вектор полного ускорения образуют тупой угол φ. Для нахождения этого угла определим вначале угол α, дополняющий искомый угол до 180⁰.

.

Пример 12.Найти радиус R вращающегося колеса, если известно, что линейная скорость v₁ точки, лежащей на ободе, в 2,5 раза больше линейной скорости v₂, точки, лежащей на расстоянии r =5 cм ближе к оси колеса.

Дано: v₂=2,5v₁, r=R-5

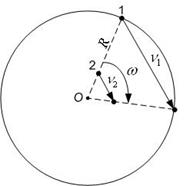
Рис.27

Решение.

1) У точек находящихся на колесе и лежащих на радиусе, будут одинаковы угловые скорости. Используем связь угловой и линейной скоросте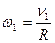й:

и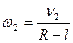

т.к. ω₁=ω₂, приравниваем правые части уравнений:

Решим уравнение относительно R:

; ; ; ;

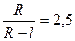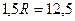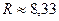
Ответ: Радиус вращающегося колеса равен 8,33 см.

 

 

Вопросы для самопроверки

- Какими кинематическими параметрами характеризуется поступательное движение и почему?

- Запишите уравнение равномерного поступательного движения твердого тела?

- Запишите уравнение равнопеременного поступательного движения твердого тела?

- Запишите уравнение равнопеременного и равномерного вращательного движения твердого тела?

- Почему при поступательном движении тела скорости и ускорения его точек не могут быть различными?

- Приведите определения угловой скорости и углового ускорения тела.

- Как направлены векторы угловой скорости и углового ускорения при вращении тела вокруг неподвижной оси?

- Как вычислить скорость точки тела, вращающегося вокруг неподвижной оси? Объясните куда направлен вектор скорости?

- Запишите формулы для нормального и тангенциального ускорений точки тела, вращающегося вокруг неподвижной оси.

- Перечислите основные виды движений твердого тела.

- Какое движение твердого тела называется поступательным и какими свойствами оно обладает?

- Какое движение твердого тела называется вращением вокруг неподвижной оси и как оно осуществляется?

- По каким формулам определяются модули угловой скорости и углового ускорения вращающегося твердого тела?

- Как направлены векторы угловой скорости и углового ускорения при вращении тела вокруг неподвижной оси?

- Ускорения каких точек вращающегося тела:

а) равны по модулю;

б) совпадают по направлению;

в) равны по модулю и совпадают по направлению?

- Что представляет собой передаточное число передачи и как определяется передаточное число сложной передачи?

- Определите угловую скорость вращения вала электродвигателя (в рад/с), если n=1400 об/мин.? Вычислите скорость и ускорение точки на поверхности вала; диаметр вала d=100 мм?

 

- Определите характер вращения твердого тела вокруг неподвижной оси в следующих случаях:

1) ε=5 рад/с²;

2) ε=0;

3) ω=150 рад/с;

4) ω=20t рад/с, где t – время?

 

- Какая составляющая ускорения любой точки твердого тела равна нулю при равномерном вращении твердого тела вокруг неподвижной оси?

1) нормальное ускорение;

2) касательное ускорение;

3) полное ускорение.