 |
Главная |
Расчет цилиндрических прямозубых колес на прочность по контактным напряжениям
|
из
5.00
|
Целью этого расчета является предотвращение разрушения рабочих поверхностей зубьев вследствие возникновения повторных контактных напряжений сдвига.
В основу расчета зубьев на прочность по контактным напряжениям положена теория статически сжатых цилиндров, разработанная Герцем и развитая Беляевым. Сущность теории Герца-Беляева состоит в следующем. Под действием силы нормального давления FHn на контактных поверхностях двух цилиндров возникают контактные напряжения σH (рис. 4.8).
Величину этих контактных напряжений определяют по формуле
 (4.116)
(4.116)
где  - равномерно распределенная нагрузка, действующая на зубья;
- равномерно распределенная нагрузка, действующая на зубья;
 - приведенный модуль упругости;
- приведенный модуль упругости;
 - приведенный радиус кривизны;
- приведенный радиус кривизны;
μ - коэффициент поперечной деформации (коэффициент Пуассона).
Применим теорию Герца-Беляева для получения основных зависимостей при расчете зубьев прямозубых цилиндрических колес на прочность по контактным напряжениям. Наибольшие контактные напряжения возникают в тот момент, когда точка контакта находится в полюсе зацепления.
Условие прочности зубьев по контактным напряжениям можно в общем виде записать неравенством σH ≤ σHP, где σH – расчетное контактное напряжение; σHP - допускаемое контактное напряжение.
Изобразим зубья шестерни и колеса в тот момент, когда они касаются в полюсе зацепления. Заменим зубья шестерни и колеса цилиндрами с радиусами, равными радиусам кривизны эвольвентных профилей зубьев в точке их касания (рис.4.9).
Согласно свойствам эвольвенты центры заменяющих цилиндров находятся на общей нормали к сопряженным профилям NN в точках А и В, крайних точках линии зацепления АВ.
Радиус кривизны эвольвентного профиля зуба первого колеса:
 (4.117)
(4.117)
Радиус кривизны бокового профиля второго зуба:
 Рис. 4.8
Рис. 4.8
|
 (4.21)
(4.21)
В формулах (4.20) и (4.21) d1 и d2 – делительные диаметры зубчатых колес; u – передаточное число зубчатой передачи.
Приведенный радиус кривизны: 
 Рис. 4.9
Рис. 4.9
|
Приведенный модуль упругости с учетом того, что сопряженные колеса изготовлены из стали, т.е. Е1=Е2.

Выразим равномерно распределенную нагрузку qHn, действующую на зубья через крутящий момент на ведущем звене (шестерне):
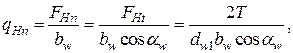
где FHt – окружное усилие; Т1 – крутящий момент на шестерне; bw – ширина зубчатого венца (длина зуба).
Подставим значения qHn, Eio и ρio в формулу Герца-Беляева (4.19):
 (4.22)
(4.22)
Введем следующие обозначения:
Zм – коэффициент, учитывающий механические свойства материалов шестерни и колеса:

Учитывая значения для стальных колес модуля упругости Е=2,1×105 МПа и коэффициента Пуассона μ=0,3, получаем ZM= 275МПа1/2;
ZН – коэффициент, учитывающий форму сопряженных поверхностей зубьев:

Поскольку для некорригированных колес, а также колес с высотной коррекцией, в основном используемых в зубчатых передачах, угол зацепления αw=20°, коэффициент Zн=1,77.
В связи с тем что в процессе работы передачи в зацеплении может находиться не одна пара зубьев, происходит изменение длины контактных линий, учитываемое коэффициентом Zε:

где εα – коэффициент перекрытия.
С учетом введенных коэффициентов формула (4.22) примет вид:
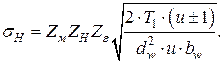 (4.23)
(4.23)
Выразим диаметр начальной окружности шестерни dw1 через межосевое расстояние αw:
 (4.24)
(4.24)
Введем в формулу (4.23) коэффициент нагрузки КН, учитывающий форму сопряженных поверхностей зубьев.

где КНα – коэффициент, учитывающий распределение нагрузки между зубьями. Для прямозубой передачи КНα=1,0;
КНβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого колеса. Коэффициент KHβ зависит от поверхностной твердости зубьев, ширины зубчатого венца и схемы передачи;
КНv – коэффициент динамической нагрузки, зависит от степени точности зубчатых колес, которая назначается в зависимости от окружной скорости.
После подстановки в формулу (4.23) зависимости (4.24), коэффициента КН и приближенных значений коэффициентов Zi=275, ZH =1,77, Zε=1 и преобразований получим следующие выражения расчетов прямозубых зубчатых передач, изготовленных из сталей:
 (4.25)
(4.25)
 (4.26)
(4.26)
Формула (4.25) применяется для проверочных расчетов. Формула (4.26) – для проектных расчетов. В выражениях (4.25), (4.26) приняты следующие обозначения и размерности величин: Т1 – крутящий момент на шестерне, Н·м; аw – межосевое расстояние, мм; σНР, σН – контактные напряжения, МПа; bw2 –ширина колеса, мм; ψba =bw/aw– коэффициент ширины колеса, безразмерная величина. Во всех формулах в сочетании u±1 знак «+» соответствует внешнему зацеплению колес, а знак «-» - внутреннему.
|
из
5.00
|
Обсуждение в статье: Расчет цилиндрических прямозубых колес на прочность по контактным напряжениям |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

