Добротность магнитожидкостной пленки – излучателя упругих колебаний

Магнитожидкостный источник упругих колебаний, функционирующий в мегагерцевом диапазоне частот впервые рассмотрен В.М. Полуниным (1982). Излучатель упругих колебаний представляет собой тонкую магнитожидкостную пленку, нанесенную на поверхность твердого тела. Теоретической моделью данного преобразователя колебаний является бесконечный плоскопараллельный слой МЖ (рисунок 5.7).

Однородная, неэлектропроводная, вязкая МЖ находится на поверхности твердого тела из абсолютно жесткого, немагнитного и неэлектропроводного материала и имеет форму плоскопараллельного слоя толщиной h. Плоскость xoz системы координат совпадает с нижней поверхностью жидкого слоя. На единицу массы жидкости по оси y действует вынуждающая сила

F=f_o×coswt, (5.35)

где w – круговая частота, амплитуда силы f_o не зависит от координат.

Такое выражение для вынуждающей силы можно получить, например, предполагая, что она обусловлена пондеромоторным взаимодействием жидкости с магнитным полем:

H_x=H_o+H_m(y)×coswt, H_y=0 и H_z=0, (5.36)

в котором H_o не зависит от координат, ÑH_m – постоянный по величине вектор, H_m<<H_o. Тогда

f_o=m_oM|ÑH_m|/r. (5.37)

Применительно к данному случаю дифференциальное уравнение колебательного движения имеет следующий вид:

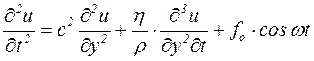, (5.38)

где h=h_v+4h_s/3 – полная вязкость жидкости (h_s и h_v- ее сдвиговая и объемная вязкости).

При неподвижной нижней поверхности жидкого слоя и свободной его верхней поверхности граничные условия имеют вид:

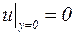и 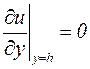. (5.39)

В жидкости установится система плоских стоячих волн:

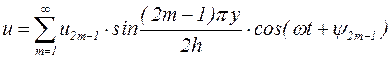. (5.40)

Здесь u_2m-1 – амплитуда смещения частиц жидкости в пучностях 2m–1-й гармоники, а y_2m-1 – сдвиг по фазе между этими смещениями и вынуждающей силой.

Параметры колебательного движения u_2m-1 и y_2m-1 подлежат определению. С этой целью подставим (5.40) в (5.38) и после преобразований получим:

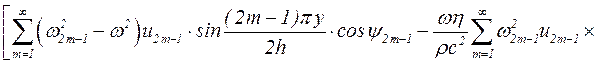
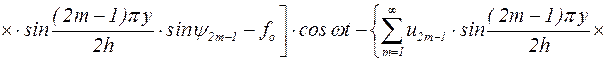
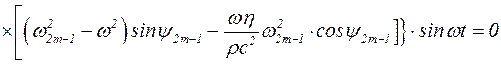, (5.41)

где w_2m-1º(2m-1)pc/2h.

Равенство (5.41) должно выполняться в любой момент времени tи в любой точке y рассматриваемого интервала. Поэтому

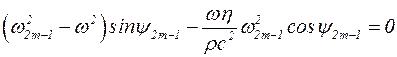, (5.42)

откуда следует 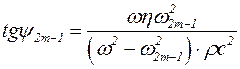. (5.43)

Кроме того, имеем

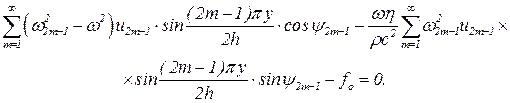...(5.44)

Умножив последний член на тригонометрический ряд 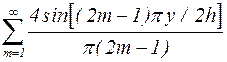, сходящийся к 1 на промежутке 0<y<2h, получим

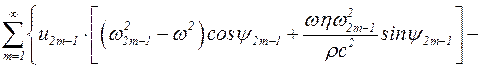
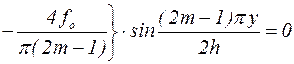. (5.45)

Выражение в фигурных скобках обращается в нуль. Заменяя в нем с помощью известного тригонометрического тождества функции cosy_2m-1 и siny_2m-1 на tgy_2m-1 и воспользовавшись выражением (5.35), получим

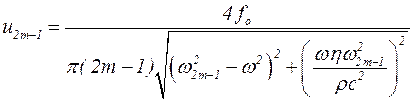. (5.46)

Подстановка (5.46) в (5.40) дает

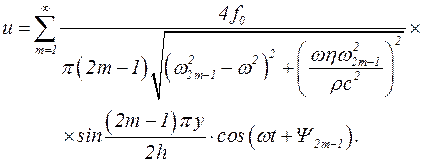(5.47)

Для каждой гармоники может быть записано следующее выражение резонансной частоты :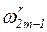

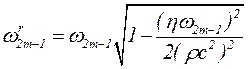. (5.48)

Вследствие малости второго члена в подкоренном выражении

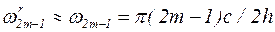. (5.49)

Амплитуда резонансных колебаний 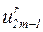при не слишком больших значениях m на несколько порядков превосходит амплитуды соседних гармоник u_2m+1 и u_2m-3 Действительно, используя (5.36), получаем

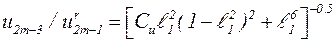(5.50)

и

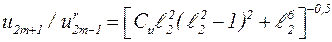, (5.51)

где 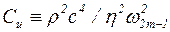; ℓ₁º(2m-3)/(2m-1); ℓ₂º(2m+3)/(2m-1).

Значение h может быть определено по результатам измерения коэффициента поглощения ультразвука a, связанного с h зависимостью a=w²h/2rс³. Воспользовавшись результатами предыдущей главы, будем считать с=1200 м/с, a=200 м^-1 при n=25 МГц. Тогда для m=2: С_u≈10⁵, ℓ₁=1/3, ℓ₂=7/3, u₁/u^r₃»10^-2, u₅/u^r₃»1,3×10^-4. Предположение о малости второго члена в подкоренном выражении (5.38) согласуется с численным значением C_u.

Для частот, близких к резонансной 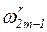, вместо ряда (5.47) можно записать:

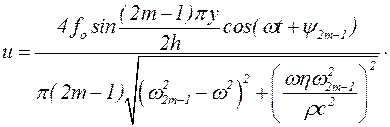(5.52)

При w=w^r_2m-1:

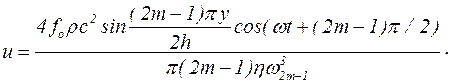(5.53)

Если действует лишь пондеромоторный механизм возбуждения колебаний, то при w»w_2m-1:

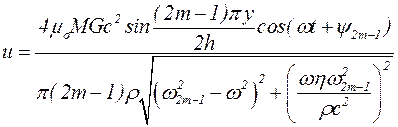. (5.54)

При w=w_2m-1:

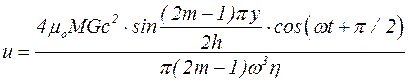. (5.55)

Вид формул (5.43) и (5.52) свидетельствует об аналогии между колебательным движением, совершаемым частицами жидкости, и механической системой с сосредоточенными параметрами, в чем можно убедиться, введя обозначения 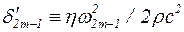и рассматривая эту величину в качестве аналога коэффициента затухания механической системы.

Тогда логарифмический коэффициент затухания Q'_2m-1 и добротность Q'_2m-1 преобразователя с учетом только внутренних потерь могут быть представлены так:

Q'_2m-1=phw_2m-1/rc², (5.56)

Q'_2m-1=rc²/hw_2m-1. (5.57)

Для указанных выше численных значений a и с получаем при m=1: Q'₁=9,5×10^-3 и Q'₁=330.

Акустико-механическая аналогия позволяет произвести расчет амплитуды колебаний частиц при резонансе 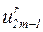с учетом, как внутренних потерь, так и потерь на излучение.

Как известно,

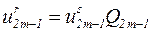, (5.58)

где 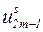– эффективное значение статического смещения.

Имеем

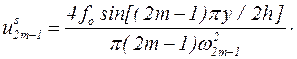(5.59)

Чтобы найти Q_2m-1, воспользуемся свойством аддитивности энергетических потерь за период DW: DW=DW_i+DW_e, где DW_i и DW_e– внутренние потери и потери на излучение за период. Если W – механическая энергия системы в момент времени t, то ее логарифмический коэффициент затухания Q=-0,5|DW|/W. Следовательно,

Q_2m-1=Q'_2m-1+0,5|DW|/W. (5.60)

При выполнении неравенства r_сс_с>>rc (волновое сопротивление твердого тела значительно больше волнового сопротивления жидкости) на границе возникает пучность давления, а через границу проходит плоская ультразвуковая волна с интенсивностью

J=p²/2r_сс_с, (5.61)

где p – амплитуда давления в пучности стоячей волны.

Пренебрегая энергией, излучаемой в воздух, получим

|DW_i|=pp²s/r_сс_сw, (5.62)

где s – площадь активной поверхности жидкого слоя.

Полная энергия жидкого слоя

W=(2m-1)pp²s/8rс. (5.63)

Подставив (5.46) и (5.45) в (5.44), найдем

Q_2m-1=Q'_2m-1+4rс/(2m-1)r_сс_с, (5.64)

а так как Q_2m-1=p/Q_2m-1, то

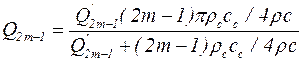. (5.65)

Пусть a и с имеют прежние значения, а r=1200 кг/м³, r_сс_с=133×10⁵ кг/с×м², тогда при m£3 выполняется неравенство 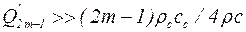, благодаря чему можно записать:

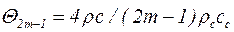и 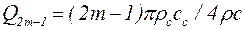. (5.66)

Так, для m=1 получаем Q₁=7,8, что практически совпадает с добротностью кварца, излучающего в воду. Вполне закономерно, что для абсолютно жесткой среды выражение (5.65) дает .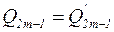

Добротность плоского МЖИ при излучении в твердую среду определяется отношением акустического сопротивления этой среды к акустическому сопротивлению преобразователя – МЖ, тогда как для твердого вибратора, излучающего в жидкость, имеет место обратное отношение.

При «низких» частотах изменения вынуждающей силы, когда w<<w_2m-1, можно говорить о колебаниях «тонкого» слоя МЖ. Для оценки амплитуды колебаний частиц в «тонком» слое жидкости можно воспользоваться эффективным значением статического смещения u_0ef:

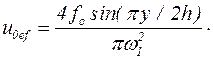(5.67)

Однако формула (3.67) не учитывает вклад гармоник с номерами выше первого. Более точным является выражение, полученное из (5.47) с учетом того, что w<<w₁ и ряд 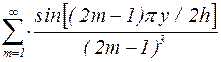сходится в интервале 0£y£2 к функции .

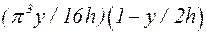Это выражение имеет вид

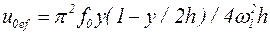. (5.68)