Порядок решения задач на принцип суперпозиции

1.Прочитать задачу; выписать все заданные значения физических величин и перевести их в систему СИ.

2.Сделать рисунок:

· на рисунке изобразить распределение зарядов, которые создают поле;

· выбрать систему координат, учитывая симметрию задачи;

· обозначить все расстояния, которые необходимы для решения задачи, и нарисовать векторы напряженности полей, создаваемых каждым распределением зарядом в интересующей нас точке.

3. Написать формулы для вычисления модулей напряженности полей отдельных зарядов в заданной точке.

4. Спроектировать все векторы напряженностей на оси координат и найти проекции суммарного вектора напряженности на каждую ось. Зная проекции суммарного вектора на оси координат Е_х, Е_y и Е_z, можно вычислить модуль суммарного вектора, используя теорему Пифагора.

 

 

Примеры решения задач на расчет электрических полей на основе принципа суперпозиции

Пример 3.1

Найти напряженность электрического поля в точках А и В
(см. рис.), лежащих на серединном перпендикуляре между точечными зарядами q₁ = 8 нКл и q₂ = –6 нКл, находящимися в вакууме. Расстояние между зарядами r = 10 см, АВ = 4 см, e = 1.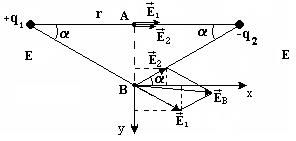

Дано:

q₁ = 8 нКл;

q₂ = -6 нКл;

r = 10 см;

AB = 4 см;

e = 1

Е_А - ?

Е_В - ?

Анализ и решение:

На рисунке показано расположение зарядов и точек А и В, для которых надо найти напряженность поля, и показан выбор системы координат.

а) В точке А поле создается двумя точечными зарядами q₁ и q₂. По определению напряженность поля - это сила с которой заряд, создающий поле, действует на единичный положительный точечный заряд, помещенный в точку А, поэтому вектора напряженносте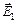й и 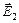в этой точке направлены в одну сторону. Суммарная напряженность находится как сумма напряжённостей полей отдельных зарядов

,

или в проекции на ось ОХ

.

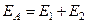Запишем формулы для вычисления модулей векторов напряженностей поля точечных зарядов q₁ и q₂ в точке А:

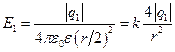и .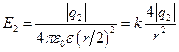

Для точки А получаем:

.

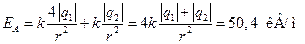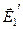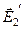б). В точке В векторы и направлены под углом 2a друг к другу и модули этих векторов не одинаковые, т.к. величины зарядов q₁ и q₂ разные.

Запишем формулы для вычисления модулей векторов напряженностей поля точечных зарядов q₁ и q₂ в точке В:

и .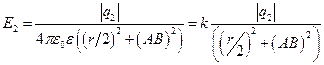

Каждый из этих векторов дает проекцию на обе координатные оси:

, , , .

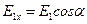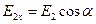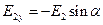Проекции суммарного вектора напряженности в точке В будут равны:

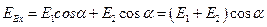и .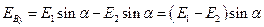

Теперь по теореме Пифагора можно получить формулу для вычисления модуля вектора напряженности электрического поля, создаваемого в точке В зарядами q₁ и q₂. .

С учетом всех полученных выражений, проделав алгебраические преобразования, получим окончательное выражение для вычисления искомой величины:

.

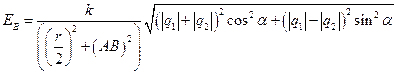Вычислим численное значение напряженности суммарного поля в точке В:

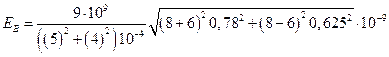
Окончательно получаем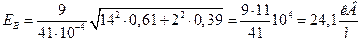

.

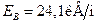Примечание. В некоторых случаях, когда решение связано с достаточно громоздкими алгебраическими преобразованиями, можно проводить расчеты по ходу решения задачи. Так можно было поступить и при решении этой задачи.

Ответ: напряженность электрического поля в точке А равна
Е_А = 50.4 кВ/м и направлена от заряда q₁ к заряду q₂. В точке В напряженность равна Е_В = 24,1 кВ/м и ее направление показано на рисунке.

Пример 3.1 Две длинные одноимённо заряженные нити расположены на расстоянии r₁= 10см друг от друга. Линейные плотности зарядов одинаковы и равны 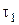= =10мкКл/м.

Найти модуль и направление напряжённости результирующего поля в точке А, удалённой от каждой нити на расстояние а = 10см.

 

Анализ :

Дано:
r	=10см =20см =10мкКл/м
r2
=
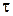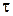
a	=10см
1) E-? 2) A-?

Электростатические поля, создаваемые различными распределениями зарядов, по принципу суперпозиции складываются в каждой точке пространства. Учитывая симметрию задачи, сделаем рисунок, расположив нити перпендикулярно плоскости чертежа. Точка А удалена от обеих нитей на расстояние а=r₁.Получили равносторонний треугольник. Для того, чтобы найти направление вектора напряжённости поля, создаваемого в точке А зарядом каждой нити, поместим в эту точку пробный заряд «+1» и определим, как поля нитей действуют на этот заряд. 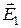Так как нити заряжены положительно, то они будут отталкивать пробный заряд и вектора и 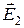будут направлены так, как показано на рисунке. Вектор напряжённости суммарного поля, согласно принципу суперпозиции, находится по правилу параллелограмма.

Сила взаимодействия этих заряженных нитей зависит от расстояния между ними, поэтому работу сил электростатического поля при раздвижении нитей надо вычислять через интеграл.

Решение:

1) Из рисунка видно, что 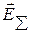направлен вправо, и модуль его можно найти как:

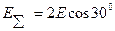
т.к. 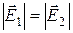и 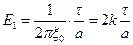, где k= .

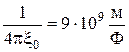Окончательно получаем

.

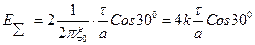
2) Сила взаимодействия заряженных нитей зависит от расстояния между ними. Каждая нить создаёт поле, и это поле действует на заряд другой нити. 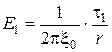- напряженность поля первой нити.

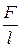-сила, действующая на единицу длины второй нити равна:

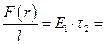
Работу этой силы можно вычислить как:

.

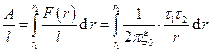Возьмём интеграл от этой функции. Все постоянные величины выносим за знак интеграла и получаем табличный интеграл, который равняется натуральному логарифму аргумента.

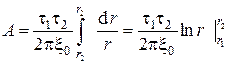
Подставим пределы интегрирования и окончательно получаем:

.

Используя данные задачи, получим численный ответ

 

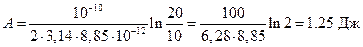
Ответ: 1) 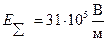2)

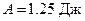
Пример 3.2

Положительный заряд q = 5 × 10^-8 Кл равномерно распределен по тонкому проволочному полукольцу радиуса R= 20 см. Определить напряженность поля Е в центре полукольца.

Дано:

q = 5 × 10^-8 Кл;

R = 20 см;

e = 1

Е –?

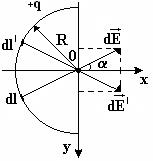Анализ и решение: В этой задаче поле создается зарядом q, распределенным по тонкому полукольцу радиуса R. Линейная плотность заряда равна: . Для такого случая нельзя непосредственно воспользоваться формулой напряженности для поля точечного заряда или бесконечной заряженной нити. Такую задачу можно решить, используя принцип суперпозиции. Разделим весь проводник на очень маленькие участки длиной dl, на каждый из которых приходится заряд dq =t × dl. Такой заряд можно считать точечным и величину напряженности поля этого заряда рассчитать по формуле

.

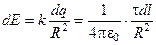На рисунке показан выбор осей координат и вектор напряженности поля 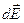, создаваемый в точке О зарядом 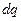.Учитывая симметрию задачи, удобно начало отсчёта системы координат связать с точкой О, центром полукольца, и направить оси координат так, как изображено на рисунке.

Спроектируем вектор 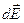на оси координат:

dЕ_x = dE × cosa;

dE_y = dE × sina.

Из симметрии видно, что каждому элементарному заряду dq найдется симметрично расположенный относительно оси ОХ заряд dq¢. Проекции напряженностей полей этих зарядов на ось ОУ дадут ноль при любых углах a.

Таким образом, надо найти только проекцию суммарного вектора на ось ОХ. Понятно, что в случае непрерывного распределения заряда суммирование следует заменить интегрированием по всей длине проволоки, на которой расположен заряд.

.

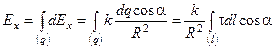В подынтегральное выражение входят две переменные l и a. Учитывая, что 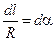и dl = Rda, заменим переменную интегрирования и получим

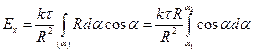
или

.

Из рисунка видно, что , а .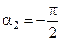

Окончательно получаем

;

; .

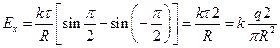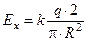Ответ: напряженность поля в центре кольца равна 7,2 кВ/м.

Пример 3.3

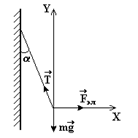
На рисунке изображены заряженная бесконечная плоскость с поверхностной плоскостью заряда s = 40 мкКл/ м² и одноименно заряженный шарик с массой m = l г и зарядом q = 1 нКл. Какой угол a с плоскостью образует нить, на которой висит шарик?

Дано:

s=40 мкКл/м²;

m = l r;

q = 1 нКл

a - ?

Решение:

Заряд находится в поле плоскости. На шарик действуют три силы, изображенные на рисунке. Запишем условие равновесия шарика: .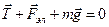

Спроектируем полученное уравнение на оси координат:

Ох: F_эл - T sina = 0;

Oy: T cosa - mg = 0.

Решая систему уравнений, получаем F_эл. = mg × tga_..

С другой стороны, F_эл. = qE, где Е - напряженность электрического поля, созданного бесконечной плоскостью.

Из полученной системы уравнений имеем

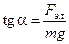, или .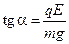

Поле бесконечной плоскости можно выразить следующим образом:

.

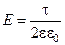В нашем случае заряд и плоскость находятся в воздухе, т.е. e = 1.

Окончательно запишем

.

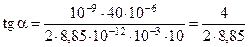tga = 0,2259 » 0,226

Ответ: нить составляет с плоскостью угол a = 13⁰.