Физический смысл производной

ГЛАВА 4

ПРОИЗВОДНАЯ И ДИФФЕРЕНЦИАЛ ФУНКЦИИ

Раздел математики, в котором изучается понятие производной и дифференциала функции, а также способы их применения к исследованию функций, называют дифференциальным исчислением.

 

Определение производной

К понятию производной приходят при изучении скорости изменения функции.

Пусть функция 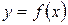определена и непрерывна на некотором интервале .

Проведем следующие операции:

− аргументу дадим приращение , такое что ;

− найдем соответствующее приращение функции:

;

− составим отношение:

;

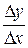− найдем предел этого отношения при :

.

Если этот предел существует, то его называют производной функции 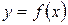и обозначают одним из символов: , , , , .

 

Определение.

Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

 

Записывают:

или .

Производная функции есть некоторая функция , произведенная из данной функции.

 

Определение.

Операция нахождения производной функции называется дифференцированием.

 

Определение.

Функция, имеющая производную в каждой точке интервала , называется дифференцируемой на этом интервале.

 

Примеры

1. Найти производную функции .

1) ;

 

2)

;

 

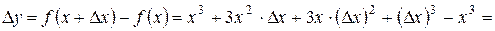
3) ;

 

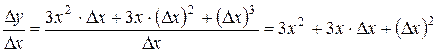4) ;

.

 

2. Найти производную функции .

1) ;

 

2)

;

 

3) ;

;

.

 

Геометрический смысл производной

Рассмотрим график функции , непрерывной на интервале (рис.4.1). На кривой выберем произвольную точку . Если аргументу х дать приращение , то на графике новому значению аргумента будет соответствовать точка . Проведем через точки М и секущую и пусть φ − угол, который секущая М образует с остью Ох.

 

Рис. 4.1

 

Из получаем

.

Пусть , тогда точка , а секущая М будет стремиться занять положение касательной МТ, проходящей через точку М.

 

Определение.

Касательной к кривой в точке М называется прямая МТ, являющаяся предельным положением секущей М , при стремлении точки к точке М по кривой (или при ).

 

Значит, при , где − угол наклона касательной МТ к оси Ох. Тогда

.

Следовательно,

.

Таким образом, геометрический смысл производной состоит в том, что значение производной равно тангенсу угла, образованного касательной к графику функции в соответствующей точке, с положительным направлением оси Ох.

Отметим, что понятие производной дает возможность написать уравнение касательной к графику функции.

Уравнение касательной − это уравнение прямой, проходящей через заданную точку: , угловой коэффициент которой равен .

Следовательно, уравнение касательной будет

или

.

 

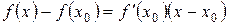Если касательную к кривой в некоторой точке провести невозможно, то это означает, что функция недифферинцируема в этой точке.

 

Физический смысл производной

Рассмотрим функцию, аргументом которой является время t. Если функция − пройденный путь , тогда отношение

представляет собой среднюю скорость движения за промежуток времени . Предел этого отношения (производная по определению)

есть скорость движения в момент времени t или мгновенная скорость движения.

В общем случае, если функция описывает какой-либо физический процесс, то отношение

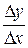− средняя скорость изменения у относительно х,

− мгновенная скорость изменения у.

Таким образом, производная есть скорость протекания процесса.

 

4.4. Зависимость между непрерывностью
и дифференцируемостью функции

Сформулируем необходимое условие существования производной.

 

Теорема.

Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна.

 

Заметим, что обратное утверждение неверно: непрерывная функция может не иметь производной.

Например, функция непрерывна при , но не дифференцируема для этого значения, так как в точке графика функции не существует касательной.

Таким образом, непрерывность функции необходимое, но не достаточное условие дифференцируемости функции.