Устойчивость стержней переменного сечения по длине и составных стержней

Стержни переменного поперечного сечения по длине приме­няются с целью уменьшения массы конструкции. Примером могут служить крановые стрелы. Гибкость стержня зависит от закона изменения момента инерции поперечного сечения по его длине. На рис. 79 показан шарнирно опертый по концам стержень, для каждой половины которого момент инерции изменяется по сте­пенному закону

J = J₂(х/b)^m, (249)

где J₂– момент инерции стержня в среднем сечении.

Рисунок 79 – Схема нагружения стержня с переменным моментом инерции сечения по длине

Важным является случай изменения момента инерции стержня по квадратич­ному закону. Это характерно для решет­чатых стержней с поясами постоянного поперечного сечения при изменении ши­рины h (рис. 79) их по линейному за­кону. Если стержень состоит из двух поя­сов постоянного сечения F_п, то J = 2 [J_с + F_п (h/2)²]≈ 2F_п (h/2)². Собственный момент инерции сечения пояса (ветви) обычно мал по сравнению с F_п h²/4и им можно пренебречь. Тогда момент инерции J вдоль стержня изме­няется по квадратичному закону [см. фор­мулу (249)]. Расстояние между поя­сами (рис. 79) h равно h = h₂x/b. Диф­ференциальное уравнение упругой линии используем в виде

EJ₂ (x / b)^m (d²y/dx²) + Py = 0. (250)

Граничные условия:

при х = b dy/dx = 0; при х = b – l/2= b₁ у = 0. (251)

Формулу критической силы таких стержней можно пред­ ставить в виде, аналогичном формуле Эйлера для стержней постоянного поперечного сечения по длине

Р_КР = π² EJ₂ / (μl)², (252)

где μ – коэффициент приведения расчетной длины, μ = 1 / .

При расчете на устойчивость стержня переменного сечения принимают, что он имеет постоянное значение момента инерции J = J₂, равное значению наибольшего момента инерции стержня переменного сечения при проверке устойчивости в данной плоскости.

Коэффициент приведения μ длины стержня зависит от двух коэффициентов

μ = f (μ₁ μ₂), (253)

где μ₁ – см. в формуле (242); μ₂ – коэффициент, учитывающий закон изменения моментов инерции по длине стержня.

Устойчивость составных центрально-сжатых стержней (рис. 80) зависит от жесткости ветвей и жесткости соединяющих их решеток или планок. Из теории изгиба балок известно, что влияние поперечной силы в случае сплошного сечения мало. Однако для составных стержней ее надо принимать во вниманиеиз-за возникающих деформаций соединительных планок и решеток

Критическая нагрузка

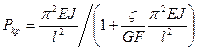. (254)

Значение 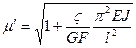(255)

является коэффициентом приведения длины стержня.

Рисунок 80 – Схемы для расчета устойчивости составного стержня: а – деформация стержня при продольном изгибе; б – составные стержни, ветви которых соединены решеткой и планками; в, г – сечения составных стержней из двух и четырех ветвей соответственно.

Рассмотрим составной стержень из двух ветвей, соединенных решеткой (рис. 80, б, в).Расстояние между центрами тяжести сечения ветвей h,длина отсека а,длина диагонали d (рис. 81). Момент инерции сечения приближенно равен

J ≈ F_пh²/2≈ Fh²/4, (256)

где F_п – площадь сечения ветви (пояса); F – полная площадь сечения.

Средняя по сечению стержня деформация сдвига γ связана с поперечной силой соотношением

γ = ςQ /(GF) (257)

отсюда ς /(GF) = γ /Q подставляется в (254) и (255).

Значение γ/Q отвечает тому или иному типу соединительной решетки. На рис.81 показано изменение геометрии стенок стержня при деформации диагонали (раскоса). Усилие в раскосе N_р = Qd/h. (258)

Удлинение его равно Δd = Qd²/(EF_ph), (259)

где F_p – площадь сечения раскоса.

Угол сдвига γ равен γ = δ/а = Δd/(а sin α) = Δd ∙ d /(ah). (260)

Отсюда γ/Q = d³/(EF_p аh²). (261)

Подставив эту величину вместо х /(GF)в формулы (254) и (250), получим:

; (262)

, (263)

где λ_z – гибкость стержня относительно свободной оси z,λ_z = l/r = l .

Приведенная гибкость для стержня из двух ветвей с решет­ками

λ_пр = μ' λ_z = . (264)

Для стержня из четырех ветвей с решетками (рис. 80, г)

λ_пр = , (265)

где F – площадь сечения всего стержня; λ_ст – наибольшая гибкость всего стержня; F_P1 и F_P2 – площади сечения раскосов решеток, лежащих в плоскостях возможной потери устойчивости; k₁и k₂– коэффициенты, зависящие от углов между раскосом и ветвью α₁и α₂, k = 45; k = 31; k = 27 при α= 30°; α= 40°; а = 45÷60° соответственно.

Для составных стержней из двух ветвей с планками в двух плоскостях (см.рис.80,в)

λ_пр = 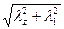. (266)

а с планками в четырех плоскостях

λ_пр = 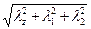. (267)

где λ₁, λ₂ – гибкости отдельных ветвей относительно собствен­ных осей 1-1; 2-2, параллельных главным осям инерции состав­ного стержня на участках между приваренными планками (в свету); λ₁ и λ₂ должны иметь значение не более 40 для стальных кон­струкций и не более 30 – для конструкций из алюминиевых сплавов. Составные элементы из уголков и т. п., соединенные непосредственно друг с другом или через прокладки, рассчиты­ваются как сплошностенчатые. При этом расстояния между их соединениями (прокладками и т. п.) не должны превышать 40r для сжатых элементов и 80r для растянутых элементов (r – ра­диус инерции элемента относительно оси, параллельной пло­скости прокладок).

Планки как соединительные элементы центрально-сжатых составных стержней рассчитываются на действие поперечной силы. Последняя возникает при изгибе стержней в момент потери устой­чивости. При расчете планок исходят из значения условной по­перечной силы Q_усл (Н), принимаемой равной 200F для конструк­ций из углеродистых сталей и 400F – из низколегированных, где F (см²) – площадь брутто всего сечения стержня.

При расчете планок и их соединений с ветвями составной стержень рассматривается как сжатая безраскосная ферма с же­сткими узлами и нулевыми точками в середине панелей и планок. На рис.82 показана часть фермы в равновесии. Обозначив через с - расстояние между осями ветвей, через Т = Ql₁/c – силу, срезывающую планку, получим изгибающий момент, действу­ющий на планку и ее соединение,

М = Тс/2= Ql₁/2, (268)

где Q = Q_усл. По значениям М и Т производится расчет планок и их соеди­нений.