Системы отсчета в космической съемке

Ориентация космических снимков в пространстве выполняется при помощи звездной камеры путем фотографирования звездного неба. Таким образом, для координатно-временной привязки к местности необходимо учитывать орбитальное движение космического аппарата и, следовательно, использовать системы координат, в которых удобно описывать орбитальное движение.

Рисунок 1 — Инерциальная геоцентрическая система координат

Инерциальная система координат. В качестве инерциальной системы координат при изучении движения ИСЗ используют экваториальную геоцентрическую систему координат (рисунок 1.1), начало O которой находится в центре масс земли, ось Ox направлена в точку весеннего равноденствия g, ось Oz совпадает с осью вращения Земли и положительна в направлении к Северному полюсу, а ось Oy дополняет систему до триэдра правой ориентации.

Ось вращения Земли совершает очень медленное движение по круговому конусу — прецессию, и одновременно — небольшие колебания, при которых изменяется угол между осью вращения тела и осью, вокруг которой происходит прецессия, — нутацию. Поэтому экваториальная система координат непрерывно медленно изменяется сложным образом вследствие прецессии и нутации. Для того чтобы экваториальная система стала инерциальной, ее необходимо зафиксировать относительно некоторого времени (эпохи) Т₀. В космических исследованиях в качестве стандартной эпохи принимается эпоха Т₀ = 2000,0.

Поскольку нутационные эффекты не превосходят 10^–4, при учете нутации можно ограничиться только линейными членами при разложении элементов матрицы нутации в ряды Тэйлора.

Положение точки i пространства в инерциальной системе координат задается ее геоцентрическим радиус-вектором , прямым восхождением a_i и склонением d_i.

Прямое восхождение a_i отсчитывается в плоскости экватора против часовой стрелки от точки весеннего равноденствия до проекции радиус-вектора и обычно задается в часовой мере. Склонение d_i представляет собой угол между геоцентрическим радиус-вектором и плоскостью экватора.

Таким образом, инерциальные геоцентрические координаты x, y, z задаются формулами:

(1.1)

а обратное преобразование

(1.2)

.

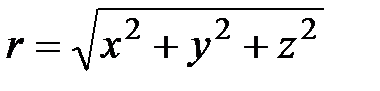Инерциальная система координат устанавливается с помощью каталогов координат звезд.

Гринвичская система координат. Инерциальная система координат не всегда удобна, так как помимо трех координат точки необходимо указывать и момент времени, в который точка имеет заданные координаты. Поэтому применяют геоцентрическую гринвичскую систему координат OXYZ, начало которой, так же как и инерциальной, совпадает с центром масс Земли, ось OZ направлена в средний Северный полюс Земли 1900–1905 г.г., а ось OX лежит в плоскости экватора 1900–1905 г.г. и направлена в точку пересечения экватора и меридиана Гринвича этой эпохи.

Переход от истинных инерциальных координат на эпоху фотографирования t_i к гринвичским координатам выполняют в два этапа.

На первом этапе система инерциальных истинных координат поворачивается вокруг оси OZ на угол, численно равный истинному звездному времени S в Гринвиче, после чего ось OX совпадет с мгновенным меридианом Гринвича:

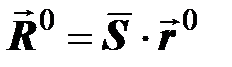, (1.3)

где 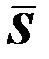– ортогональная матрица вращения, соответствующая повороту на угол S, численно равный звездному времени в Гринвиче, то есть

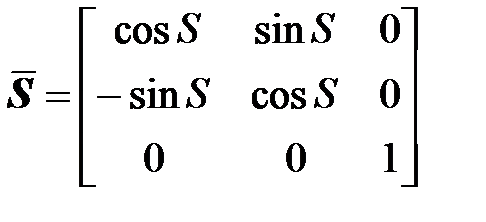, (1.4)

где S определяется по формулам

(1.5)

где 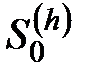– истинное звездное время, значения которого публикуются в Астрономическом ежегоднике в разделе «Звездное время», ч (в часах);

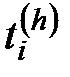– всемирное время в момент фотографирования, ч (в часах);

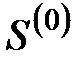– звездное время в градусах.

На втором этапе перехода ось OZ должна быть направлена в средний полюс эпохи 1900–1905 гг. Для этого необходимо располагать истинными координатами полюса 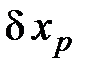и 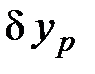на эпоху фотографирования t_i относительно среднего полюса 1900–1905 г.г., которые публикуются в специальном издании Международной службы движения полюсов (МСДП).

Вводят 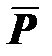— матрицу, описывающую движение полюса,

. (1.6)

Координаты полюса в матрице (1.6) должны быть выражены в радианах. При вычислениях используют матрицу :

. (1.7)

Следовательно, переход от направления на звезду, заданного в средней инерциальной системе координат на эпоху каталога Т₀, к гринвичской системе координат выполняют на основании соотношения

. (1.8)

Геодезические системы координат. В геодезии и фотограмметрии наиболее широкое применение получили геодезические системы координат, заданные относительно референц-эллипсоидов. Международный астрономический союз (МАС) в 1976 г. рекомендовал общий земной эллипсоид с параметрами:

большая полуось a_e = 6378140 м;

сжатие a_e = 1/298,57;

квадрат эксцентриситета ;

квадрат второго эксцентриситета ;

параметр ;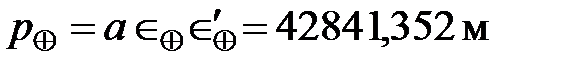

параметр .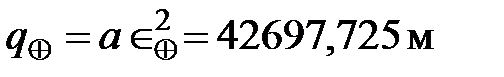

Геодезическую систему координат задают широтой B₀, долготой L₀ и высотой H₀ исходного пункта и параметрами референц-эллипсоида a_e и a_e.

Начало геодезической системы координат O_Г, как правило, не совпадает с центром масс Земли на некоторую величину 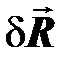, однако всякая геодезическая прямоугольная система практически параллельна гринвичской системе координат.

Геодезические координаты задают в виде прямоугольных координат X_Г, Y_Г, Z_Г или в форме криволинейных координат B, L, H (геодезические широта, долгота и высота, отсчитываемая вдоль нормали N к поверхности эллипсоида). Ось O_ГX_Г направлена в точку пересечения геодезического меридиана Гринвича с плоскостью экватора, а ось O_ГZ_Г совпадает с осью вращения эллипсоида. Ось O_ГY_Г дополняет систему до триадра правой ориентации и положительна к востоку.

Связь прямоугольных и криволинейных геодезических координат:

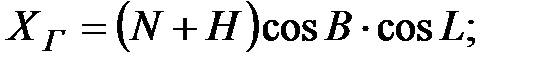
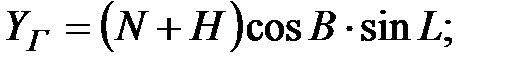(1.9)

,

где N — нормаль к поверхности эллипсоида,

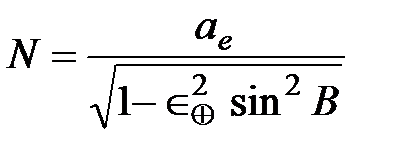, (1.10)

где Î_Å — эксцентриситет земного эллипсоида.

Обратный переход от прямоугольных координат к криволинейным сложнее, поскольку требует последовательных приближений при вычислении широты.

Для таких вычислений Боурингом был предложен следующий алгоритм расчета, который обеспечивает необходимую точность.

Сначала вычисляют вспомогательный угол j:

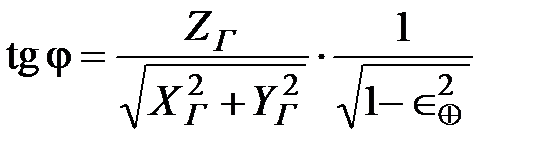. (1.11)

Затем широту B определяют по формуле:

, (1.12)

где — второй эксцентриситет земного эллипсоида,

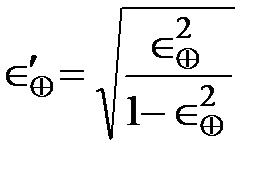. (1.13)

Геодезическую долготу L определяют по формуле:

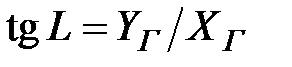, (1.14)

а высоту H — на основании равенств:

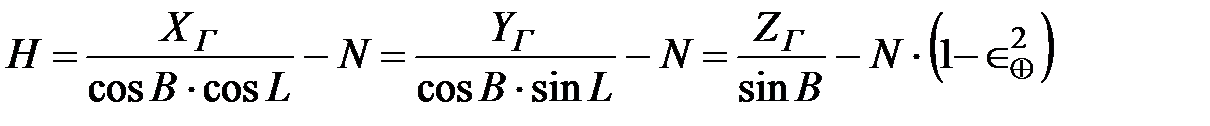. (1.15)