Приложения частных производных

5.2.1.Для функции в точке 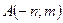найти градиент и производную по направлению .

5.2.2. Найти наибольшее и наименьшее значения функции

z = 4x² + y² – 4mx – 2ny + m² + n² в области заданной неравенствами:

x ≥ 0; nx – my 0; x+ y – m – n 0

 

Двойные, тройные и криволинейные интегралы.

 

Двойные интегралы.

6.1.1.Изменить порядок интегрирования:

.

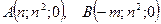6.1.2.Сделать чертеж и найти объем тела, ограниченного поверхностями и плоскостью, проходящей через точки и .

6.1.3.Сделать чертеж и найти площадь фигуры, ограниченной линиями:

а) .

Тройные интегралы.

6.2.1.Найти , если тело V ограниченно плоскостям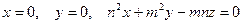и и .

6.2.2.Найти объем тела, ограниченного поверхностями .

Криволинейные интегралы.

6.3.1.Вычислить , где , , а контур С образован линиями , : а) непосредственно; б) по формуле Грина.

6.3.2.Вычислить 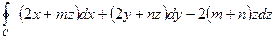, где контур С является одним витком винтовой линии:

.

 

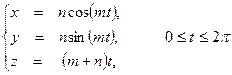Элементы теории поля.

Дифференциальные операции.

7.1.1.В точке 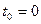составить уравнение касательной прямой и нормальной плоскости к кривой

 

.

 

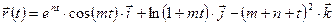7.1.2.Найти в точке градиент скалярного поля

.

7.1.3.Найти в точке дивергенцию векторного поля

.

7.1.4.Найти в точке ротор векторного поля

.

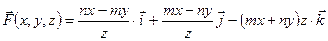Интегралы и интегральные теоремы.

7.2.1.Убедиться, что поле потенциально, и найти его потенциал.

7.2.2.Даны поле и цилиндр D, ограниченный поверхностями z=0, z=m, x²+y²=(n+1)². Найти:

а) поток поля через боковую поверхность цилиндра в направлении внешней нормали;

б) поток поля через всю поверхность цилиндра в направлении внешней нормали непосредственно и с помощью теоремы Остроградского – Гаусса.

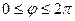7.2.3.Даны поле и замкнутый виток , ( обход контура происходит в направлении, соответствующем возрастанию параметра φ). Найти циркуляцию поля вдоль контура γ непосредственно и с помощью теоремы Стокса.

 

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

 

Уравнения первого порядка.

8.1.1.Найти общее решение уравнения:

а) 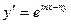; в) .

8.1.2.Скорость роста банковского вклада пропорциональна с коэффициентом равным величине вклада. Найти закон изменения величины вклада со временем, если первоначальная сумма вклада составляла миллионов рублей.

Линейные уравнения высших порядков.

8.2.1.Решить задачу Коши:

а)

б)

Системы линейных уравнений.

8.3.1.Решить систему линейных уравнений

с начальными условиями .

9. Ряды.

Числовые ряды.

9.1.1.Исследовать на сходимость ряды с положительными членами:

а) ; б) ;

в) ; г) .

9.1.2.Исследовать на условную сходимость и абсолютную сходимость знакочередующиеся ряды:

а) 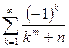; б) .

Степенные ряды.

9.2.1.Найти область сходимости степенного ряда:

а) ; б) .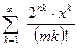

9.2.2.Разложить функцию 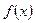в ряд Тейлора в окрестности точки х₀:

а) ; б) .

9.2.3.С помощью разложения в ряд вычислить приближенно с точностью 0,001 значения:

а) ; б) .

Ряды Фурье.

9.3.1.Разложить функцию 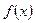в ряд Фурье в указанном интервале:

а)

в интервале ;

б) в интервале .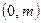

в) в интервале .