 |
Главная |
Функции комплексного переменного
|
из
5.00
|
Действия с комплексными числами.
10.1.1.Выполнить действия:
а) 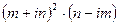 ; б)
; б) 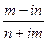 .
.
10.1.2.Решить уравнения:
а) 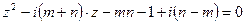 ; б)
; б) 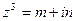 .
.
Аналитические функции.
10.2.1.Показать, что функция 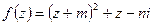 аналитична.
аналитична.
10.2.2.Известна вещественная часть u(x,y)=m(x2-y2)+mx-ny аналитической функции f(z), (z=x+iy). Найти функцию f(z).
Интегрирование функций комплексного переменного.
10.3.1.Вычислить 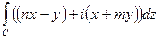 , где контур С – незамкнутая ломанная, соединяющая точки
, где контур С – незамкнутая ломанная, соединяющая точки 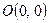 ,
, 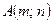 и
и 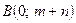 .
.
10.3.2.Вычислить с помощью интегральной формулы Коши
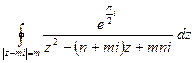 .
.
Ряды Тейлора и Лорана.
10.4.1.Разложить функцию 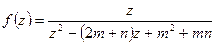 в окрестности точки
в окрестности точки 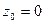 в ряд Тейлора и найти радиус сходимости ряда.
в ряд Тейлора и найти радиус сходимости ряда.
10.4.2.Разложить функцию 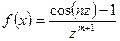 в окрестности точки
в окрестности точки 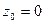 в ряд Лорана.
в ряд Лорана.
10.4.3.Разложить функцию 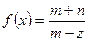 в ряд Лорана по степеням
в ряд Лорана по степеням 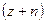 и найти область сходимости ряда.
и найти область сходимости ряда.
Вычеты и их приложения.
10.5.1.Определить тип особых точек функции 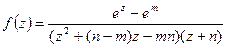 и найти вычеты в конечных особых точках.
и найти вычеты в конечных особых точках.
10.5.2.Вычислить с помощью вычетов 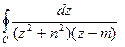 , где контур C, заданный уравнением
, где контур C, заданный уравнением 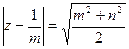 , обходится против часовой стрелки.
, обходится против часовой стрелки.
Операционное исчисление.
Нахождение изображений и восстановление оригиналов.
11.1.1.Найти изображения функций:
а) 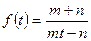 ; б)
; б) 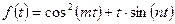 .
.
11.1.2.Восстановить оригиналы по изображениям:
а) 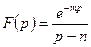 ; б)
; б) 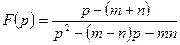 .
.
Приложения операционного исчисления.
11.2.1.Решить операционным методом дифференциальное уравнение:
а) 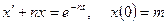 ;
;
б) 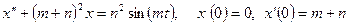 .
.
Теория вероятностей.
Случайные события.
12.1.1.В коробке находятся m+2 синих, n+3 красных и 2n+1 зеленых карандашей. Одновременно вынимают m+3n+2 карандашей. Найти вероятность того, что среди них будет m+1 синих и n+1 красных.
12.1.2.В первой урне находятся m+2 шаров белого и n шаров черного цвета, во второй — m+n белого и m синего, в третьей — n+3 белого и m+1 красного цвета. Из первой и второй урны наудачу извлекают по одному шару и кладут в третью. После этого из третьей вынимают один шар. Найти вероятность того, что он окажется белым.
12.1.3.Вероятность попадания стрелка в мишень при одном выстреле равна 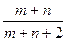 . Производится n+4 выстрела. Найти вероятность того, что он промахнется не более двух раз.
. Производится n+4 выстрела. Найти вероятность того, что он промахнется не более двух раз.
12.1.4.Каждый избиратель независимо от остальных избирателей, отдаёт свой голос за кандидата А с вероятностью 0,1(m + n) и за кандидата В – с вероятностью 1–0,1(m + n). Оценить вероятность того, что в результате голосования на избирательном участке (5000 избирателей) один из кандидатов опередит другого:
а) ровно на 1900 голосов;
б) не менее, чем на 1900 голосов.
Случайные величины.
12.2.1.Случайная величина Х равна числу появлений «герба» в серии из n+3 бросаний монеты. Найти закон распределения и функцию распределения F(x) этой случайной величины; вычислить ее математическое ожидание MXи дисперсию DX; построить график F(x).
12.2.2.Закон распределения дискретной случайной величины X имеет вид:
| xi | -2 | -1 | m | m+n | |
| pi | 0,2 | 0,1 | 0,2 | p4 | p5 |
Найти вероятности p4, p5, и дисперсию DX, если математическое ожидание MX=-0,5+0,5m+0,1n.
12.2.3.Плотность распределения непрерывной случайной величины X имеет вид:
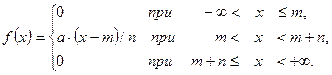
Найти:
а) параметр а; б) функцию распределения 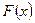 ;
;
в) вероятность попадания случайной величины X в интервал
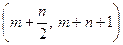 ;
;
г) математическое ожидание MX и дисперсию DX.
Построить график функций 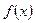 и
и 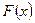 .
.
12.2.4.Случайные величины 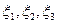 имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания Mξi=m+n, а дисперсия Dξ1=n2/3. Найти вероятности: а)
имеют равномерное, пуассоновское и показательное распределения соответственно. Известно, что математические ожидания Mξi=m+n, а дисперсия Dξ1=n2/3. Найти вероятности: а) 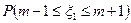 ; б)
; б) 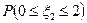 ; в)
; в) 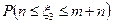 .
.
|
из
5.00
|
Обсуждение в статье: Функции комплексного переменного |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

