Виды сопряжений. Коробовые кривые

СОПРЯЖЕНИЯ

Плавный переход одной линии в другую называется сопряжением.

Сопряжение прямого угла. Пусть необходимо выполнить сопряжение прямого угла радиусом сопряжения, равным отрезку АВ (R=AB). Найдем точки сопряжения. Для этого поставим ножку циркуля в вершину угла и раствором циркуля, равным отрезку АВ, сделаем засечки на сторонах угла. Полученные точки а и b являются точками сопряжения. Найдем центр сопряжения — точку, равноудаленную от сторон угла. Раствором циркуля, равным радиусу сопряжения, из точек а и b проведем внутри угла две дуги до пересечения друг с другом. Полученная точка О — центр сопряжения. Из центра сопряжения описываем дугу заданного радиуса от точки а до точки Ь. Обводим вначале дугу, а затем прямые линии (рис. 70).

Сопряжение острого и тупого углов.

Чтобы построить сопряжение острого угла, возьмем раствор циркуля, равный заданному радиусу R=AB. Поочередно поставим ножку циркуля в двепроизвольные точки на каждой из сторон острого углса. Проведем четыре дуги внутри угла, жак показано на ргас. 71, а. К ним проведем две касательные до пересечения в точке О — центре сопряжения (рис. 71, б)- Из центра сопряжения опустим перпендикуляры на стороны угла. Полученные точки а и b будут точками сопряжения (рис. 71, б). Поставив ножку циркуля в центр сопряжения (О), раствором циркуля, равным заданному радиусу сопряжения (R=AB), проведем дугу сопряжения. Аналогично построению сопряжения острого угла строят сопряжение (скругление) тупого угла.

Сопряжение двух параллельных прямых.

Заданы две параллельные прямые и точка d, лежащая на одной из них (рис.72). Рассмотрим последовательность построения сопряжения двух прямых. В точке d восставим перпендикуляр до пересечения его с другой прямой. Точки d и е являются точками сопряжения. Разделив отрезок de пополам, найдем центр сопряжения. Из него радиусом сопряжения проводим дугу, сопрягающую прямые.

Сопряжение дуг двух окружностей дугой заданного радиуса.
Существует несколько типов сопряжения дуг двух окружностей дугой заданного радиуса: внешнее, внутреннее и смешанное.

Рассмотрим пример внешнего сопряжения дуг двух окружностей дугой заданного радиуса. Заданы радиусы Rx и R2 дуг двух окружностей (длины радиусов показаны отрезками прямых). Необходимо построить их сопряжение третьей дугой радиуса R (рис. 73, а). Для нахождения центра сопряжения проводим две вспомогательные дуги: одну радиусом ОхО = Ri + R, а другую 020 = R2 + R. Точка пересечения вспомогательных дуг является центром сопряжения. Точки сопряжения К лежат в пересечении прямых dO и 020 с дугами заданных окружностей. Из центра сопряжения радиусом сопряжения проводим дугу, соединяя точки сопряжений. При обводке построений вначале изображают дугу сопряжения, а затем дуги сопрягаемых окружностей (рис. 73, б). Внутреннее сопряжение дуг двух окружностей дугой заданного радиуса.

При внутреннем сопряжении сопрягаемые дуги окружностей находятся внутри дуги сопряжения (рис. 74).
Даны две дуги окружностей с центром d и 02, радиусы которых соответственно равны Rx и R2. Необходимо построить сопряжение этих дуг третьей дугой радиуса R. Находим центр сопряжения. Для этого из центра d радиусом, равным R—Rb и из центра 02 радиусом, равным R—R2, описывают вспомогательные дуги до их взаимного пересечения в точке О. Точка О будет центром сопрягающей дуги радиуса R. Точки сопряжения К лежат на линиях ООх и 002, соединяющих центры дуг окружностей с центром сопряжения.

Коробовые кривые.

Коробовые кривые - это кривые, составленные из дуг разных радиусов, описанных из нескольких центров. Ввиду того, что вычерчивание кривых по точкам представляет собой некоторое затруднение, на практике их заменяют коробовыми кривыми. Необходимое условие для плавности кривой состоит в том, чтобы смежные дуги в конечной точке имели общую касательную, или иначе, чтобы центры смежных дуг лежали на перпендикуляре к касательной, проведенной через точку сопряжения дуг.

Рисунок 1 Построение коробовой кривой.

Рассмотрим построение коробовой кривой по заданной ширине АВ и высоте ОС (Рисунок 1) при условии, что ОС должна быть меньше половины АВ. Проводим две взаимно перпендикулярные линии и на горизонтальной прямой от точки О откладываем АВ, а на перпендикуляре от точки О вверх откладываем ОС. Соединяем точку А с С прямой линией, а из центра О радиусом ОА проводим дугу до пересечения с ОС в точке D. Отрезок CDСА, получаем точку Е, а отрезок АЕ делим пополам и проводим серединный перпендикуляр к отрезку до пересечения его с прямой АВ в точке О2 и с прямой ОС в точке О1. Переносим точку О2 в точку О3, ей симметричную, и получаем три центра, из которых и проводим кривые АМ, MN и NB.переносим на прямую

Построение овала по заданным осям АВ и CD.

Овал - это тоже коробовая кривая, состоящая из двух конгруэнтных частей. Таким образом, построение овала сводится к построению двух симметричных коробовых кривых, как это было описано ранее, но в этом случае построение повторяют в нижней части осевой линии АВ следующим образом (Рисунок 2). Полученную точку О1 переносят в симметричную ей точку О4 и соединяют ее с точками О2 и О3, продолжая эти прямые с тем, чтобы проводимые дуги их пересеклись. Таким образом, получаем центры, из которых проводим дуги овала.

Рисунок 2 Построение овала.

Форма овала будет зависить от соотношения большой и малой осей: чем больше малая ось, тем круглее овал, и чем меньше малая ось, тем овал будет уже.

7. Лекальные кривые. Общие сведения.

Многие технические детали содержат кривые поверхности, которые на чертежах изображаются соответствующими кривыми линиями. Существует целая группа кривых линий, построить которые можно только по точкам при помощи лекал. Они называются лекальными.

Лекальные кривые бывают закономерные и незакономерные. Закономерными являются кривые, форма которых определяется уравнением. Незакономерными — кривые, форма которых может быть задана только графически.

Вычерчивание лекальной кривой начинают с построения принадлежащих ей точек. Необходимое их количество определяется длиной изображаемого участка и формой кривой. Построение точек практически может быть выполнено несколькими способами. Выбор способа также зависит от размеров изображений, длины участка кривой, его кривизны и других обстоятельств.

Лекала, с помощью которых затем обводят точки, имеют разную форму, т. е. кромки имеют различную кривизну на разных участках, хотя все участки плавно переходят один в другой. Подбирать лекала следует таким образом, чтобы их форма возможно больше соответствовала форме изображаемой кривой. Каждое лекало может быть использовано для обводки нескольких различных кривых. Однако некоторые из них специально предназначены для обводки эллипсов, другие для обводки парабол, третьи для обводки гипербол и т. п. .

Перед обводкой построенные точки необходимо соединить плавной тонкой линией карандашом от руки. Кривизну лекал желательно подбирать так, чтобы можно было соединить плавной кривой не меньше трех точек. Так, например, на рис. 86, а лекало совпадает с кривизной участка между первыми тремя точками 1, 2 и 3,но обводят участок кривой только между первыми двумя точками 1 и 2. Затем подбирают участок лекала, соединяющий следующие три или более точек, начиная от точки 2, и обводят очередной участок до предпоследней точки, На рис. 86, б кромка лекала совпадает с четырьмя точками 2,3,4 и 5, но обведена кривая только между точками 2, 3 и 4. Оставляя не обведённым каждый раз последний участок, добиваются плавной кривой. Обводят лекальную кривую слева направо, последовательно перемещая или меняя лекала в зависимости от кривизны последующих участков линии.

8. Эллипс. Конструктивные элементы. Способы построения. 8,9,10,

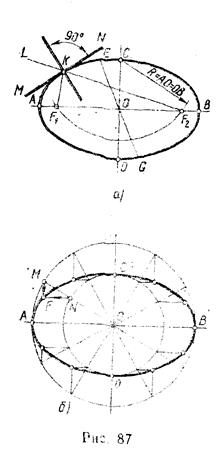Эллипс. Эллипсом называется плоская замкнутая кривая, сумма расстояний от любой точки которой до двух данных точек F1 и F2 – фокусов эллипса – величина постоянная, равная длине большой оси (рис. 87, а).

У эллипса различают две оси: большую ось (АВ) и малую ось (CD).
Фокусы эллипса располагаются на его большой оси (АВ) симметрично относительно точки О.
Расстояние между фокусами Fx и F2 называется фокальным.

Прямые FXKи F2K, соединяющие произвольную точку эллипса с его фокусами, называются радиус-векторами: Сумма радиус-векторов всегда равна длине большой оси эллипса, т. е. F1K-\-F2K=AB. Фокусы удалены от концов С и Dмалой оси эллипса на расстояние, равное половине его большой оси. Следовательно, зная размеры осей эллипса, всегда можно построить фокусы при помощи дуги радиуса R=AB/2=AO.

Рассмотрим пример построения эллипса по заданному расстоянию между фокусами F₁ и F и его большой оси АВ (Рисунок 2). Для этого откладываем от точек А иВ по половине расстояния между фокусами и получаем точки Е иЕ₁ (таким же образом можно использовать любую точку, взятую на АВ между фокусами). Через точку О перпендикулярно АВ проводим линию, на которой будет расположена малая ось эллипса СD. Для этого делаем засечки на этой прямой из точки F₁ или Fрадиусом, равным половине длины большой оси, и получаем малую ось эллипса CD.

Делим большую окружность на равные части (6 – 8/12) аналогично маленькую. Соединяем противоположные точки большой окружности через центр + соединяем точки малой окр по горизонтали. Опускаем перпендикуляры к проведенным горизонталям из точек большой окр, полученные точки соединяем с помощью лекала.

Способ дополнительных окружностей: Разделим большую окружность на произвольное количество частей, например, на 12 равных, как показано на рис. 76, а. Соединим точки деления с центром О, разделив таким образом окружность меньшего диаметра на такое же количество частей. Из точек, полученных при делении меньшей окружности (за исключением точек С и D), проводим горизонтальные линии, параллельные АВ (рис. 76, а). Из точек деления, полученных на большей окружности (за исключением точек 1, 4, 7, 10), проводим вертикальные линии, параллельные CD, до пересечения их с ранее проведенными горизонтальными прямыми (рис. 76, б). Таким образом мы получили ряд точек, принадлежащих эллипсу. Эллипсу также принадлежат точки А, В, С, D. Последовательно соединяя точки плавной кривой, получим изображение эллипса, которое обводится с помощью лекал (рис. 76, в).

Кривые, которые строятся с помощью лекал, называются лекальными кривыми.