 |
Главная |
Основные свойства операций над событиями
|
из
5.00
|
Литература
1. А.А. Боровков, Курс теории вероятностей, Москва, Наука, 1972.
2. Б.В. Гнеденко, Курс теории вероятностей, Москва, Наука, 1961.
3. Ю.В. Прохоров, Ю.А. Розанов, Теория вероятностей, Москва, Наука, 1987.
4. В.С. Вентцель, Теория вероятностей, Москва, Высшая школа, 1998.
5. И.Н. Коваленко, А.А. Филиппова. Курс теории вероятностей и математическая статистика, Москва, Высшая школа, 1982.
6. Коломиец Э.И., Дегтярев А.А. Сборник задач по теории вероятностей, Учебное пособие, 2006
План лекции
1.Случайный эксперимент, случайные события
2. Операции над событиями
3. Статистическое определение вероятности.
4. Классическое определение вероятности. Комбинаторные формулы.
5. Геометрические вероятности.
6. Свойства вероятности.
Т.В. изучает так называемые случайные события и устанавливает закономерности в проявлении таких событий.
Для введения понятия случайного события рассмотрим некоторые примеры реальных экспериментов.
1. Производится бросание монеты, результатом данного эксперимента могут быть два исхода; выпадение герба или решетки.
2. Из колоды 36 карт наудачу выбирают карту. Имеется 36 возможных исходов, которые можно закодировать числами 1,…,36.
3. Ставят на испытание n изделий. Через время Т испытание прекращают и фиксируют, какие изделия вышли из строя. Исходы эксперимента – n-мерные булевы векторы 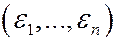 , где
, где 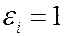 , если i-ое изделие вышло из строя и
, если i-ое изделие вышло из строя и 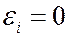 в противном случае.
в противном случае.
4. Ставят на испытание n изделий. Испытание во времени не ограничивают; для каждого i измеряют время ti отказа i-го изделия. Исходы эксперимента – n-мерные векторы 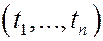 с неотрицательными компонентами.
с неотрицательными компонентами.
5. Производят стрельбу по мишени. Связав с мишенью декартову систему координат, можно отождествить с любым исходом испытания точку (x,y) координатной плоскости.
6. Датчик записывает температурный режим в плавильной печи за время Т плавки. Исходом этого испытания является функция 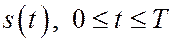 .
.
Попытаемся найти общие черты приведенных примеров реальных испытаний.
1) В каждом испытании имеется определенное пространство 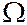 возможных исходов
возможных исходов 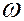 испытания, называемых элементарными исходами.
испытания, называемых элементарными исходами.
В примере 1: 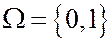 ,
,
в примере 2: 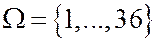 ,
,
в примере 3: 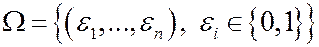 ,
,
в примере 4: 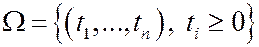 ,
,
в примере 5: 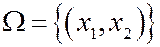 ,
,
в примере 6: 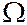 есть множество непрерывных функций на отрезке [0,T].
есть множество непрерывных функций на отрезке [0,T].
2) Исходы испытания не детерминированы.
3) Существует объективная мера возможности различных исходов испытаний.
Множество 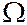 всех возможных элементарных исходов
всех возможных элементарных исходов  испытания будем называть пространством элементарных событий.
испытания будем называть пространством элементарных событий.
Введем понятие случайного события А, как подмножества пространства элементарных событий 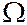 . Событие
. Событие 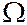 происходит в каждом испытании и его будем называть достоверным. Событие
происходит в каждом испытании и его будем называть достоверным. Событие 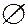 никогда не происходит и его будем называть невозможным.
никогда не происходит и его будем называть невозможным.
Определив события в терминах теории множеств, мы можем ввести для событий обычные операции теории множеств, которые для событий имеют свой смысл:
1. 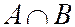 или
или 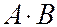 - пересечение множеств А и В, соответствует случаю когда в опыте происходят события А и В. События А и В называются несовместными, если
- пересечение множеств А и В, соответствует случаю когда в опыте происходят события А и В. События А и В называются несовместными, если 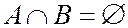 .
.
2. 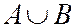 или
или 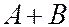 - объединение множеств А и В, соответствует случаю когда в опыте происходит хотя бы одно из событий А, В.
- объединение множеств А и В, соответствует случаю когда в опыте происходит хотя бы одно из событий А, В.
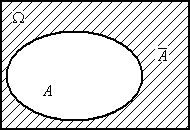
3. 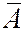 - событие, включающее все
- событие, включающее все 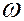 не входящие в А и только их. Событие
не входящие в А и только их. Событие 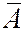 называется противоположным к А событием и соответствует случаю, когда в опыте событие А не происходит.
называется противоположным к А событием и соответствует случаю, когда в опыте событие А не происходит.
4. 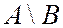 или
или 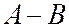 - событие, включающее все
- событие, включающее все 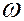 , которые принадлежат А и не принадлежат В. Событие
, которые принадлежат А и не принадлежат В. Событие 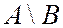 называется разностью событий А и В и соответствует случаю, когда в опыте событие А происходит, а событие В - нет. Легко видеть, что
называется разностью событий А и В и соответствует случаю, когда в опыте событие А происходит, а событие В - нет. Легко видеть, что 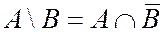 .
.
5. Симметрической разностью событий A и B называется событие 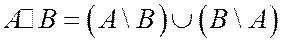 .
.
6. Для событий можно определить также отношение следования: 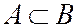 . Это означает, что если в опыте происходит событие А, то обязательно происходит и событие В (событие А влечет событие В).
. Это означает, что если в опыте происходит событие А, то обязательно происходит и событие В (событие А влечет событие В).
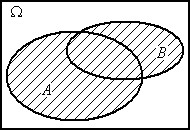
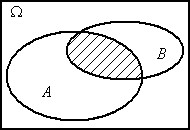
A+B AB 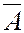
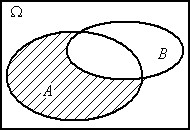
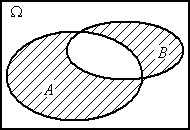
A–B 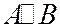
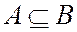
Рис. 1. Операции над событиями (результат – заштрихованная область)
Пример.
Рассмотрим опыт с бросанием 2-х игральных костей.
В данном случае пространство элементарных событий  соответствует множеству пар чисел (i,j), где i -число очков, выпавших на 1-ой кости, а j – на второй;
соответствует множеству пар чисел (i,j), где i -число очков, выпавших на 1-ой кости, а j – на второй; 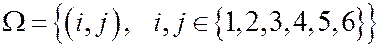 .
.
Введем события А – выпадает четная сумма очков, А1 – на каждой грани выпадает четное число очков, А2 – на каждой грани выпадает нечетное число очков.
Легко видеть, что
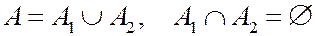 ,
,
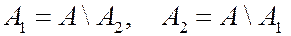 .
.
События 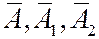 обозначают: выпадает нечетная сумма очков, хотя бы на одной грани выпадает нечетное число очков, хотя бы на одной грани выпадает четное число очков.
обозначают: выпадает нечетная сумма очков, хотя бы на одной грани выпадает нечетное число очков, хотя бы на одной грани выпадает четное число очков.
Используя формулу 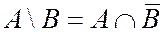 , получим
, получим
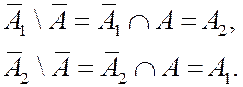
Действительно, рассмотрим первое из вышеприведенных выражений: 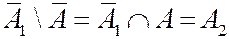 .
.
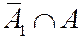 означает, что «хотя бы на одной грани выпадает нечетное число очков» и «выпадает нечетная сумма», что возможно только когда на «на каждой грани выпадает нечетное число очков», то есть
означает, что «хотя бы на одной грани выпадает нечетное число очков» и «выпадает нечетная сумма», что возможно только когда на «на каждой грани выпадает нечетное число очков», то есть 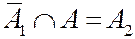 .
.
Основные свойства операций над событиями
1. А+В=В+А, АВ=ВА - коммутативность
2. А+(В+С)=(А+В)+С=А+В+С,
А(ВС)=А(ВС)=АВС - ассоциативность
3. А(В+С)=АС+ВС – дистрибутивность
4. А+А=А, АА=А
5. 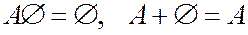
6. 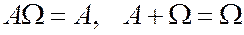
7. 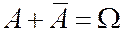
|
из
5.00
|
Обсуждение в статье: Основные свойства операций над событиями |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

