Кривая нормального распределения

Лекция 3

Числовые характеристики наблюдений.

Вычисления среднего арифметического для несгруппированных данных (или если частоты равны единице) производится по формуле:

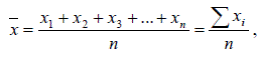
где n – объем наблюдений; х_i – варианты наблюдений; Σ - знак суммирования.

Если данные сгруппированы (частоты различны), то применяется формула:

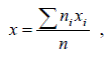
где n_i – частоты разрядов; x_i – срединные значение разрядов.

Модой называют результат выборки или совокупности наиболее часто встречающийся в этой выборке. Для интервального ряда модальный интервал выбирается по наибольшей частоте.

Медиана представляет собой результат измерения, который находится в середине ранжированного ряда.

Для того, чтобы увидеть в каком диапазоне рассеяны найденные значения признака, вычисляют характеристики рассеяния: размах варьирования, дисперсию s²; среднее квадратическое отклонение или стандартное отклонение s; коэффициент вариации V.

Размах варьирования – определяется разностью между наибольшим и наименьшим результатами наблюдений.

Дисперсия для несгруппированных данных вычисляется по формуле:

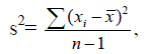
Или в преобразованном виде:

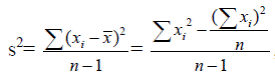
Для сгруппированных данных:

.

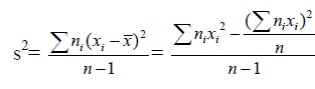Среднее квадратическое отклонение или стандартное отклонение s рассчитывается по формуле:

.

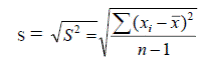Среднее квадратическое отклонение имеет ту же размерность, что и результаты измерений, то есть оно характеризует степень отклонения результатов от среднего значения.

В практической статистике часто требуется определить уровень однородности выборочных наблюдений. Для этого используется безразмерный показатель – коэффициент вариации V:

.

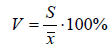Считается, что если коэффициент вариации не превышает 10%, то наблюдения можно считать однородными. Кроме того, коэффициент вариации часто используется при сопоставлении (сравнении) степени варьирования различных признаков, выраженных в различных единицах измерения.

Кривая нормального распределения.

Теоретическое распределение – распределение генеральной совокупности. Эмпирическое распределение – распределение выборки. Теоретическое распределение большинства измерений описывается формулой нормального распределения.

.

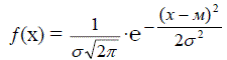График имеет вид:

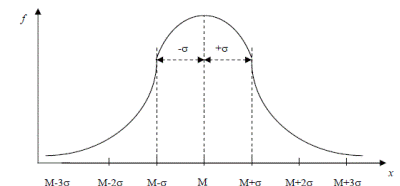
По графику плотности нормального распределения видно, что форма кривой зависит от параметров – μ и σ, которые могут принимать любые значения. Следовательно, с каждым новым значение μ и σ будет возникать новая совокупность нормально распределенных данных. Поэтому используют нормированное распределение с параметрами: μ=0; σ=1. Для этого вводят обозначения:

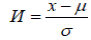
Плотность распределения вероятностей нормированного нормального распределения записывается выражением:

.

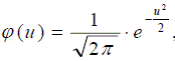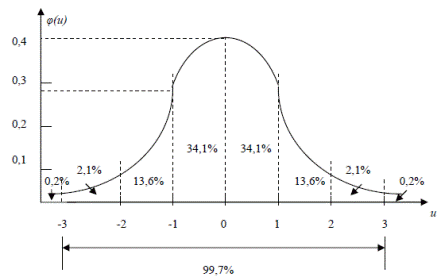
Вероятности попадания нормально распределенной случайной величины

в заданный интервал:

То есть, отклонения большие, чем 3σ следует ожидать в трех случаях из 1000. Это соотношение называют «правилом трех сигм» и используют при исключении сильно отклоняющихся результатов измерений, считая их ошибочными.