 |
Главная |
Оценка параметров генеральной совокупности
|
из
5.00
|
Характеристики генеральной совокупности принято обозначать буквами греческого алфавита: M – генеральное среднее арифметическое, G – генеральное стандартное отклонение и т.д., характеристики выборки обозначаются латинскими буквами: х – среднее арифметическое выборки, s – стандартное отклонение выборки. По отношению к характеристикам генеральной совокупности выборочные характеристики являются случайными и могут не совпадать с генеральными. Экспериментально проверить это утверждение невозможно, поскольку неизвестны истинные значения параметров генеральной совокупности.
Поэтому в математической статистике принято давать оценку генеральным параметрам по их выборочным значениям. Используемые для этого методы теории статистических выводов подразделяются на 2 класса: оценка параметров и проверка гипотез.
Оценка параметра – это определённая числовая характеристика, полученная из выборки. Когда оценка определяется одним числом, её называют точечной оценкой. В качестве точечных оценок параметров генеральной совокупности используются соответствующие выборочные характеристики.
Так как выборочная совокупность это часть генеральной совокупности, то естественно, что выборочные характеристики не будут точно совпадать с соответствующими генеральными. Например, если вычислить несколько х и s, используя разные группы испытуемых одной и той же совокупности, то закономерно, полученные средние арифметические выборок х будут варьировать вокруг генерального среднего арифметического M в n раз меньше, чем отдельные варианты выборки. В связи с этим, для вычисления ошибки, которая неизбежно возникает при вычислении M по выборочным оценкам х , рекомендуется применять формулу:
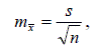
где mx - стандартная ошибка среднего арифметического; s – выборочное стандартное отклонение, n – объем выборки. Из формулы видно, что с увеличением объема выборки снижается стандартная ошибка среднего арифметического.
Величина mx показывает, какая ошибка в среднем допускается, если использовать вместо генерального среднего M его выборочную оценку х . Поэтому вычисленное среднее арифметическое в научных работах записывают следующим образом:
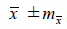 .
.
Кроме того, в практике физической культуры и спорта значительный интерес при оценке параметров генеральной совокупности представляет определение границ доверительного интервала, в который попадает истинное значение среднего арифметического изучаемой совокупности.
Доверительный интервал- это интервал, в котором с заданной вероятностью находится истинное значение параметра генеральной совокупности.
Вероятности, признанные достаточным для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик, называют
доверительными. Обычно, в качестве доверительных вероятностей выбирают значения 0,95; 0,99; 0,999 (их принято выражать в процентах – 95%, 99%, 99,9%).
Для оценки среднего генеральной совокупности доверительный интервал имеет вид:
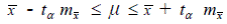 ,
,
где tα – нормированное отклонение, определяемое выбранной доверительной вероятностью. Значение tα для стандартных значений α (0,05; 0,01;0,001) и различных значений параметра (ƒ )t – распределения (ƒ = n-1), приведены в таблицах t – распределения Стьюдента.
С учетом выражения для ошибки среднего выражение можно переписать в виде:
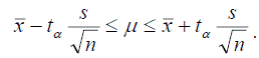
При больших объемах выборки (n≥ 30) t –распределение Стьюдента переходит в нормальное. Поэтому доверительный интервал для μ при n ≥ 30 можно записать следующим образом:
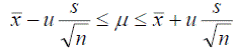 .
.
Доверительный интервал для дисперсии имеет вид:
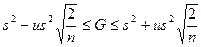
|
из
5.00
|
Обсуждение в статье: Оценка параметров генеральной совокупности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

