 |
Главная |
Параметры «минимаксной» стратегии
|
из
5.00
|
| № | Показатель | Формулы для расчета параметров стратегии |
| Интервал между проверками уровня запаса – Δ | - определяется в соответствии с условиями работы склада компании и уровнем автоматизации; может быть непрерывным (в режиме on-line) в случае соответствующего информационного обеспечения склада (Δ→0); может быть периодическим, например, через день, или 1 раз в неделю (Δ = const). | |
| Время выполнения поставки – L, дней | - определяется статистически на основе данных по прошлым поставкам:
 или или  ,
где li – значение времени выполнения i-й поставки, дней;
Qi – величина i-й поставки, ед.; ,
где li – значение времени выполнения i-й поставки, дней;
Qi – величина i-й поставки, ед.;
| |
| Возможное время задержки поставки – τ (σL), дней. | - рассчитывается на основании данных о предыдущих поставках:
 или или 
| |
| Интенсивность потребления – d, ед./день | - среднее значение:
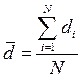 ,
где di – расход в i-й момент времени; N – объем выборки ,
где di – расход в i-й момент времени; N – объем выборки
| |
| СКО интенсивности потребления – σd | - среднее квадратическое отклонение от среднего расхода: 
| |
| Потребление за время поставки – d(L), ед. | - можно использовать формулы:
 - среднее - среднее
 - максимальное - максимальное
| |
| Страховой запас – Sс, ед. |
 ,
где хp – параметр, соответствующий вероятности отсутствия дефицита. ,
где хp – параметр, соответствующий вероятности отсутствия дефицита.
| |
| Smin – пороговый уровень запаса, ед. | 
| |
| Максимально желаемый объем запаса– Smax , ед. |  ,
где ,
где 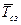 - среднее значение периода времени между смежными заказами, дней. - среднее значение периода времени между смежными заказами, дней.
| |
| Размер заказа - Qз, ед. |  ,
где Qзi – размер заказа в момент времени i;
Sm – текущий запас, который ≤ пороговому (минимальному) уровеню запаса;
ЗПi – запас в пути на момент времени i. ,
где Qзi – размер заказа в момент времени i;
Sm – текущий запас, который ≤ пороговому (минимальному) уровеню запаса;
ЗПi – запас в пути на момент времени i.
|
Пример 2.4:
Воспользуемся исходными данными из примера 2.1 о параметрах реализации товара «Х» и смоделируем действие (s; S)-стратегии для периода в 46 дней.
Расчет страхового запаса осуществим по формуле:
 (2.15)
(2.15)
Получаем:

Верхнюю границу уровня запасов (Smax) будем рассчитывать по формуле:
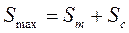 , (2.16)
, (2.16)
где Sт – текущий запас. В качестве текущего запаса целесообразно использовать величину оптимального размера заказа (Qopt). Величина оптимального размера заказа была рассчитана в примере 2.2. Qopt = 86 ед.
Таким образом, начальный (максимальный) запас в системе будет: 
Нижняя граница уровня запасов (Smin) рассчитывается по формуле:
 (2.17)
(2.17)
Таким образом:
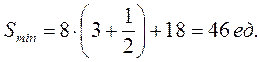
Расчет величины заказов на пополнение запаса осуществляется по формуле:
 , (2.18)
, (2.18)
где  (см. пример 9.1).
(см. пример 9.1).
Допустим, что в данном примере проверки уровня запаса на сладе осуществляются на начало дня.
Результаты моделирования «минимаксной» стратегии представлены в табл. 2.8.
На начало 8-го дня уровень запаса достиг 39 ед., что меньше минимального уровня  Следовательно, на 8-й день размещается заказ, размер которого определяется по формуле (2.18).
Следовательно, на 8-й день размещается заказ, размер которого определяется по формуле (2.18).

Срок выполнения которого, по аналогии с примерами 9.1,9.2 и 9.3 составит 3 дня (L1=3 дн.). Заказ выполняется в течении 8-го, 9-го и 10-го дня и поступает на склад на 11-й день.
Следующий момент размещения заказа наступает на 18-й день (начало дня), когда уровень запаса на складе достигает 38 ед. Величина заказа составит 90 ед.

Время выполнения второго заказа L2=4дня (18-й, 19-й, 20-й и 21-й день), т.о. второй заказ поступит на склад на 22 день.
Третий заказ размещается на 27-й день (начало дня), когда уровень запасов достигнет 45 ед. Величина третьего заказа составляет 83 ед.

Выполняется третий заказ в течении 1-го дня (L3=1) и поступает на склад на 28-й день.
Четвертый заказ размещается на 37-й день (начало дня), когда уровень запасов достигнет 39 ед., выполняется четвертый заказ в течении трех дней (L4=3) и поступает на склад на 40-й день и т.д. Величина четвертого заказа составляет 89 ед.

Результаты моделирования действия «минимаксной» стратегии приведены в табл. 2.8 и на рис. 2.9.
Таблица 2.8
Результаты моделирования действия «минимаксной» стратегии
| Номер дня | Спрос di | Запас на складе, ед. | Дефицит (прогноз), ед. | Величина заказа | Величина поставки | ||
| на начало дня | на конец дня | на начало дня | на конец дня | ||||
| И т.д. | … | … | … | … | … | … | … |

Рис. 2.9. «Минимаксная стратегия»
Таким образом вам необходимо на основе исходных данных, смоделированных на первом этапе (раздел 1 курсовой работы), рассчитать параметры «минимаксной» стратегии (табл. 2.7), осуществить моделирование действия данной стратегии (как показано в примере 2.4) и построить соответствующий график как на рис. 2.9.
2.3. Расчет страхового запаса в стратегиях:
Для расчета величины страхового запаса в условиях неопределенности может быть использована формула Феттера:
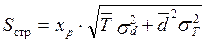 , (2.19)
, (2.19)
где xp– параметр нормального закона распределения, соответствующий вероятности отсутствия дефицита продукции на складе P(х) (табл. 2.9, рис. 8.2)
 - среднее значение продолжительности функционального цикла (период времени между поставками);
- среднее значение продолжительности функционального цикла (период времени между поставками);
 - среднесуточный расход запаса;
- среднесуточный расход запаса;
σТ, σd – соответственно средние квадратические отклонения случайных величин T и d.
Таблица 2.9
Соотношение уровня обслуживания и величины множителя
для страхового запаса
| Уровень обслуживания с заданной вероятностью попадания в границы Р(tв), % | Значение коэффициента хр |
| 0,8 | 1,282 |
| 0,84 | 1,404 |
| 0,88 | 1,554 |
| 0,9 | 1,643 |
| 0,92 | 1,75 |
| 0,96 | 2,053 |
| 0,98 | 2,325 |
| 0,998 | 3,29 |
Дополнительное задание:
|
из
5.00
|
Обсуждение в статье: Параметры «минимаксной» стратегии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

