 |
Главная |
НЕУСТОЙЧИВОСТЬ ТЕЧЕНИЯ В ПОДШИПНИКАХ
|
из
5.00
|
Подшипники скольжения могут быть источниками автоколебаний с повышенными амплитудами.
Закономерности течения в тонком масляном слое рассмотрим на примере двух относительно движущихся пластин 1 и 2, изображенных на схеме (рис). Зазор между пластинами h много меньше их продольных размеров.
Рисунок!
Зазор h полагаем переменным вдоль по координате x, а пространство между поверхностями – заполненным вязкой несжимаемой жидкостью. Задача заключается в определении поля давлений, вызываемого движением ограничивающих поверхностей А и В. Пластина 2 перемещается вдоль оси x со скоростью U2 и в направлении оси y co скоростью V. Движение жидкости при сделанных допущениях может быть представлено дифференциальным уравнением неразрывности:
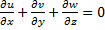 ; (1)
; (1)
и уравнениями движения Навье-Стокса:
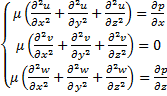 ; (2)
; (2)
Соответствующие ускорениям силы инерции малы по сравнению с силами вязкости и поэтому указанные составляющие отброшены. Так как реализуется течение в щели, производные 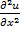 и
и 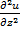 много меньше
много меньше 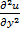 . Аналогичный вывод можно сделать относительно производных от v и w. Поэтому уравнения (2) упрощаются:
. Аналогичный вывод можно сделать относительно производных от v и w. Поэтому уравнения (2) упрощаются:
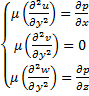 ; (3)
; (3)
Так как производные 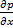 и
и 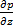 не зависят от y, эти уравнения могут быть проинтегрированы при следующих граничных условиях:
не зависят от y, эти уравнения могут быть проинтегрированы при следующих граничных условиях:
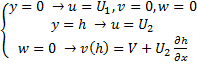 ; (4)
; (4)
Проинтегрировав первое уравнение из системы (3), получим:
 ; (5)
; (5)
 ; (6)
; (6)
Подставив первое граничное условие, получим 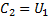 ; из второго имеем:
; из второго имеем: 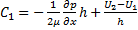 ; подставим значения постоянных в уравнение (6):
; подставим значения постоянных в уравнение (6):
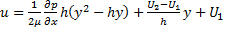 ; (7)
; (7)
В результате интегрирования второго и третьего уравнения из системы (3) и ряда преобразований получим:
 ; (8)
; (8)
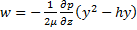 ; (9)
; (9)
После дифференцирования уравнений (7)-(9), подстановки в (1) и осреднения (интегрирования по высоте щели) получим:
 ; (10)
; (10)
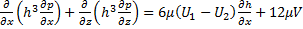 ; (11)
; (11)
Уравнение (11) связывает распределение давления с формой щели и движением ее ограничивающих поверхностей. В уравнении присутствует нормальная составляющая скорости V, которая не равна нулю при колебаниях ротора. При расчетах статических режимов принимают V=0. Если поверхность 1 неподвижна, то U1=0. Если пластина бесконечна то 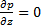 . Это позволяет привести уравнение (11) к виду:
. Это позволяет привести уравнение (11) к виду:
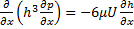 ; (12)
; (12)
Из уравнения (12) следует, что для создания гидродинамических подъемных сил в подшипнике необходимо образование масляного клина 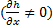 . При постоянном зазоре
. При постоянном зазоре 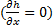 значения
значения 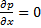 , а следовательно подъемная сила отсутствует.
, а следовательно подъемная сила отсутствует.
Рассмотрим случай плоского движения в соответствии со схемой на рис, где изображена пластина шириной  и перемещающаяся относительно нее плоскость. В данном случае пластина имитирует вкладыш упорного подшипника. Уравнение движения будет в виде (12), проинтегрировав которое получим:
и перемещающаяся относительно нее плоскость. В данном случае пластина имитирует вкладыш упорного подшипника. Уравнение движения будет в виде (12), проинтегрировав которое получим:
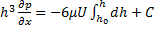 ; (13)
; (13)
Используя граничные условия:
- при x0 h=h0 , p=0;
- при xm h=hm, p=pmax, dp/dx=0;
получим  ; (14)
; (14)
В результате имеем  ; (15)
; (15)
Проинтегрировав (15), после ряда преобразований найдем
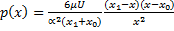 ; (16)
; (16)
Несущая способность элемента пластины единичной длины
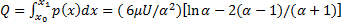 ; (17)
; (17)
Координата опоры вкладыша  может быть определена из уравнения моментов
может быть определена из уравнения моментов
 ; (18)
; (18)
Преобразуем уравнение (18)
 ; (19)
; (19)
Анализируя производную 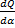 , находим максимум Q при α=2,2. Этому оптимальному соотношению будет соответствовать отношение для выбора точки опоры
, находим максимум Q при α=2,2. Этому оптимальному соотношению будет соответствовать отношение для выбора точки опоры 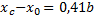 . Несущую способность опорного вкладыша конечной длины l необходимо определить с учетом распределения p(z), которое в первом приближении можно считать параболическим.
. Несущую способность опорного вкладыша конечной длины l необходимо определить с учетом распределения p(z), которое в первом приближении можно считать параболическим.
РАСЧЕТ ОПОРНОГО ПОДШИПНИКА
При расчетах подшипника обычно используется понятие коэффициента нагруженности (грузоподъемности), введение которого может быть обосновано анализом подобия процессов течения в слоях смазки. Исследуемые течения двух масляных слоев подобны, если параметры движения (давления, скорости, перемещения) для второго подшипника могут быть получены по параметрам первого подшипника путем умножения на масштабные коэффициенты. Воспользуемся уравнением Рейнольдса:
 ; (1)
; (1)
и, обозначив масштабные коэффициенты: линейных размеров Kx, зазоров Kh, давлений Kp, динамических вязкостей Kµ, угловых скоростей Kω, найдем масштабные коэффициенты и необходимые критерии. Для двух различных подшипников произведения масштабных коэффициентов будут равны 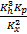 для первого члена в левой части и
для первого члена в левой части и 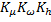 для первого члена в правой части, а их отношение
для первого члена в правой части, а их отношение 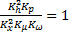 . Следовательно, можно записать выражение для безразмерного критерия подобия:
. Следовательно, можно записать выражение для безразмерного критерия подобия:
 ; (2)
; (2)
Умножив и разделив на ld, получим коэффициент нагруженности 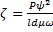 , где
, где 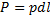 – радиальное усилие на подшипник. Однако величина ζ в этом виде получена из условия одномерности, и для уточнения к этой характеристике должны быть добавлены геометрические параметры
– радиальное усилие на подшипник. Однако величина ζ в этом виде получена из условия одномерности, и для уточнения к этой характеристике должны быть добавлены геометрические параметры  - относительный эксцентриситет,
- относительный эксцентриситет,  – относительная длина и α – угол охвата, без которых представление p через отношение
– относительная длина и α – угол охвата, без которых представление p через отношение 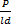 и величины h через δ будет характеризоваться неопределенностью. Отметим, что неопределенность таким добавлением параметров не устраняется полностью, так как при этом не учитывается реальный характер эпюры давлений. Геометрически должны быть подобны камеры подвода и отвода масла, полости охлаждения и др. Поэтому используются специальные функции Φ1, Φ2 и Φ3, подтверждаемые экспериментально.
и величины h через δ будет характеризоваться неопределенностью. Отметим, что неопределенность таким добавлением параметров не устраняется полностью, так как при этом не учитывается реальный характер эпюры давлений. Геометрически должны быть подобны камеры подвода и отвода масла, полости охлаждения и др. Поэтому используются специальные функции Φ1, Φ2 и Φ3, подтверждаемые экспериментально.
При расчетах стационарного режима 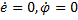 и, следовательно,
и, следовательно,
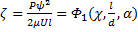 ; (3)
; (3)
Формула (3) иллюстрирует взаимосвязанность основных факторов, влияющих на процесс смазки. Отсюда следует, что грузоподъемность подшипника растет с увеличением µ, и падает с увеличением относительного зазора ψ.
Необходимый объемный расход масла определяется по формуле
 , (4)
, (4)
где 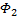 – безразмерный коэффициент расхода, определяется по графику.
– безразмерный коэффициент расхода, определяется по графику.
 ; (5)
; (5)
В формуле (5) преобразования выполнялись с учетом 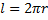 ;
; 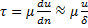 .
.
 ; (6)
; (6)
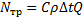 ; (7)
; (7)
|
из
5.00
|
Обсуждение в статье: НЕУСТОЙЧИВОСТЬ ТЕЧЕНИЯ В ПОДШИПНИКАХ |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

