СООТНОШЕНИЯ МЕЖДУ АМПЛИТУДАМИ КОЛЕБАНИЙ РОТОРА И ОПОР

Движение ротора по амплитуде может отличаться от движения опор. Рассмотрим колебания ротора, состоящего из упругого вала с одним диском, расположенным посередине между упругими и инерционными опорами. Будем также учитывать упругость масляного слоя в подшипниках. Предположим, что ротор колеблется по первой форме и колебания левой и правой опоры одинаковы, (плоскопараллельное движение системы).

Рис. 1. Схема для определения соотношений между амплитудами колебаний ротора и опор в рассматриваемом случае

Рассмотрим колебания ротора и опор без учета сил сопротивления. Для нахождения соотношения между амплитудами колебаний ротора и опор в данном случае перейдем от схемы, изображенной на рис. 1, к схемам, изображенным на рис. 2.

Рис. 2. Схемы к определению соотношений между амплитудами колебаний ротора и опор в случае, когда силы сопротивления не учитываются: а) - для составления уравнений движения; б) - для записи замыкающего соотношения

Для решения поставленной задачи при трех неизвестных перемещениях ( ) необходимо иметь систему из трех уравнений. Составим дифференциальные уравнения движения:

- для диска

; (1)

- для опоры

; (2)

где - половина реальной массы диска, кг; - масса одной опоры, кг; - время, c;

Для замыкания данной системы уравнений, пользуясь схемой, изображенной на рис. 2б, мы можем записать следующее соотношение

; (3)

- изгибная жесткость вала, Н/м; - жесткость опор, Н/м; - жесткость масляного слоя, Н/м; w - угловая скорость вращения вала, рад/с; e - эксцентриситет, м; 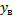- перемещение середины вала, м; - перемещение конца вала, м; - перемещение вкладыша опоры, м.

Частные решения:

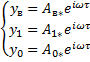; (4)

где , , - комплексные амплитуды перемещения середины вала, конца вала и вкладыша опоры соответственно, м.

Подставив (4) в (1), (2), (3) и сократив на 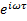, получим

; (5)

Неизвестными в системе из уравнений (5) являются три величины комплексных амплитуд. Составим главный определитель системы, состоящий из коэффициентов при неизвестных в системе однородных уравнений

; (6)

Значение любого из неизвестных можно найти, разделив определитель, полученный из главного определителя заменой соответствующего столбца из коэффициентов при неизвестном на столбец свободных членов, на главный определитель системы

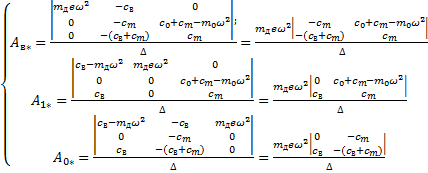; (7)

Теперь мы можем оценить значение отношений амплитуд и . Разница комплексных амплитуд и пропорциональна напряжениям изгиба в вале. Поэтому может представлять интерес значение следующего отношения .

В полученных выше уравнениях не учитывались силы сопротивления, которые могут оказывать существенное влияние при колебаниях в околорезонансной области.

Рассмотрим колебания ротора и опор с учетом сил сопротивления

Для нахождения соотношения между амплитудами колебаний ротора и опор в данном случае перейдем от схемы, изображенной на рис. 1, к схеме, изображенной на рис. 3.

Рис. 3. К определению соотношения между амплитудами колебаний ротора и опор в случае, когда силы сопротивления учитываются

Учет вязкого сопротивления произведем введением в схему, изображенную на рис. 2а демпферов (рис.3).

Перепишем теперь уравнения (1), (2) и (3) с учетом влияния сил вязкого сопротивления

; (8)

Подставив выражения (4) для перемещений в (8) и сократив на 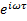, получим

; (9)

Неизвестными в системе уравнений (9) являются три величины комплексных амплитуд. Составим главный определитель, состоящий из коэффициентов при неизвестных для системы однородных уравнений

Значения комплексных амплитуд , и можно определить с использованием теоремы Крамера. Теперь можно определить значение мнимых и действительных частей комплексных амплитуд , и , и, следовательно, значение их модулей. Тогда значение угла сдвига по фазе g для любой из амплитуд можно найти как арктангенс отношения значения мнимой части амплитуды к ее действительной части. Окончательно, мы можем оценить значение отношения амплитуд и , а также отношения .