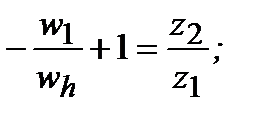Краткие сведения о контактных напряжениях

Контактные напряжения возникают при взаимодействии тел, размеры площадки контакта которых малы по сравнению с размерами самих соприкасающихся тел, например, контакт двух стальных­ кру­говых цилиндров по общей образующей (рис. 1.4) (ана­лог зубчатого зацепле­ния, фри­к­­ционной пере­дачи).

 

 

 

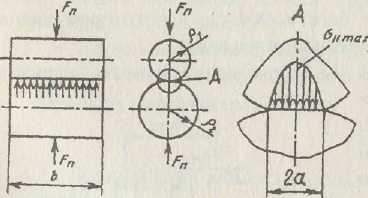
Рис. 1.4. Контакт двух стальных цилиндров

 

Контакт при перекатывании в передачах происхо­дит по малым площадкам (начальный контакт по линии или в точ­ке), из-за чего в поверхностном слое возникают высокие на­пряжения. Материал в районе этой площадки испытывает объемное напряженное состояние. Впервые исследованием контактных на­пряжений занимался физик Герц (Hertz или Herz). В его честь в расчетах на контактную прочность все параметры обозначают индексом Н: например, σ_Н .

Контакт ненагруженных прижимающей силой цилиндров с па­раллельными осями происходит по линии (по образующей). Под действием прижимающей силы F_n, вследствие упругих деформаций цилиндров первоначальный контакт по линии переходит в контакт по прямоугольной площадке (очень узкой полоске) шириной 2а. Размеры площадки контакта и возникающие нормальные напряже­ния σ_Н зависят от нагрузки F_n, упругих характеристик материалов (коэффициентов Пуассона, модулей упругости) и формы контакти­рующих тел. В поперечном сечении по площадке контакта напряжения изменяются по эллиптическому закону, достигая максимального значения σ_{Н mах} в зоне максималь­ных деформаций – по линии действия прижимающей силы (вынос­ной элемент А). Особенностью действия нормальных контактных напряжений является то, что они не распространяются глубоко в тело деталей, сосредоточиваясь в тонком поверхностном слое.

Кроме нормального напряжения σ_Н в зоне контакта возникают также касательные напряжения τ. Наибольшее касательное напря­жение τ _mах = 0,3 σ_{Н mах} имеет место в точке, расположенной на линии действия прижимающей силы F_n и отстоящей от поверхности со­прикосновения на 0,78а.

Числовые значения контактных напряжений намного превы­шают значения других видов напряжений (растяжения, изгиба) и механических характеристик материала σ_т и σ_в. Отсутствие мгновенного разрушения при наличии таких высоких напряжений объясняются тем, что в зоне их действия материал находится в условиях всестороннего объемного сжатия.

Максимальное значение σ_{Н mах} используют в качестве основного критерия контактной прочности:

σ_{Н mах} ≤ [σ_Н],

 

где [σ]_Н – допускаемое контактное напряжение.

Для вычисления максимального контактного напряжения на площадке контакта используют формулу Герца, полученную из решения контактной задачи теории упругости (индекс "max" при этом опускают):

 

.

ПЛАНЕТАРНЫЕ ПЕРЕДАЧИ

2.1. Общие сведения

Планетарныминазывают передачи, имеющие зубчатые колеса с перемещающимися осями. Наиболее широко применяют простую одно­ряднуюпередачу(рис. 2.1), которая состоит из центрального вращающегося колеса ас неподвижной геометрической осью и наружными зубьями, неподвижного центрального колеса b(колесо соединено с корпусом)с внутренними зубьями, сателлитов g– колес с наружными зубья­ми, которые зацепляются одновременно с колесами аи b(число сателлитов n_wв передаче может быть от 3 до 6, на рисунке n_w = 3), и водила h, на котором расположены оси сателлитов. Водило соединено с тихоходным валом.

Рис. 2.1. Планетарные передачи:

а – конструктивная схема, б – кинематическая схема

 

Передача работает следующим образом: при неподвижном колесе bвращение колеса а вызывает вращение сателлита g относительно собственной оси, а обкатывание сателлита по колесу bперемещает его ось и вращает водило h. Сателлит совершает вращение относительно водила и вме­сте с водилом вращается вокруг центральной оси. Движение сателлитов схоже с движением планет вокруг Солнца, поэтому передачи назвали планетарными.

При неподвижном колесе b чащеведущим бывает центральное колесо а(тогда движение передаются oт колеса ак водилу h), но возможна передача движения и от водила h к колесу а.

При неподвижном колесе bведущим в планетарной передаче может быть (чаще всего) центральное колесо а(и тогда движение передается oт колеса ак водилу h) или водило (и тогда движение передается от водила h к колесу а).

Основными звеньямипланетарной передачи являются звенья, воспринимающие внешние вращающие моменты. На рис. 2.1. основные звенья а, b, h– два центральных колеса (2К) и водило (h). Кратко такую передачу обозначают как «2К-h». Внешние моменты на звеньях обозначают: Т_а–момент на ведущем валу, Т_b – момент на неподвижном колесе b (на корпусе),T_h – на ведомом (тихоходном) валу.

Следует иметь ввиду:

· в планетарных передачах применяют не только цилиндрические, но и конические колеса с прямым или косым зубом;

· для наиболее часто применяемых схем передач характерно наличие либо высокого КПД, либо большого передаточного отношения в одной передаче;

· для получения больших передаточных отношений в силовых приводах применяют многоступенчатые планетарные передачи.

 

Достоинствамипланетарных передач являются:

· широкие кинематические возможности, позволяющие использовать их в силовых передачах и приборах в качестве редуктора с постоянным передаточным отношением (в передаче, изображенной на рис. 2.1. при заданной угловой скорости ведущего звена угловые скорости всех остальных звеньев принимают вполне конкретные значения, поэтому рассматриваемая передача имеет постоянное передаточное число); в качестве коробки скоростей, передаточное отношение в которой изменяют путем поочередного торможения различных звеньев; в качестве дифференциального механизма в автомобилях, тракторах, станках, приборах (см. ниже); часто применяют планетарную передачу, совмещенную с элек­тродвигателем (мотор-редуктор, мотор-колесо);

· компактность и малая масса (масса по сравнению с непланетарными зубчатыми может быть уменьшена в 2–4 раза), так как передаваемая мощность распределяется по нескольким потокам (равным числу сателлитов), что позволяет снизить нагрузку на зубья в каждом зацеплении в несколько раз;

внутренне зацепление (колеса b и g) обладает повышенной нагрузочной способностью, т.к. у него больший приведенный радиус кривизны в зацеплении (см. знаки « ±» в формуле определения приведенного радиуса кривизны);

· большие передаточные отношения при малом числе колес (до тысячи и больше) без применения многоступенчатых передач (но нужно помнить, что с увеличением передаточного отношения в одной передаче КПД уменьшается);

· малая нагрузка на опоры, т.к. при симметричном расположении сателлитов радиальные нагрузки на валы и их опоры уравновешиваются;

· работа с мень­шим шумом по сравнению с обычными зубчатыми передачами за счет повышенной плавности внутреннего зацепления, замыкания сил в механизме, обуславливающими передачу меньших сил на корпус.

К недостаткам планетарных передач относятся:

· повышенные требования к точности изготовления и монтажа;

· большое число подшипников качения;

· необходимость использования долбяка (зубодолбежных станков) для нарезания колес с внутренними зубьями.

Если в планетарной передаче создать условия, когда все основные звенья подвижны (освободив неподвижное колесо и придав ему вращение), передачу называют дифференциальной: такая передача позволяет суммировать движения двух звеньев на одном или раскладывать движения одного звена на два остальных (рис. 2.2).

 

Рис. 2.2. Планетарные дифференциальные передачи:

а – суммирующая скорости движения, б – раскладывающая скорости движения

 

Схема, приведенная на рис. 2.2, а, обеспечивает суммирование движений звена а (двигатель Д₁) и звена b (двигатель Д₂) на водиле h. Здесь между двигателем Д₂ и колесом b поставлена дополнительная передача z₁, z₂ для получения необходимого вращающего момента на колесе b.Схема применяется в системах автоматического управления.

Схема, приведенная на рис. 2.2, б, представляет собой дифференциал заднего моста автомобиля. Он состоит из конических зубчатых колес, которые насаживаются на ведущие полуоси автомобиля и сцепляются с сателлитом g, свободно сидящим на оси, закрепленной во вращающемся водиле h. Двигатель приводит водило в движение посредством конической зубчатой пары z₁, z₂ . Пока автомобиль движется по прямой дороге, силы сцепления колес с дорогой одинаковы, угловые скорости полуосей также одинаковы и равны угловой скорости водила. На закруглённом участке дороги колесо, движущееся по внешней кривой, проходит больший путь, чем колесо, движущееся по внутренней кривой. Если бы оба колеса автомобиля были закреплены на одной оси, то наблюдалось бы скольжение покрышек по дороге, что обусловливало бы их значительный износ. При использовании дифференциала сателлит g обкатывает колеса и одновременно вращается вокруг своей оси, в результате чего угловые скорости полуосей и ведущих колес автомобиля оказываются различными (т.е. при повороте одно колесо вращается быстрее другого). Скольжение покрышек по дороге прекращается или сводится к минимуму.

 

2.2. Передаточное отношение

При определении передаточного отношения планетарной пере­дачи используют метод Виллиса (метод остановки водила): всей планетарной передаче мысленно сообщают допол­нительно вращение с угловой скоростью водила w_h, но в обратном направлении. При этом водило как бы останавливается, а закреплен­ное колесо освобождается. Полученный при этом обращенный механизм (скорость водила 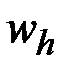= 0)представляет собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами, т.е. колесами, не влияющими на передаточное отношение механизма. Передаточное отношение в обращенном механизме оп­ределяют как в двухступенчатой передаче с одним внешним и одним внутренним зацеплением. Передаточное отношение определяют буквой с индексами, например , где нижние индексы – соответственно ведущее и ведомое звено, верхний – звено, обычно неподвижное, относительно которого рассматривается движение.

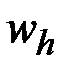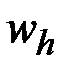
Пусть для дифференциального механизма, изображенного на рис. 2.1 основные звенья имеют положительные угловые скорости , , . Остановим водило, т.е. сообщим мысленно механизму скорость . После этого скорости звеньев изменятся и будут равны соответственно , , = 0.

Передаточное отношение примет выражение

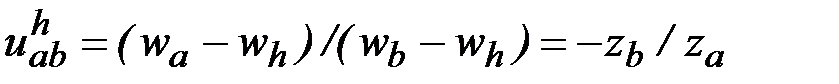, (2.1)

где и – соответственно угловые скорости колес а и b относительно водила, и числа зубьев колес aи b.

Передаточное отношение

имеет знак «–» для внешнего зацепления (ведущее и ведомые звенья вращаются в разные стороны) и имеет знак «+» для внутреннего зацепления (ведущее и ведомые звенья вращаются в одну сторону).

В планетарной передаче любое основное звено может быть ос­тановлено.

Для планетарной передачи, у которой колесо bзакреплено в корпусе неподвижно (w_b = 0), колесо а является ведущим, а водило h– ведомым, из формулы (2.1) получим:

или

Отсюда следует

(2.2)

Для планетарной передачи, у которой колесо bзакреплено в корпусе неподвижно (w_b=0), водило h является ведущим, а колесо a – ведомым, имеем:

(2.3)

Таким образом, в зависимости от остановленного звена можно получить различные значения передаточного отношения планетар­ной передачи. Это свойство планетарных передач используют в ко­робках передач.

2.3. Вращающие моменты на основных звеньях

При установившемся движении для системы (рис. 2.1) справедливы два уравнения:

T_a+T_b+T_h = 0 (при установившемся движении система находится в равновесии ).

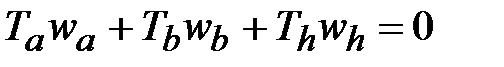(при установившемся движении из условия сохранения энергии).

При w_b = 0 имеем

и .

При передаче движения от ак h

,

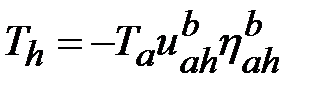где – коэффициент полезного действия, учитывающий потери при передаче движения.

Один из трех моментов (вращающий момент Т_а,Н∙м) определяется по известным мощности Р_а,кВт и частоте вращения п_а,мин^--1:

Два других находятся решением системы двух уравнений.

;

;

.

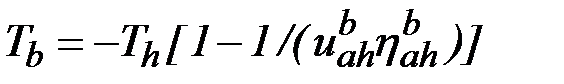Так как обычно велико, то вращающий момент на цен­тральном колесе b мало отличается от момента на выходном валу: . Знаки моментов на колесах а и b одинаковые, а на ведомом – противоположный.

2.4. Силы в зацеплении

Окружные силы в зацеплении вычисляют по вращающим мо­ментам (Н∙м) и делительным диаметрам d_a, d_b, d_g (мм) зубчатых ко­лес (для передач без смещения):

,

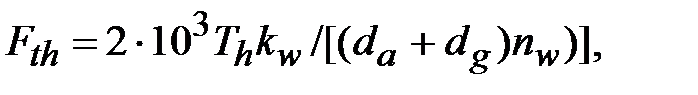
где n_w – число сателлитов, k_w – коэффи­циент, учитывающий неравномерность распределения нагрузки между сателли­тами (между потоками).

На рис. 2.3, а показаны силы, дейст­вующие на один из сателлитов. Ради­альные силы F_rb =F_tatga_w и F_rb = F_tb tga_w здесь уравновешены.

Рис. 2.3. Силы в зацеплениях сателлитов и методы их выравнивания:

а – силы в зацеплениях; б – многоугольник сил для центральных колес;
в – шарнирная подвеска центральных колес

Если бы передача была совершенной (k_w =1), окружные силы на колесе ав зацеплении со всеми сателлитами были бы одинаковы по величине: F_ta1= F_ta2= = F _ta3 (тонкие линии многоугольника сил на рис. 2.3, б); в реальности силы распределены неравномерно (сказываются неточность изготовления, деформации под нагрузкой): F_ta1 F_ta2 F _ta3 (жирные линии многоугольника сил на рис. 2.3, б). Равновесие обеспечивается уравновешивающей силой F_оп, возникающей в опоре центрального колеса. Значения коэффициента k_w при этом значительно больше единицы. Для уменьшения неравномер­ности распределения момента и выравнивания окружных сил колесо а выполняют без опор («плавающим») и соединяют его с ведущим валом с помощью зубчатой муфты, которая дает возможность компенсировать вероятные радиальные смещения шестерни (рис. 2.3, в). В этом случае колесо а под действием силы F_оп,самоустанавливается, стре­мясь достичь равновесного положения, преодолевая действие сил трения и инерции. При этом значения коэффициента k_w становятсязначительно меньше – k_w= 1,05 ... 1,15.

 

2.5. Особенности расчета планетарных передач

Расчет планетарных передач начинают с подбора чисел зубьев. Так как колеса взаимосвязаны, то наряду с выдержкой заданного передаточного отношения необходимо обеспечить следующие условия: соосности, симметричного расположения сателлитов, соседства.

Для приведенной выше схемы планетарной прямозубой передачи (рис. 2.1) без смещения эти условия достигаются выполнением следующих действий.

Число зубьев z_a центральной шестерни а задают из требованиянеподрезанияножки зуба: z_a 17. Принимают z_a =21…24 для Н 350 НВ; z_a = 18…21 для 35 HRC < Н < 52 HRC и z_a = 17 при Н> 52 HRC.

Число зубьев z_b неподвижного центрального колесаbопреде­ляют по заданному передаточному отношению u^b_ah из формулы: .

Число зубьев z_g сателлитаgвычисляют из условия соосности. Условие соосности требует равенства межосевых расстояний различных пар зацепляющихся колес.

(2.4)

где d = mz – делительный диаметр соответствующего зубчатого колеса. Так как модули зацеплений планетарной передачи одинаковы, то формула (2.4) принимает вид:

(2.5)

Полученные числа зубьев z_a, z_g, и z_b проверяют по условиям симметричного расположения сателлитов (условие сборки) и соседства.

Условие сборки симметричного расположения сателлитов требует, чтобы во всех зацеплениях централь­ных колес с сателлитами зубья одних совпадали с впадинамидругих (иначе собрать передачу нельзя). Проверено, что при симметричном расположении сателлитов условие сборки удовлетворяется, когда сумма зубьев центральных колес (z_a+z_b) кратна числу сателлитов n_w (обычно n_w=3), т.е. (z_a + z_b)/n_w равно целому числу.

Условие соседстватребует, чтобы сателлиты не задевали зубь­ями друг друга. Для этого необходимо, чтобы сумма радиусов вер­шин зубьев соседних сателлитов, равная d_ga = m(z_g + 2), была меньше расстояния l между их осями (см. рис. 2.3), т.е.

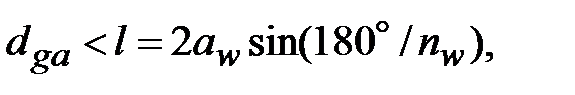(2.6)

где a_w = 0,5sin(z_a + z_g ) – межосевое расстояние.

Из формулы (2.6) следует, что условие соседства выполнено, когда

2.6. Расчет планетарных передач на прочность

Расчет на прочность планетарных передач ведут так же, как для обычных зубчатых передач. Расчет выполняют для каждого за­цепления. В передаче, изображенной на рис. 2.1., необ­ходимо рассчитать внешнее зацепление колес аи gи внутреннее – колес gиb. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление.

При определении допускаемых напряжений [ ]_н, [ ]_f коэф­фициенты долговечности Z _n и Y _n находят по эквивалентным числам циклов нагружения
N_HE = μ_HN_k и N_FE = μ_FN_k соответственно. А числоцикловперемены напряжений зубьев N_k за весь срок службы вычисляют при вращении колес только относительно друг друга.

Для центральной шестерни

где n_w – число сателлитов; L_h – суммарное время работы передачи, ч;

п'_а = (n_a – n_h) –относительная частота вращения центральной шестерни;

п_а и n_h – частоты вращения центральной шестерни и во­дила, мин ^–1.

По п'_а вычисляют окружную скорость, в соответствии с которой назначают степень точности передачи и выбирают коэффициенты К_HV, К_FV .

Для сателлитов N_kg = 60n₃n'_gL_h,

где n₃ – число нагружений зуба за один оборот сателлита;

n'_g = n'_a z_a / z_g – относительная частота вращения сателлита.

Зуб сателлита за один оборот нагружается дважды – в зацепле­ниях с колесами а и b. Однако при определении числа циклов при­нимают п₃= 1, так как при расчете на контактную прочностьучи­тывают, что зуб сателлита работает с колесами аи b разными боко­выми сторонами, а при определении для зубьев сателлита допускае­мых напряжений изгиба[σ]_Fg вводят коэффициент Y_А, учитываю­щий двухстороннее приложение нагрузки (симметричный цикл на­гружения). Значения Y_A принимают:

Y_A =0,65; 0,75; 0,9 соответст­венно для улучшенных, закаленных ТВЧ (или цементованных) и азотированных сталей.

Межосевое расстояниепланетарной прямозубой передачи для пары колес внешнего зацепления (центральной шестерни с сателли­том) определяют по формуле:

где и' = z_g / z_a – передаточное число пары колес; k_w = 1,05 ... 1,15 – коэффициент неравномерности распределения на­грузки между сателлитами; Т₁ = Т_а – вращающий момент на валу цен­тральной шестерни, Н∙м; n_w - число сателлитов; ψ_ba –коэффициент ширины венца колеса.

Ширина b_b центрального колеса b: b_b = ψ_ba a_w. Ширину b_g венца сателлита принимают на 2 ... 4 мм больше значения b_b , цен­тральной шестерни –
b_а = l,1b_g.

Модуль зацепления m = 2a_w/(z_g + z_a).

Полученный расчетом модуль округляют до ближайшего стан­дартного значения, а затем уточняют межосевое расстояние:

a_w = m(z_g +z_a)/2.

Расчет на изгиб выполняют как для обычных зубчатых передач.

Контрольные вопросы

1. Какая зубчатая передача называются планетарной? Какова её конструкция и как она работает?

2. Как получить дифференциальную передачу? Какие возможности предоставляет дифференциальная передача?

3. Каковы основные достоинства и недостатки планетарных
передач по сравнению с обычными зубчатыми?

4. Какой метод используют для опреде­ления передаточного отношения планетарной передачи?

5. Можно ли получить различные значения передаточного отношения планетар­ной передачи в зависимости от остановленного звена?

6. В чем сущность условий соосности, симметричного расположения сателлитов (сборки) и соседства планетарных передач?

На рис. 19.1, а показано относительное расположение недефор-мированного гибкого 1 и жесткого 2 колес. При этом dy < d2;

7. Почему в планетарном редукторе центральную шестерню выполняют ("плавающей")?

8. По какой зависимости определяется передаточное отношение ?

 

 

 

 

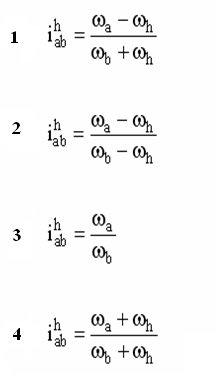
3. ВОЛНОВЫЕ ПЕРЕДАЧИ

 

3.1. Общие сведения

Волновойпередачей называется механизм, содержащий контактирующие между собой гибкое и жесткие звенья и обеспечивающий передачу движения за счет бегущей волновой деформации гибкого звена.

Существуют фрикцион­ные, зубчатые и винтовые волновые передачи. Наиболее распространены зубчатые волновые передачи.

Волновые зубчатые передачи кинематически представляют собой планетарные передачи с одним гибким зубчатым колесом.

Наиболее распространенная волновая передача (рис. 3.1) состоит из водила Н, вращающегося гибкого колеса 1 с наружными зубьями и неподвижного жесткого колеса 2 с внутренними зубьями.

 

А А-А

Рис. 3.1. Волновая передача

 

Водило, являющееся генератором волн, состоит из овального кулачка и специального (гибкого за счет тонкостенных колец) шарикоподшипника. Такой подшипник допускает радиальную деформацию колец, соизмеримую с их толщиной, и обеспечивает передачу вращательного движения при деформированных кольцах. Кулачковый генератор лучше других со­храняет заданную форму деформирования под нагрузкой.

Неподвижное колесо закрепляется в корпусе и представляет собой обычное зубчатое колесо с внутренним зацеплением.

Гибкое зубчатое колесо выполнено в виде стакана с тонкой легко деформирующейся стенкой. В левой части стенки нарезаются зубья, правая часть повторяет форму вала. Длина стакана колеса приблизительно равна его диаметру. Жесткое зубчатое колесо соединено с корпусом. Зубья колес чаще всего эвольвентные.

Делительный диаметр d₁гибкого колеса меньше делительного диаметра d₂ жесткого колеса на величину d₂– d₁ = 2W₀.

Размер овала подшипника качения водила по большой оси больше внутреннего диаметра обода гибкого колеса на величину 2W₀.

При сборке в круглое гибкое колесо вставляют генератор волн, придающий колесу овальную форму (при этом как бы образуются два сателлита, связанные гибкой стенкой стакана), и вводят в зацепление с жест­ким колесом. В направлении большой оси эллипса зацепление зубьев гибкого колеса с зубьями жесткого колеса происходит по всей рабочей высоте зуба, в направлении малой оси эллипса зубья не зацепляются. Происходит это следующим образом: при деформировании гибкого колеса гене­ратором волн зубья гибкого колеса под действием радиальных сил F_r пе­ремещаются по радиусу и входят в зацепление с зубьями жесткого колеса в направлении большой оси эллипса. При переходе от большой оси к малой зубья гибкого колеса вследствие его деформации постепенно пере­мещаются к центру и выходят из зацепления с зубьями жесткого ко­леса. Между этими зонами зубья гибкого колеса погружены во впадины жесткого на разную глубину.

В одновременном зацеплении нахо­дится большое число зубьев: 25–40 % от числа зубьев гибкого ко­леса. Даже при небольшой нагрузке на каждый зуб передача может передавать значительный вращающий момент.

Передача движения в передаче обусловлена, таким образом, деформированием зубчатого венца гибкого колеса: при вращении водила волна деформации бежит по окружности гибкого зубчатого венца и при этом венец обкатывается по неподвижному жесткому колесу в обратном направлении, вращая стакан и вал. Принцип действия определил название передачи – волновая, а водило называют волновым генератором.

При движении водила овальной формы образуются две волны – такая передача называется двухволновой. Существуют также трехволновые передачи (применяют при необходимости большого передаточного отношения. Их недостаток – большие напряжения изгиба в гибком колесе).

Достоинства.

Многопарность зацепления (в зацеплении могут находится до 40 % всех зубьев) определяет положительные качества этих передач:

· большие передаточные отношения в одной ступени: минимальное – 70 (ограничивается изгибной прочностью гибкого зубчатого венца), максимальное – 300…320 (ограничивается минимально допустимой величиной модуля, равной 0,15…0,2 мм). КПД при этом равен 78…85 % (как и в планетарных передачах при тех же передаточных отношениях). В режиме мультипликатора КПД равен 55…65 %;

· способность передавать большие вращающие моменты;

· высокая кинематическая точность передач, плавность работы;

· возможность передавать вращение "через стенку": из герметизированного пространства в вакуум без применения подвижных уплотнений вращающихся деталей (что важно в химической, авиационной промышленности и др.);

· малые нагрузки на валы и опоры за счет симметричности конструкции;

· компактность и малая масса;

· невысокий уровень шума при работе.

К недостаткам волновых передач относят:

· при применении мелких модулей зацепления (0,15…0,2 мм) требуется специальное зубодолбежное оборудование;

· сложность изготовления гибких тонкостенных колес и волнового генератора;

· ограничение частот вращения генератора из-за возникновения вибраций.

Волновые передачи применяют в промышленных роботах и манипуляторах, в механизмах с большим передаточным отношением, а также в устройствах с повышенными требованиями к кинематической точности или к герметичности.

Существует много разновидностей волновых передач (рис. 3.2).

Рис. 3.2. Кинематические схемы некоторых волновых зубчатых передач

На (рис. 3.2, а) изображена передача, в которой закреплено жесткое колесо z₂и вращение передается от h к z₁ .

На (рис. 3.2, б, в) ведущим звеном передач является генератор волн h, ведомым – жесткое колесо z₂ , колесо z₁ неподвижно. Схема (рис. 3.2, в)используется для передачи движения из герметизированного пространства к жесткому колесу z₂ через неподвижное гибкое колесо z₁.

Волновые передачи применяется в космической и вакуумной технике в качестве редукторов, дифференциалов и вариаторов скорости.

Передачу с коротким гибким колесом (рис. 3.2, г) чаще используют при z_1м = z_2м= z₁, используя зацепление z_1м = z_2м как подвижное шлицевое соединение. Передаточные отношения передач для схем на рис. 2.2, а, б, в лежат в пределах 70 ≤ и≤ 320, КПД в пределах от 0,75 до 0,85. Передаточное отношение передачи для схемы на рис. 3.2, г лежит в пределах от 0,7 до 0,8.

 

3.2. Принцип работы волновой зубчатой передачи

Работу волновой зубчатой передачи можно рассмотреть, исследуя силовое взаимодействие звеньев (рис. 3.3).

 

 

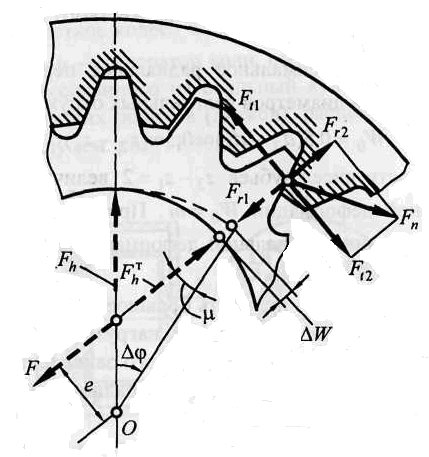
Рис. 3.3. Принцип действия волновой зубчатой передачи

После сборки передачи результирующий вектор деформации F_h действует на гибкое колесо по большой оси генератора волн. При повороте генератора волн по часовой стрелке на бесконечно малый угол ∆φ вектор результирующих сил поворачивается в ту же сторон, увеличиваясь по модулю . Зубья гибкого колеса, перемещаясь в радиальном направлении на величину ∆W, давят на зубья жесткого колеса с силой F_n по нормали к их профилю. Эта сила раскладывается на окружную F_t2 и радиальную F_r2. На зуб гибкого колеса действует такая же система сил, но в обратном направлении. Если закреплено жесткое колесо, то под действием сил F_t1 жесткое колесо вращается в сторону, обратную вращению генератора волн. Если закреплено дно гибкого колеса, то под действием сил F_t2 жесткое колесо вращается в сторону вращения генератора волн.

Возможна работа передачи в режиме мультипликатора (ускорителя); рассмотрим этот режим, когда закреплено дно гибкого колеса.

При вращении жесткого колеса против часовой стрелки возникает приведенная выше система сил в зацеплении.

На генератор волн в точке контакта по нормали к профилю кулачка давит сила F ≈ F_r2 с плечом е относительно оси вращения О. Момент F ∙е вращает генератор волн, если угол μ будет больше угла трения. Если в генераторе установить подшипники скольжения, то передача будет самотормозящей. График перемещений W напоминает волновую функцию. На углу 2π отложены две волны деформации, поэтому передачу называют двухволновой. При вращении генератора волна катится (перемещается, бежит) вдоль оси абсцисс (по окружности гибкого колеса).

3.3. Передаточное отношение зубчатой волновой передачи

В волновой передаче (как и в планетарной) каждый из трех основных элементов может быть ведущим (воспринимать внешние моменты). Любое основное зве­но может быть остановлено.

1. Остановлен генератор(ω_h = 0). Вращение передается от гибкого колеса с числом зубьев z₁к жесткому (z₂) – обычное внут­реннее зацепление:

.

В формуле знак плюс, так как направления вращения ω₁ и ω₂ совпадают.

2. Остановлено жесткое колесо(ω₂ = 0). Это наиболее частый случай (обычная волновая передача).

Рассмотрим дифференциальную волновую передачу со всеми тремя подвижными звеньями, имеющими угловые скорости ω₁, ω₂, ω_h .

Выберем систему координат, неподвижно связанную с генера­тором. Для этого мысленно зададим всей системе угловую скорость (-ω_h). Тогда звенья будут иметь относительные угловые скорости:

т.е. относительно неподвижного генератора оба колеса будут казать­ся вращающимися.

Тогда, как и в первом случае, можем записать

.

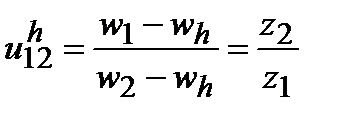Если остановлено жесткое колесо, то движение передается от генератора к гибкому колесу, и, следовательно, нужно найти

 

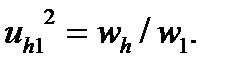
Полагая в формуле для дифференциальной передачи ω₂ = 0, имеем