Расчет зубьев цилиндрической прямозубой передачи на изгиб

2015-12-06

2248

Обсуждений (0)

0.00 из 5.00 0 оценок

⇐ Предыдущая 9 10 11 12 131415 16 17 18 Следующая ⇒

3.33. Ниже излагается упрощенный метод расчета зуба на изгиб, основанный на положениях сопротивления материалов.

На рис. 3.34 показаны схема зацепления двух зубьев в полюсе и силы, действующие на зубья колес со стороны шестерни; трение не учитывается. Нормальная сила F_n раскладывается на две составляющие: окружную силу F_t и радиальную или распорную — F_r.

Рис. 3.34. Усилия-в зацеплении прямозубой цилиндрической передачи

При выводе формул принимают следующие упрощения и допущения: зуб рассматривают как консольную балку прямоугольного сечения, работающую на изгиб и сжатие; вся нагрузка, действующая в зацеплении, передается одной парой зубьев и приложена к их вершинам; нагрузка равномерно распределена по длине зуба Ь_ω.

На рис. 3.35 показан профиль балки равного сопротивления (s — толщина зуба в опасном сечении; l — плечо изгибающей силы; b_w — длина зуба; F_n — нормальная сила, действующая на зуб).

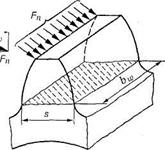
Рис. 3.35. Схема расчета зубьев на изгиб

Определим силы в опасном сечении корня зуба. Разложим силу F_n в точке А на две составляющие: F,' и F'_r, условно принимаем, что сила F_n приложена только к одному зубу (перекрытием пренебрегаем), а сила F, равна окружной силе на начальной окружности.

Сила F_t^/ изгибает зуб, а сила F'_r сжимает его. Из рис. 3.35 находим

F_t' = F_ncosa'; F'_r = F_n sin α'

где α' — угол направления нормальной силы F_n, приложенной у вершины, который несколько больше угла зацепления a_ω; F_n – F_t /cos a_w — нормальная сила.

В каком сечении зуба рис. 3.35 возникает наибольшая концентрация напряжений?

3.34.Исходя из изложенного выше, за расчетное напряжение принимают напряжения на растянутой стороне зуба:

(3.1)

Для опасного сечения ВС условие прочности

(3.2)

где a_F — напряжение изгиба в опасном сечении корня зуба; W — осевой момент сопротивления; А = b_ωs — площадь сечения ножки зуба.

Выразим I и s в долях модуля зубьев: l= km; s = cm, где к и с — коэффициенты, зависящие от формы зуба, т. е. от угла а_ω и числа зубьев Z.

Тогда изгибающий момент в опасном сечении

осевой момент сопротивления прямоугольного сечения зуба

(3.3)

Подставим в формулу (3.2) входящие в него параметры М_И и W, введем коэффициенты расчетной нагрузки K_Fβ (табл. 3.4), K_Fv (табл. 3.5) и теоретический коэффициент концентрации напряжений К_Т.

В результате получим окончательную формулу проверочного расчета прямозубой передачи на усталость при изгибе

(3.4)

где Y_F — коэффициент учитывающий форму зуба и концентрацию напряжений (табл. 3.6).

Таблица 3.4. Значение коэффициентов K_Fβ и K_Hβ

! Расположение шестерни относительно опор Твердость НВ поверхностей зубьев колеса K_Fβ при Ψbd=^bw/d₁ К_Hβ при Ψbd =b_ω/d₁

0,2 0,4 0,6 0,8 1,2 1,6 0,2 0,4 0,6 0,8 1,2 1,6

Консольное (опоры — шарикоподшипники) До 350 Св. 350 1,16 1,33 1,37 1,70 1,64 1,08 1,22 1,17 1,44 1,28

Консольное (опоры — роликоподшипники) До 350 Св. 350 1,10 1,20 1,22 1,44 1,38 1,71 1,57 1,06 1,11 1,12 1,25 1,19 1,45 1,27 -

Симметричное До 350 Св. 350 1,01 1,02 1,03 1,04 1,05 1,08 1,07 1,14 1,14 1,30 1,26 1,01 1,01 1,02 1,02 1,03 1,04 1,04 1,07 1,07 1,16 1,10 1,26

Несимметричное До 350 Св. 350 1,05 1,09 1,10 1,18 1,17 1,30 1,25 1,43 1,42 1,73 1,61 1,03 1,06 1,05 1,12 1,07 1,20 1,12 1,29 1,19 1,48 1,28 -

Таблица 3.5. Значение коэффициентов K_Fv и K_HV

Степень точности передачи Твердость НВ поверхности зубьев колеса K_Fv (A/fo) при окружной скорости, м/с

До 350 Св. 350 1,08/1,03 (1,04/1,02) 1,03/1,01 (1,03/1,00) 1,16/1,06 (1,07/1,03) 1,05/1,02 (1,05/1,01) 1,33/1,11 (1,14/1,05) 1,09/1,03 (1,09/1,02) 1,50/1,16 (1,21/1,06) 1,13/1,05 (1,14/1,03) 1,62/1,22 (1,29/1,07) 1,17/1,07 (1,19/1,03) 1,80/1,27 (1,36/1,08) 1,22/1,08 (1,24/1,04)

До 350 Св. 350 1,10/1,03 (1,04/1,01) 1,04/1,01 (1,03/1,01) 1,20/1,06 (1,08/1,02) 1,06/1,02 (1,06/1,01) 1,38/1,11 (1,61/1,04) 1,12/1,03 (1,10/1,02) 1,58/1,17 (1,24/1,06) 1,16/1,05 (1,16/1,03) 1,78/1,23 (1,32/1,07) 1,21/1,05 (1,22/1,04) 1,96/1,29 (1,40/1,08) 1,26/1,08 (1,26/1,05)

До 350 Св. 350 1,13/1,04 (1,05/1,01) 1,04/1,01 (1,04/1,01) 1,28/1,07 (1,10/1,03) 1,07/1,02 (1,07/1,01) 1,50/1,14 (1,20/1,05) 1,14/1,04 (1,13/1,02) 1,72/1,21 (1,30/1,07) 1,21/1,06 (1,20/1,03) 1,98/1,28 (1,40/1,09) 1,27/1,08 (1,26/1,04) 2,25/1,35 (1,50/1,12) 1,34/1,09 (1,32/1,05)

Примечание. В числителе — значения для прямозубых колес, в знаменателе — для косозубых.

Таблица 3.6. Коэффициент Y_F -для эвольвентного наружного зацепления приa_w = 20° (прих = О)¹

Число зубьев Yf Число зубьев Y_F Число зубьев Y_F

4,26 3,81 3,62

4,07 3,79 3,60

3,98 3,75 3,60

3,92 3,70 3,60

3,88 3,66 3,60

3,65 Рейка 3,63

¹Выбор коэффициента Y_F можно производить по графику.

Как определяются в формуле (3.4) коэффициенты К_Fβ, K_FV, Y_F?

3.35.Выведем формулу проверочного расчета прямозубых передач на усталость при изгибе через вращающий момент Т₂..

С учетом того, что F_t= 2T₁/d₁ = 2T₁/ mz₁ = 2T₂/mz₁u; b_ω = Ψ_bdmz₁формула проверочного расчета (3.4) примет вид

(3.5)

где σ_F, [σ]_F, МПа; m, мм; T₂ — вращающий момент на колесе, Н · мм; Z₁ — число зубьев шестерни; Ψ_bd — коэффициент длины зуба (ширины венца) по делительному диаметру (табл. 3.7).

Таблица 3.7. Рекомендуемые значения коэффициента Ψ_bd = b_w/d₁ в зависимости от твердости рабочих поверхностей зубьев

Расположение колес относительно опор НВ₂ ≤ 350 или НВ₁ и НВ₂ ≤ 350 НВ₁ и НВ₂ > 350

Симметричное 0,8-1,4 0,4-0,9

Несимметричное 0,6-1,2 0,3-0,6

Консольное 0,3-0,4 0,2-0,25

3.36. В каком случае проводят проверочный расчет зубчатой передачи на изгиб?

3.37. Проанализируйте формулы (3.5) и определите, в каких зубьях (шестерни или колеса) возникают большие изгибающие напряжения и почему?

3.38.Из формул (3.5) и (3.6) получаем формулы проектировочного расчета на изгиб

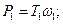(3.6)

(3.7)

(3.8)

где K_m = 1,4 для прямозубых колес.

В формулу (3.8) подставляют меньшее из двух отношений [σ]_F/Y_F, вычисленных для шестерни и колеса.

В каких единицах необходимо подставить T₂и [σ]_F в формулу(3.8), чтобы модуль т получить в миллиметрах.

3.39. Выбор допускаемых напряжений изгиба. Выше отмечалось, что причиной поломки зубьев, как правило, является усталость материала под действием повторных переменных изгибающих напряжений. Поэтому значения допускаемых напряжений должны быть определены исходя из предела выносливости зубьев. Допускаемое напряжение изгиба определяют по формуле

[σ]_F=(σ⁰_Flimb/S_F)Y_RK_FCK_FL, (3.9)

где σ⁰_Flimb — базовый предел выносливости зубьев при отнулевом цикле изменения напряжений (табл. 3.8); S_F — коэффициент безопасности (S_F = 1,7 ÷ 2,2; S_F> 2,2 — для литых заготовок); Y_R — коэффициент, учитывающий шероховатость поверхности зуба (Y_R= 1,05 -г 1,2 — при полировании, в остальных случаях Y_R= 1); K_FC — коэффициент, учитывающий влияние двустороннего приложения нагрузки (K_FC= 1,0 — при одностороннем приложении нагрузки, изгибающей зуб; K_FC= 0,65 — для нормализованных сталей, K_FC=0,75 — для закаленных сталей с твердостью свыше HRC45; K_FC = 0,9 — для азотированных сталей); K_FL — коэффициент долговечности [определяется по формуле (ЗЛО, 3.11)].

Таблица 3.8. Приближенные значения пределов выносливости при изгибе зубьевσ⁰_Flimb

σ⁰_Flimb. МПа Твердость зубьев HR С Сталь Способ термической или химико-термической обработки

Поверхность Сердцевина

1,8HB_СР НВ 180-300 Углеродистая или ле_гтированная Отжиг, нормализация или улучшение

550-600 HRC 45-55 Легированная Объемная закалка

750-850 48-58 30-45 Поверхностная закалка

750-850 56-62 32-45 Цементация и нит-роцементация

300 + \,2HRC (сердцевины зуба) 50-60 24—40 Азотирование

Можно ли принимать при расчете модуля т прямозубой передачи значения прочностных характеристик материала зубчатых колес из табл. 3.8 для подстановки в формулу (3.8)?

3.40.В зависимости от твердости активных поверхностей зубьев коэффициент долговечности Y_N определяется по следующим формулам:

K_FL = при НВ≤ 350, (3.10)

K_FL = при НВ ≥ 350, (3.11)

где N_F₀ = 4 · 10⁶ — число циклов соответствующее точке перелома кривой усталости; N_F — расчетная циклическая долговечность;

N_F= 60nct_π = 573ωct_∑, (3.12)

где n(ω) — частота вращения (угловая скорость) шестерни или колеса, об/мин (рад/с); с — число колес, находящихся в зацеплении с рассчитываемым колесом; t_∑ — продолжительность работы зубчатой передачи за расчетный срок службы, ч;

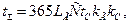(3.13)

где L_Г — срок службы передачи, год; С — число смен; t_c — продолжительность смены, ч; k_Г — коэффициент годового использования привода; k_с — коэффициент использования привода в смене.

Формула (3.12) приемлема для определения расчетной циклической долговечности только при постоянном режиме нагрузки.

При выборе материала для зубчатой пары с целью сокращения номенклатуры, как правило, назначают одинаковые материалы. Разность значений твердостей для шестерни и колеса достигается их термической обработкой. Получение нужных механических характеристик зависит не только от температурного режима обработки, но и от размеров заготовки.

3.41.При переменном режиме нагрузки расчетная циклическая долговечность определяется по формуле:

N_F=60·n·c·t_∑K_FE, (3.14)

где K_FE — коэффициент приведения переменного режима нагрузки к постоянному эквивалентному режиму:

(3.15)

где T_max, Т_i — максимальные и промежуточные значения моментов; коэффициент m_F = 6 — при нормализации и улучшении; m_F=9 — при закалке; t_i — продолжительность (в часах) действия момента Т_i,; t_∑ — суммарная продолжительность работы зубчатой передачи.

3.42.Ответить на вопросы контрольной карточки 3.6.

Контрольная карточка 3.6

Вопрос Ответы Код

По какой формуле производят проектировочный расчет прямозубой передачи на изгиб?

Как называется коэффициент, обозначаемый буквой K_β? Формы зуба Длина зуба Расчетной нагрузки Концентрации напряжений

Определите коэффициент формы зуба колеса, если zz = 150; и = 4 4,26 3,79 3,60 3,63

В каких размерных единицах подставляют модуль зацепления в формулу (3.7) для определения a_F? мм см м Величина безразмерная

По какой формуле определяют допускаемое напряжение изгиба при одностороннем направлении вращения ведущего вала?