Вариационные параметризации и регуляризация

Методы регуляризации, к числу которых относятся и методы квазирешений, развиты в предположении, что не выполнены первое и третье условие корректности. Это означает, что если решение существует, то оно единственно. Рассмотрим, связь между результатами решения обратной задачи методами регуляризации и вариационной параметризацией в форме (17) без предположения однозначной разрешимости уравнения (16).

Постановка обратной задачи в методах регуляризации А.Н. Тихонова выглядит так:

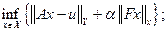(5.21)

. (5.22)

Здесь Х, Y- соответствующие банаховы пространства, F - линейный оператор (см. 4.3.). Предположим, что нижние грани в приводимых задачах достигаются, и есть (для каждой из задач этот элемент свой). Легко убедиться в том, что найденный таким образом элемент принадлежит экстремальному классу 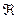, порожденному задачей

при 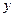, пробегающим все . Действительно, если есть решение какой-либо из задач (21) или (22) и , то есть и решение задачи:

В противном случае нижняя грань в (21) либо (22) достигалась бы на другом элементе. Однако в (21) или (22) компоненты задачи - Х,Y, F выбираются так, чтобы обеспечить устойчивость решения, которое теоретически единственно. Именно свойства устойчивости, а не единственности отражены в конструкциях Х,Y, F. Использование этих компонент одновременно и для отбора единственного решения из класса эквивалентных смешивает эти понятия, является противоестественным и, не позволяя целенаправленно использовать информацию для обеспечения единственности решения, ведет к построению формально эквивалентных, а не содержательных моделей. Отбор единственного из множества формально эквивалентных требует своих, иных принципов, которые нельзя смешить с принципами для обеспечения устойчивости. В основе критериального подхода формирования классов единственности – вариационной параметризации, единственность решение обеспечивает требование минимума функционала . Этот функционал (включающий в себя параметры Х,F, конкретизирующие его вид ) должен выбираться как выражение априорной информации о свойствах решения, позволяющей осуществить его отбор решения в классе себе эквивалентных. Его назначение – построить экстремальный класс единственности 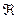. Лишь после того, как этот класс построен, можно использовать методы теории регуляризации для устойчивого нахождения элемента 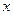из 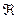, соответствующего заданному полю. Ясно, что такой подход является преимущественным, поскольку учитывает специфику обратных задач, имеющих неединственное решение. Он позволяет разделить критерии для формирования свойств единственности и устойчивости, не путая эти свойства. Этот подход позволяет сформировать классы единственности, соответствующие заданному принципу оптимальности, а для устойчивого нахождение решения в этом классе использовать свой критерий, несущий информации о требуемых характеристиках устойчивости.

Напомним результаты рассмотрений, приведенных в п.3.2. и 4.4. в связи с изучением свойств квазирешений. Там было показано, что если М – линейное пространство, и А – линейный ограниченный оператор, то квазирешение 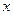задачи , полученное градиентными средствами минимизации определено условием:

,

где - принятое нулевое приближение. Но это условие представляет собой необходимое и достаточное условие того, что квазирешение есть решение задачи:

при некотором (доказательство см. ниже). Таким образом, построение квазирешения на линейном подпространстве М эквивалентно построению ближайшего из класса эквивалентности, соответствующего заданному полую элемента, к принятому нулевому приближению 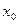в норме пространства . Реализуется принцип построения ближайшего к нулевому приближению в квадратичной метрике. И это решение суть гармоническая функция. Следовательно, рассматривая обратные задачи в условиях эквивалентности - имеющие, вообще говоря, неединственное решение, мы, так либо иначе, вводим принципы оптимальности. Но эти принципы фигурируют неявным образом, они заложены в алгоритме получения решения. На примере задачи гравиметрии в предыдущем разделе показаны их «экзотические» свойства. Поэтому в условиях эквивалентности, для получения содержательных решений, более оправданным является применение методов, позволяющих управлять этими принципами, используя их в активной форме.

 

 

5.2.3. Квадратичные критерии оптимальности[20].

 

Еще раз покажем, что использование критериев оптимальности – естественный язык выражения априорной информации об изучаемой модели среды. Для иллюстрации этого следует, прежде всего, определиться с термином “априорная информация”. Дать ему полное определение весьма затруднительно. Лучше всего охарактеризовать некоторые, наиболее явные свойства априорной информации. Самое главное ее свойство состоит в том, что, она характеризуется неопределенностью, не позволяющей однозначно найти параметры изучаемого объекта (в противном случае обратная задача была бы тривиальной). Но неопределенность эта такова, что позволяет на множестве всех допустимых возможных распределений физического параметра установить отношение частичного упорядочения по степени соответствия того либо иного элемента имеющейся априорной информации. Это означает, что для любых двух допустимых элементов можно указать, какой из них более, а какой менее согласуется с априорной информацией, либо они ей соответствуют в одинаковой степени. Если теперь этому отношению порядка поставить в соответствие отношение порядка на вещественной прямой, то получим функционал на множестве Х, обладающий тем свойством, что он принимает на элементе 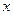тем большее значение, чем в большей мере элемент 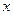соответствует имеющимся априорным данным. Таким образом, формулировка обратной задачи как выделения из класса эквивалентности элемента, максимизирующего этот функционал, оказывается естественной. В большинстве интересных для приложений случаев задачу на максимум можно свести к задаче на минимум, и именно так в дальнейшем и будем поступать.

Рассмотрим некоторые примеры. Первый из них повторяет и распространяет на более общий случай рассуждения, приведенные выше в связи с введением критериев для структурной задачи гравиметрии.

Предположим, что имеется некоторое нулевое приближение к искомому распределению физического параметра в среде. Символ v означает точку области V пространства, в которой изучается физическая модель среды. Среди всех элементов из класса эквивалентности, соответствующего заданной наблюдаемой, следует найти ближайший к в норме пространства Х, например, в смысле наименьших квадратов. Это приводит к функционалу:

 

.

(4.23)

 

Если дополнительно потребовать, чтобы не только , но и его производные до порядка были близки к соответствующим компонентам нулевого приближения, получим критерий оптимальности:

.

(5.24)

Более сложный и интересный для приложений пример таков.

Нулевое приближение , которое является, как правило, обязательной компонентной априорной информации, строится на основании комплекса разнородной геолого-геофизической информации. Разные компоненты этого комплекса, равно как и различные составляющие одной и той же компоненты, но относящиеся к различным по сложности строения участкам среды, различаются между собой по точности построения. Причем, эта точность может быть оценена в терминах априорной оценки среднеквадратичной погрешности построения различных компонент нулевого приближения . Именно эти две составляющие - нулевое приближение и дифференцированная оценка точности его построения, в большей мере выражают объективную дополнительную информацию о , чем только принятие нулевого приближения. Приняв, что в точке уклонение нулевого приближения от истинного распределения искомого физического параметра можно рассматривать как одну реализацию нормально распределенной случайной величины с нулевым средним и оценкой стандарта , и воспользовавшись хорошо известным приемом перехода к функции правдоподобия (см. пример п.5.1), получаем критерий для максимизации правдоподобия встречи распределения (с точки зрения компонент и ):

(5.25)

Проиллюстрируем этот прием.

Пусть модель среды параметризирована вектором , и есть нулевое приближение к , а - оценка среднеквадратичной погрешности построения нулевого приближения. Точнее 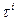оценивает среднеквадратичную погрешность построения .

Следовательно, величину ( ) можно считать распределенной по нормальному закону с нулевыми средним и среднеквадратичным уклонением 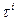. тогда для любого значения вероятность его наблюдения рассчитывается по формуле:

.

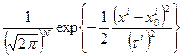Считая, что все компоненты вектора как случайные величины являются независимыми[21], получаем, что вероятность наблюдения вектора рассчитывается по формуле:

. (5.25-a)

Эта функция называется функцией правдоподобия для вектора . Чем больше значение функции правдоподобия на том либо ином элементе, тем более вероятно именно это значение компонент вектора . Следовательно, необходимо максимизировать функцию правдоподобия, и это обеспечит учет априорной информации о распределении значений компонент вектора . Нетрудно заметить, что ее максимизация эквивалентна минимизации функционала:

. (5.26)

Нетрудно заметить, что выражения (24),(25),(26) можно записать в единой форме:

, (5.27)

где – некоторый линейный оператор, а Х – функциональное пространство. Компоненты Х (вид нормы) и вид оператора в функционале (27) не являются независимыми. В обозримых для приложения случаях можно считать, что всегда найдется такой замкнутый оператор 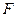, что минимизация (27) эквивалентна минимизации функционала:

.

(27а)

Например, (24) сводится к предыдущему выражению, если F - оператор дифференцирования.

В примере (25) F- это оператор умножения на весовую функцию и . В примере (26): F- покомпонентное умножение на весовые множители , а . В примере (24) , а

Замена переменных сводит задачу (27) к виду (с целью единообразия в (27) используем запись с . Это всего лишь вопрос обозначений):

(5.28)

Задача (28) является главной для последующих рассмотрений. Основным является случай (Х=С рассматривается особо). Критерии оптимальности (26) и (27) при 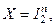эквивалентны, поскольку сводятся друг к другу надлежащей заменой переменного. Действительно, далее будет показано, что решение задачи (28) (для случаев 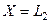) имеет вид:

. (5.28¹)

Оператор - самосопряженный, положительный и, следовательно, имеет положительный и самосопряженный корень[22] (который может и не совпадать с F). Тогда влияние на результат решения задачи (28) при 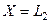операторов F или одинаково. Следовательно, введение критериев оптимальности:

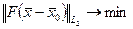; (5.28²)

, (5.28³)

приводит к одному и тому же результату. В силу свойств оператора F (это матрица размерности 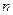) он может быть приведен к диагональному виду (прил.1), и, следовательно, линейной заменой переменных (разложение по собственным векторам) задача (28) с критерием (28³) сводится к той же задаче с критерием (26), где величины связаны с собственными значениями оператора F. Преобразование параметров такое, что критерий оптимальности (28³) приводится к диагональному виду (26), переводит вектор в новый вектор . для последнего также может быть сконструирован оператор решения прямой задачи и, тем самым, общая задача (28) при 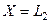сводится к той же задаче с критерием (26).

Для формирования критерия оптимальности более удобна форма (26), поскольку коэффициенты имеют простой физический смысл: - априорная оценка погрешности построения i-ой компоненты нулевого приближения. Однако и матрица F может формироваться из простых физических соображений, сходных с теми, что использовались для выбора коэффициентов , но несколько более общих.

Действительно, выражение (25-а) для функции правдоподобия (исходя из которой и было найдено выражение (26)) получено, исходя из гипотезы о нормальном распределении ошибок (распределение Гаусса) и независимости компонент и при . Последнее условие может быть ослаблено, если допустить (в рамках того же нормально закона) зависимость параметров модели. В этом случае необходимо дать априорную оценку степени зависимости компонент и . Последняя будет полностью определена, если задать матрицу моментов (ковариационную матрицу):

где М - знак вычисления математического ожидания. Величины 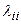оказываются оценками дисперсий компонент . Функция правдоподобия для вектора будет иметь вид:

,

где - матрица, обратная к , - определитель матрицы . Максимизация записанной функции правдоподобия эквивалентна минимизации формы:

.

поскольку Λ- симметричная и положительно определенная матрица (что следует из аналогичных свойств матрицы моментов ), то существует ее квадратичный корень, также положительный и симметричный. Следовательно:

где Λ^1/2 - квадратичный корень матрицы Λ. Таким образом, мы приходим к критерию оптимальности:

, (5.28⁴)

аналогичному по своей форме критерию (28³). Далее можно применить уже использовавшиеся ранее рассуждения о приводимости критерия (28⁴) к квадратичному виду.

На самом деле знание матрицы Λ^1/2 или Λ не нужно. Достаточно знать матрицу элементов , поскольку решение задачи:

имеет вид:

.

Далее Λ^*1/2 =Λ^1/2 и Λ^1/2 Λ^1/2=Λ и, следовательно:

.

Приведенное обобщение может оказаться полезным при решении не слишком многоразмерных задач. Практически, наиболее распространенной задачей является:

Таким образом, во многих случаях поиск оптимального элемента сводится к поиску наименее уклоняющегося от нуля в том либо ином смысле решения обратной задачи или, что тоже самое, к задаче аппроксимации нуля на классе эквивалентности. При выборе оператора F и функционального пространства Х следует учесть, описанные выше эффекты, связанные с наследованием специальных аналитических свойств решений при единичном критерии. Особо рельефно это было продемонстрировано на примере обратной задачи гравиметрии в классе распределений плотности. Прямой ввод весовой функции как оценки погрешности построения нулевого приближения, неявным образом предполагает равноценность уклонения от нуля величины при . Действительно, говоря о том, что оценивает среднеквадратичное уклонение от нуля величины , мы не явно предполагаем, что при величина будет уклоняться от нуля равномерно во всех точках не в формально математическом, а в некотором интуитивно предполагаем смысле. В то же время, на самом деле при , может вести себя самым “причудливым” образом. Так в обратной задаче гравиметрии, когда - это распределение плотности, случаю соответствует гармоническая функция, имеющая максимальные и минимальные свои значения на границе области V. В то же время, от требований минимальности уклонения квадратов, интуитивно ожидается некоторое равно небольшое уклонение распределения плотности от принятого нулевого приближения. Учесть такие специфические эффекты можно, например, следующим нестрогим способом.

Пусть случаю соответствует решение , а случаю . Чтобы использование весовой функции приводило к результатам в решении соответствующим тому смыслу, которые закладываются в , необходимо, чтобы , где - ориентировочная пропорциональность. Тогда в качестве можно принять . Иными словами, если - оценка уклонения от нуля искомого решения, то для получения решения, соответствующего этой оценке, следует выбрать весовой множитель в (25): .

Приведенные выше рассмотрения приобретают конкретный и точный смысл в конкретных задачах, поэтому их более подробное рассмотрение должно быть осуществлено при решении конкретных задач.

Дополнительной к приведенной компонентной информации об искомом решении является наличие совокупности ограничения на распределении искомого параметра. Эти ограничения определяют некоторый класс М, которому должно принадлежать искомое распределение. К ним относятся, например, следующие:

, (5.29)

где и - заданные функции. Либо , где С – заданное множество. Например, если ищется распределение плотности в нижнем полупространстве, то в качестве М выступает множество таких распределений плотности, которые принимает только заданный, дискретный ряд значений . Для учета такого рода компонент априорной информации вводится функционал:

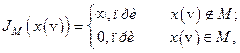
(5.30)

и критерий оптимальности для выделения элемента из класса эквивалентности имеет вид

(5.31)

Поскольку из физических соображений следует, что нулевое приближение априорно удовлетворяет вводимым ограничениям на искомое распределение, то , и можно выполнить замену переменных:

.

Критерий оптимальности перепишем в в виде:

, (5.32)

Где .

Функционал (31) является достаточно общим, поскольку структура множества М может быть весьма разнообразной.

 

5.3. Экстремальные классы единственности для интегральных критериев оптимальности.

 

Пусть - линейные операторы, действующие из банахова пространства 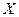в банаховы пространства соответственно (в частном случае пространства 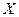и могут совпадать).

Определение 1. Экстремальным классом называется совокупность решений задачи:

(5.33)

при 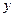, пробегающим все .

Существование решение в (33) не предполагается. Поэтому для некоторых в множестве может не существовать соответствующих элементов. Кроме того, поскольку (33) в общем случае имеет неединственное решение, то между и , вообще говоря, нет взаимно-однозначного соответствия.

Определение 2. Если М – множество в D(A) такое, что для всех на М существует решение уравнения

(5.34)

 

то М называется полным классом. Полный класс единственности для уравнения (34) называется идеальным классом. Если М – класс единственности, и для любых и существует решение неравенства:

(5.35)

то М называется почти идеальным классом.

Ясно, что всякий идеальный класс есть одновременно и почти идеальный. С другой стороны, если оператор А непрерывен, M – идеальный класс, а G – плотное в подмножество, то G – почти идеален.

Понятие идеального и почти идеального класса важны с той точки зрения, что характеризуют интерпретационные возможности метода решения обратной задачи, использующего этот класс в качестве модельного. Если класс неполон, то метод решения обратной задачи не использует всей информации заложенной в наблюдаемой Идеальные классы наиболее полно сочетают в себе максимальное использование всей информации заложенной в наблюдаемой – и одновременно возможность реконструкции модели единственным образом. Для идеальных классов решение обратной задачи единственно и для каждой наблюдаемой может быть получено теоретически абсолютно точно. Для почти идеального класса – единственно, но лишь с любой наперед заданной точностью. Свойства решения на идеальных или почти идеальных экстремальных классах регулируются параметрами критерия оптимальности, выражающего экстремальный принцип.

Теорема 1. Пусть Z – равномерно выпуклое банахово пространство, А – линеен и ограничен из X в Y, и: KerF KerA = 0; F – ограничен и имеет ограниченный обратный. Тогда – идеальный экстремальный класс.

Доказательство. В силу линейности и ограниченности A на X, KerA есть замкнутое подпространство в X. Таково же будет и множество , как сдвиг KerA. Поскольку F – линеен и взаимно непрерывен из X в Z, то образ при отображении F – множество F( ) есть также замкнутое пространство в Z. Тогда F( ) есть сдвиг F(KerA) и решение задачи:

существует и единственно. Обозначим это решение . Тогда элементу соответствует множество , и на этом множестве решение задачи существует (поскольку содержит хотя бы один элемент из и единственно, поскольку

KerF KerA = 0.

Теорема 2. Пусть А – линейный ограниченный оператор из X в Y, и область определения плотна в Y. F – линейный геоморфизм из X в , 1<p< . Тогда совокупность x, являющихся решением задач

, (5.36)

где , есть идеальный экстремальный класс. Доказать следует, что состоит из всевозможных решений уравнения (36). Рассмотрим задачу:

(5.37)

Ее решение существует и единственно. Точно также существует и единственное решение задачи:

(5.38)

и .

Из теоремы двойственности следуют необходимые и достаточные условия, характеризующие решение (38): в , при 1/q+1/p=1 существует элемент f и

a)

б) ;

в)

Условия (а) и (б) будут выполнены, если в качестве выбрать:

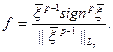
действительно, (а) выполнено, если .

Но:

 

 

Поскольку q=p/(p-1), то:

Далее:

Из условия (в) следует:

откуда:

.

Поскольку все приводимые условия являются необходимыми и достаточными, то этим и завершается доказательство.

Наиболее важный для приложений случай, это – p=2. Экстремальный класс имеет представление:

(5.39)

или:

и является линейным подпространством в X. Этим определяется его конструктивный аспект – на линейном пространстве строить решения линейных задач значительно проще, чем на каком либо ином множестве. Множество , имеющее представление:

(5.40)

где есть плотное в подмножество, и поэтому является почти идеальным экстремальным классом. В дальнейшем для почти идеальных экстремальных классов используется символ .

Если линейный замкнутый оператор F не является геоморфизмом, но ImF и DF плотны в Z и X, соответственно, и, либо F, либо 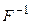ограничены, а KerF=0, то совокупность элементов x, удовлетворяющих одному из уравнений:

(5.41)

или

(5.42)

в предположении образует почти идеальный экстремальный класс .

Покажем это на примере представления (41). Разобьем доказательство на две части.

1) Класс (41) есть класс единственности.

Действительно, рассмотрим уравнение:

(5.43)

Поскольку из него следует то для решения из теоремы о ядре имеем:

Тогда:

Последнее, в силу плотности области определения оператора возможно лишь при Единственность доказана.

2)Уравнение на плотно разрешимо.

Действительно, рассмотрим задачу:

(5.44)

Как известно (см. прил. 2) уравнение плотно разрешимо, если сопряженное к нему уравнение однозначно разрешимо. Но сопряженный к (44) оператор имеет тот же вид: Его однозначная разрешимость показана выше, на предыдущем шаге.

Рассмотрим задачу:

(5.45)

Элемент , удовлетворяющий уравнению2