Определенный интеграл

Пусть функция непрерывна на отрезке . Разобьем отрезок на отрезков точками таких, что Множество точек называют разбиением отрезка ; Обозначим ,, , , - диаметр разбиения . Очевидно, что зависит от . Это записывают так: . Выберем на

каждом отрезке по одной точке , где . Точки называют промежуточными точками. Обозначим множество промежуточных точек буквой .

Обозначим .

Величина называется интегральной суммой функции , соответствующей данному разбиению и промежуточным точкам . Каждое слагаемое интегральной суммы представляет собой площадь прямоугольника, которая приблизительно равна площади криволинейной трапеции ABCD. Поэтому вся сумма дает приближенное выражение для площади криволинейной трапеции, ограниченной графиком функции и прямыми , , (в случае, когда ). Очевидно, что это приближение тем точнее, чем мельче разбиение , то есть чем меньше диаметр разбиения .

Определение 1.Число I называют пределом интегральных сумм при и при этом пишут

I или 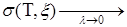I , (10)

если разбиение такое, что для любого выбора промежуточных точек имеет место неравенство .

Замечание 1. В курсе математического анализа доказывается существование предела (10), если функция непрерывна на отрезке .

Определение 2.Предел при интегральных сумм I называется определенным интегралом Римана от функции на отрезке и обозначается . Числа a и b называют нижним и верхним пределом интегрирования соответственно.

Непосредственно из определения выводятся следующие свойства определенного интеграла:

1.

2.

3.

4. .

(Во всех формулах и непрерывны на .)

Связь определенного и неопределенного интегралов задается формулой Ньютона-Лейбница:

,

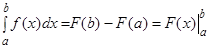где есть первообразная функции , непрерывной на отрезке .

Отметим, что первообразная может быть найдена с помощью вычисления неопределенного интеграла. В курсе математического анализа доказано, что непрерывная на отрезке [a,b] функция имеет на нем первообразную. Одна из первообразных задается формулой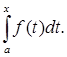

С помощью определенного интеграла можно решить такие задачи, как вычисление площади плоской фигуры, длины плоской кривой, объема тела вращения, площади поверхности тела вращения и другие. Приведем только три из перечисленных формул, которые будут нам необходимы при решении задач.

1. Площадь плоской фигуры, расположенной между прямыми ,, и графиками функций , (где , см. рис.) задается формулой:

.

Эта формула легко вытекает из определения определенного интеграла и свойства 2.

Действительно, площадь криволинейной трапеции ABCD равна: . Площадь криволинейной трапеции AEFD равна:

. Поэтому

.

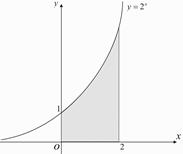Пример. Найти площадь фигуры, ограниченной линиями , ,

, . (см. рис.)

Решение.

2. Пусть функции и ее производная непрерывны на отрезке . Тогда длина графика функции на отрезке равна:

.

3. Объем тела вращения будем вычислять, опираясь на следующую теорему.

Теорема.Пусть тело образовано вращением вокруг оси Ox криволинейной трапеции 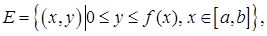где функция 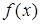непрерывна на отрезке 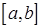. Тогда объем тела вычисляется по формуле

.

Доказательство.

Пусть есть разбиение отрезка 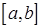с отмеченными точками 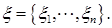Тогда объем тела можно приблизить суммой объемов цилиндров высотой 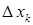и радиуса , где 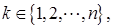то есть

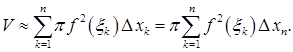(12)

Пусть - диаметр разбиения . Переходя в (12) к пределу при 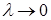в соответствии с определением, получим точную формулу

(13)

Но под знаком предела стоит интегральная сумма непрерывной на отрезке 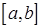функции 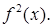Поэтому

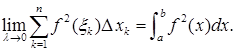
Отсюда и (13) следует формула (11). Теорема доказана.

Замечание. Если тело образовано вращением вокруг оси 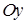криволинейной трапеции , где функция непрерывна на 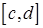, то точно также доказывается, что объем тела вычисляется по формуле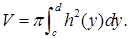

4. Экономическое приложение интеграла (см. [13]).

Если производительность труда в момент времени 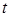задается функцией , то объем продукции, выпущенной за время 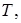равен .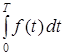

Пример.Пусть производительность труда задается функцией 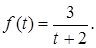Требуется найти объем 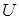продукции, произведенной за 4 часа.

Этот объем равен