Умножение квадратной матрицы на матрицу-столбец

Пример решения системы методом Гаусса

Пусть требуется решить систему трех уравнений с тремя неизвестными:

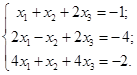
(1.1)

Будем последовательно “исключать” неизвестные. Для этого первое уравнение системы оставим без изменений, а второе и третье преобразуем:

1) ко второму уравнению прибавим первое, умноженное на –2, и приведем его к виду –3x₂ –2x₃ = –2;

2) к третьему уравнению прибавим первое, умноженное на – 4, и приведем его к виду –3x₂ – 4x₃ = 2.

В результате из второго и третьего уравнений будет исключено неизвестное x₁ и система примет вид

Второе и третье уравнения системы умножим на –1, получим

Коэффициент 1 в первом уравнении при первом неизвестном х₁называется ведущим элементом первого шага исключения.

На втором шаге первое и второе уравнения остаются без изменений, а к третьему уравнению применим тот же способ исключения переменной x₂. Ведущим элементом второго шага является коэффициент 3. К третьему уравнению прибавим второе, умноженное на –1, тогда система преобразуется к виду

(1.2)

Процесс приведения системы (1.1) к виду (1.2) называются прямым ходом метода Гаусса.

Порядок действий решения системы (1.2) называется обратным ходом. Из последнего уравнения получим х₃= –2. Подставляя это значение во второе уравнение, получим х₂ = 2. После этого первое уравнение дает х₁ = 1. Таким образом, - решение системы (1.1).

Понятие матрицы

Рассмотрим величины, входящие в систему (1.1). Набор из девяти числовых коэффициентов, стоящих в уравнениях перед неизвестными, образует таблицу чисел, которая называется матрицей:

А = .

(1.3)

Числа таблицы называются элементами матрицы. Элементы образуют строки и столбцы матрицы. Количество строк и количество столбцов образуют размерность матрицы. Матрица А имеет размерность 3´3 (“три на три”), причем первое число указывает количество строк, а второе – столбцов. Часто матрицу обозначают, указывая ее размерность А_(3´3). Так как число строк и столбцов в матрице А одинаково, матрица называется квадратной. Количество строк (и столбцов) в квадратной матрице называется ее порядком, поэтому А – матрица третьего порядка.

Правые части уравнений, также образуют таблицу чисел, т.е. матрицу:

B(3´1)= .

(1.4)

Каждая строка этой матрицы образована единственным элементом, поэтому B_(3´1)называется матрицей–столбцом, ее размерность 3´1. Набор неизвестных также можно представить как матрицу-столбец:

Х(3´1)= .

(1.5)

Умножение квадратной матрицы на матрицу-столбец

С матрицами можно производить различные операции, которые будут подробно рассмотрены в дальнейшем. Здесь же разберем только правило умножения квадратной матрицы на матрицу-столбец. По определению, результатом умножения матрицы А_(3´3) на столбец В_(3´1) является столбец D_(3´1), элементы которого равны суммам произведений элементов строк матрицы А на элементы столбца В:

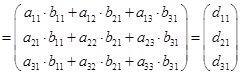
	(1.6)

Таким образом, по определению:

1) первый элемент столбца D равен сумме произведений элементов первой строки матрицы А на элементы столбца В:

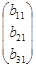
2)второй элемент столбца D равен сумме произведений элементов второй строки матрицы А на элементы столбца В:

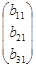
3) третий элемент столбца D равен сумме произведений элементов третьей строки матрицы А на элементы столбца В:

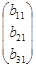
Из приведенных формул видно, что умножить матрицу 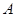на столбец В можно только в случае, если число столбцов матрицы А равно числу элементов в столбце В.

Рассмотрим еще два числовых примера умножения матрицы 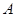_(3´3) на столбец 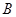_(3´1):

Пример 1.1

АВ = .

Пример 1.2

АВ = .