 |
Главная |
Задачи для самостоятельного решения. Решите системы линейных уравнений по формулам Крамера. № Система
|
из
5.00
|
Решите системы линейных уравнений по формулам Крамера.
| № | Система уравнений | Ответы |

| 
| |
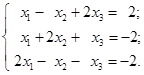
| 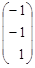
| |

| 
| |

| 
|
Обратная матрица и ее нахождение
Квадратная матрица А, определитель которой равен нулю (detA=0) называется вырожденной. Если же detA ¹ 0, тогда матрица А называется невырожденной.
Матрица А–1 называется обратной к матрице А, если выполняется соотношение
 , ,
| (1.18) |
Таким образом, произведение матрицы А на обратную к ней матрицу А–1 равно единичной матрице Е (А–1 – это обозначение матрицы, обратной к матрице А). Отметим, что умножение матрицы А на обратную обладает свойством коммутативности
 , ,
| (1.19) |
Можно доказать, что для любой невырожденной матрицы А существует единственная обратная матрица, которая находится по формуле
А–1 =  . .
| (1.20) |
В формуле (1.20) D = det(А) ¹0, элементы А11 , А12 , …– алгебраические дополнения к соответствующим элементам а11 , а12 , …матрицы А.
Пример 1.20
Найти матрицу  , обратную к матрице А=
, обратную к матрице А=  .
.
Решение
Для нахождения обратной матрицы А–1 вычислим определитель
D=  = 2+1=3
= 2+1=3
и алгебраические дополнения
А11 = 1 , А21 = 1,
А12 = –1 , А22 = 2.
После этого найдем
А–1 = 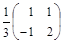 =
=  .
.
Покажем, что для найденной матрицы выполняется условие
 :
:
 .
.
Пример 1.21
Рассмотрим еще один пример нахождения обратной матрицы для матрицы третьего порядка:
А =  .
.
Решение
Вычислим определитель:
D=  =1×(–1)×0+1×(–6)×3+2×(–2)×1 – 1×(–1)×3–1×2×0–
=1×(–1)×0+1×(–6)×3+2×(–2)×1 – 1×(–1)×3–1×2×0–
– (–6)×(–2)×1= –18 – 4 + 3 –12 = –31.
Вычислим алгебраические дополнения соответствующих элементов:
А11 = 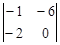 = –12; = –12;
| А21 = –  = –2; = –2;
| А31 =  = –5; = –5;
|
А12 = – 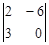 = –18; = –18;
| А22 =  = –3; = –3;
| А32 = –  = 8; = 8;
|
А13 =  = –1; = –1;
| А23 = –  = 5; = 5;
| А33 =  = –3. = –3.
|
Составим обратную матрицу:
А–1 =  =
= 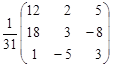 .
.
Покажем, что  .
.
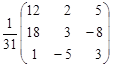 ×
×  =
=
=  =
=
=  =
=  = Е.
= Е.
Решение систем с помощью обратной матрицы
Рассмотрим систему трех линейных уравнений с тремя неизвестными (1.15):
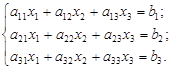
|
или в матричной записи
 . .
| (1.21) |
Если А – невырожденная матрица (det A¹0), то система (1.15) совместна и имеет единственное решение. Умножая обе части равенства (1.21) слева на матрицу А–1, обратную к матрице А, получаем
| Х = А–1 B. | (1.22) |
Пример 1.22
Решить систему уравнений с помощью обратной матрицы:

Решение
А =  .
.
Обратная матрица найдена в примере 1.21 и имеет вид
А–1 = 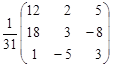 .
.
По формуле (1.22) получаем
Х = 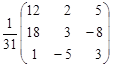 ×
× 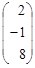 =
= 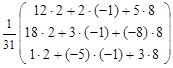 =
=
=  =
=  .
.
Таким образом, решение системы: (2; –1; 1).
Покажем, что если D= detA¹0, то формулы Крамера (1.16) могут быть получены из формулы (1.21). Действительно, из выражений (1.22) и (1.20) и (1.14) последовательно получаем
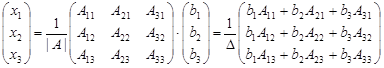 .
.
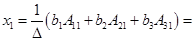


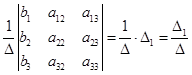 ;
;
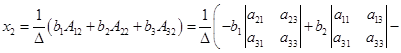

 ;
;



 .
.
Задачи для самостоятельного решения
Решите системы линейных уравнений с помощью обратной матрицы.
| № | А | В | Х (ответы) |
| 1) | 
| 
| 
|
| 2) | 
| 
| 
|
| 3) | 
| 
| 
|
| 4) | 
| 
| 
|
| 5) | 
| 
| 
|
| 6) | 
| 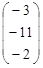
| 
|
.
.
|
из
5.00
|
Обсуждение в статье: Задачи для самостоятельного решения. Решите системы линейных уравнений по формулам Крамера. № Система |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

