Вычисление двойного интеграла

Несобственные интегралы I и II рода

 

Понятие определенного интеграла было введено для функций, заданных на интервале [a; b]. Однако существуют понятия интеграла на случай функций, определенных на неограниченных интервалах.

Пусть функция определена на бесконечном интервале [a; ¥) и интегрируема на любом интервале [a; b], где b < ¥.

Несобственным интегралом I рода функции f(x) на интервале [a; ¥) называется предел

= (6)

Если предел в левой части равенства (6) является конечным числом, то интеграл называется сходящимся, если этого предела не существует или он равен ¥, то говорят, что интеграл расходится.

 

Пример 6. Вычислить несобственный интеграл или установить его расходимость.

Решение

Имеем

| | =

 

Тест 6. Вычислить несобственный интеграл или установить его расходимость:

1) расходится;

2)

3) 1;

4)

5) 2.

 

При введении понятия определенного интеграла предполагалось, что подынтегральная функция на [a; b] является ограниченной. Тем не менее существует обобщение понятия определенного интеграла и на случаи, когда нарушается требование ограниченности подынтегральной функции на [a; b].

Предположим, что f(x) является ограниченной и интегрируемой на любом отрезке [a + e; b], 0 < e < b – a, но неограниченной в любой окрестности точки а. В таком случае точка а называется особой точкой.

Несобственным интегралом II рода функции f(x) на отрезке [a; b] называется предел

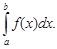= (7)

Если предел в левой части равенства (7) существует и является конечным числом, то интеграл называется сходящимся. В противном случае он называется расходящимся.

 

Пример 7. Вычислить несобственный интеграл или установить его расходимость.

Решение

Имеем

| =

Делаем вывод, что данный несобственный интеграл расходится.

 

Тест 7.Вычислить несобственный интеграл или установить его расходимость:

1) расходится;

2)

3) 1;

4)

5) 2.

 

Приближенные методы вычисления
определенных интегралов

 

Существует много формул приближенного вычисления определенных интегралов. Приведем наиболее простую из них – формулу трапеций.

Пусть в интеграле функция f(x) непрерывна на отрезке [a; b]. Разобьем отрезок [a; b] на n равных частей точками = 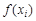– значение функции = 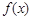в точке Тогда имеет место так называемая формула трапеций

(8)

 

Пример 8. Вычислить приближенно определенный интеграл применив формулу трапеций, взяв n = 3.

Решение

Находим шаг h: Получаем: x₀ = 1, x₁ = 2, х₂ = 3, х₄ = 4. Тогда соответствующими значениями функции y₀ = 1, Подставляя эти значения в формулу (8), получим

 

Тест 8. Вычислить приближенно определенный интеграл применив формулу трапеций, взяв n = 4:

1)

2) 2;

3)

4)

5)

 

Ответы на тестовые задания

 

Номер теста
Правильный ответ

 

 

Кратные интегралы

 

Множество точек называется связным, если любые две из них можно соединить линией, все точки которой принадлежат данному множеству.

Под геометрической фигурой Ф будем понимать одно из следующих связных (включая границу) множеств точек:

1) линия L в R²или R³, в частности отрезок [a; b] координатной оси;

2) плоская область D в R² (рисунок 52);

3) поверхность Q в R³ (рисунок 53);

4) пространственная область V в R³, ограниченная замкнутой поверхностью, − тело в пространстве (рисунок 53).

Определение. Диаметром d фигуры Ф называется максимальное расстояние между двумя ее точками.

 

Пример 1. Диаметр параллелограмма − длина большей диагонали.

В дальнейшем будем рассматривать фигуры конечного диаметра (ограниченные).

Определение. Подмерой фигуры Ф будем понимать: для отрезка [a; b] − его длину |[a; b]|, для линии L − ее длину l, для плоской области D и поверхности Q − их площади s и q соответственно, для пространственной области V − объем v соответствующего тела.

Рассмотрим фигуру Ф, мера которой μ, и определенную на ней непрерывную скалярную функцию f(P), P Î Ф. Осуществим построение, геометрическая интерпретация которого применительна к плоской области D. Выбранная в качестве конкретного примера фигура Ф дана на рисунках 52 и 53.

Для этого выполним следующие действия:

1. Разобьем Ф произвольным образом на n элементарных фигур ΔФ_i с мерами Δμ_i, i = 1, 2, ¼, n.

2. На каждой элементарной фигуре выберем произвольную точку P_i ΔФ_i и вычислим значения f(P_i) функции в этих точках.

3. Найдем произведения f(P_i )Δμ_i, i = 1, 2, ¼, n.

4. Составим сумму

S_n = 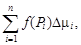(1)

которую будем называть n-й интегральной суммой для функции f(P) по фигуре Ф.

5. Перейдем к пределу в сумме (1) при условии, что наибольший из диаметров λ элементарных фигур ΔФ_i стремится к 0

S_n =

Очевидно, что для данной фигуры Ф и выбранного n можно составить сколько угодно интегральных сумм, зависящих от разбиения фигуры Ф и выбора точек P_i ΔФ_i.

 

 

У

D

Z

Рисунок 52 Рисунок 53

 

Определение. Предел n-й интегральной суммы (1) для данной функции f(P) и фигуры Ф при условии, что каждая из элементарных фигур стягивается в точку (λ→0), если он существует, конечен и не зависит от способа построения интегральной суммы, называетсяинтегралом по фигуре Ф от скалярной функции f(P) и обозначается

= (2)

Теорема. Если на связной, ограниченной и содержащей граничные точки фигуре Ф скалярная функция f(P) непрерывна, то интеграл по фигуре Ф от этой функции существует.

 

Частные случаи интегралов по фигуре (кратных интегралов)

 

Определенный интеграл

 

Пусть Ф – отрезок [a; b] координатной оси Ох. Мерой μ отрезка
[a; b] является его длина, μ=|[a; b]|= b – a. Обозначим также Δμ_i = Δx_i и λ = max{Δx_i}, i = 1, 2, …, n. Тогда интегральная сумма (1) для функции f(P)= f(x) примет вид

S_n = =

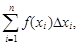
и ее предел, если он существует, называется определенным интегралом (однократным интегралом)и обозначается

= =

где Ф = [a; b] – отрезок интегрирования;

x – переменная интегрирования;

a и b – соответственно нижний и верхний пределы интегрирования.

 

Двойной интеграл

 

Пусть фигура Ф – плоская область D, которой принадлежит ее граница (кривая L). Мерой μ такой фигуры является его площадь s,
т. е. μ = s. Обозначим также Δμ_i = Δs_iи λ = max{Δs_i}, i = 1, 2, ¼, n. Тогда интегральная сумма (1) для функции z = f(P) = f(x; y) примет вид

S_n = =

и ее предел, если он существует, называется двойным интегралом отфункции z = f(x; y) по области D и обозначается

= = (3)

где D – область интегрирования;

x, y – переменные интегрирования;

dxdy – дифференциал площади плоской области D.

 

Тройной интеграл

 

Пусть фигура Ф – область V Ì R³, ограниченная замкнутой поверхностью. Мерой μ такой фигуры является его объем v, т. е. μ = v. Обозначим также Δμ_i = Δv_iи λ = max{Δv_i}, i = 1, 2, …, n. Тогда интегральная сумма (1) для функции f(P) = f(x; y; z), P Î V, примет вид

S_n = =

и ее предел, если он существует, называется тройным интегралом от функции f(x; y; z) по пространственной области D и обозначается

= =

где V – область интегрирования;

x, y, z – переменные интегрирования;

dxdydz – дифференциал объема пространственной области V.

 

Свойства интегралов по фигуре (кратных интегралов). Свойства интегралов по фигуре аналогичны свойствам однократных определенных интегралов как частным случаям интеграла по фигуре.

Геометрический смысл двойного интеграла. Пусть функция
z = f(P) = f(x; y) принимает в области D только положительные значения. Тогда двойной интеграл численно равен объему V вертикального цилиндрического тела, построенного на основании D и ограниченного сверху соответствующим куском поверхности z = f(x; y) (рисунки 53 и 54).

Рисунок 54

Вычисление двойного интеграла

1. Пусть функция f(x; y) непрерывна в области D. Если D – прямоугольник, то при вычислении двойного интеграла имеет место формула

(4)

которая показывает, что порядок интегрирования можно менять.

Интеграл (4) представляет собой объем тела, ограниченного снизу прямоугольником P, сбоку – боковыми гранями прямой призмы, построенной на этом прямоугольнике, а сверху – той частью поверхности, которая вырезана этой призмой (рисунок 55).

 

 

Рисунок 55

 

2. Если функция f(x; y) непрерывна на множестве D = {(x; y): a ≤ x ≤ b, y₁(x) ≤ y ≤ y₂(x)},где y₁(x)и y₂(x) непрерывны на отрезке [a; b] и y₁(x)≤
≤ y₂(x) на [a; b] (область D правильная в направлении оси OY, т. е. любая прямая, параллельная оси OY, пересекает область D не более чем в двух точках) (рисунок 56), то верно равенство

(5)

Правая часть в формуле (4) называется повторным интегралом, a и b − его внешними пределами (они всегда постоянны), y₁(x) и y₂(x) − внутренними пределами интегрирования (они могут быть переменными и постоянными). Вначале вычисляется внутренний интеграл, при этом вторая переменная (в данном случае x), соответствующая внешнему интегралу, считается постоянной, а затем – внешний интеграл с последующим применением формулы Ньютона-Лейбница.

3. Если функция f(x; y) непрерывна в области D (рисунок 57),
D = {(x; y): c ≤ y ≤ d, x₁(y) ≤ x ≤ x₂(y), где функции x₁(y) и x₂(y) непрерывны на сегменте [c; d] и x₁(y)≤ x₂(y)на [c; d] (область D правильнаяв направлении оси OX, т. е. любая прямая, параллельная оси OX, пересекает область D не более чем в двух точках), то верно равенство

(6)

 

 

Рисунок 56 Рисунок 57

 

4. Если область D такова (рисунок 52), что к ней применима и формула (5), и формула (6), то

Это равенство используется для перемены порядка интегрирования в повторном интеграле.

Области более сложного вида следует разбить на части, к которым применима формула (5) или (6).