 |
Главная |
Бесконечно малые функции и основные теоремы о них
|
из
5.00
|
Если  , то функция f называется бесконечно малой при x → x0
, то функция f называется бесконечно малой при x → x0
Теорема 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
▼Пусть α(х) и ß(х) — две б.м. функции при х→хо. Это значит, что lim α(х)=0, при х→х0 т.е. для любого ε>0, а значит, и ε/2>0 найдется число δ1>0 такое, что для всех х, удовлетворяющих неравенству 0<|х-х0|<δ1, выполняется неравенство

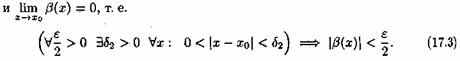
Пусть δ — наименьшее из чисел δ1 и δ2.Тогда для всех х, удовлетворяющих неравенству 0<|х-хо|<δ, выполняются оба неравенства (17.2) и (17.3). Следовательно, имеет место соотношение

Таким образом

Аналогично проводится доказательство для любого конечного числа б.м. функций.
Теорема 2 Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
▼ Пусть функция ƒ(х) ограничена при х→хо. Тогда существует такое число М>0, что

для всех х из δ1-окрестности точки хо. И пусть α(х)—б.м.ф. при х→x0. Тогда для любого ε >0, а значит, иε /М> 0 найдется такое число δ2>О, что при всех х, удовлетворяющих неравенству 0<|х-хо|<δ2, выполняется неравенство

Обозначим через δ наименьшее из чисел δ1 и δ2. Тогда для всех х, удовлетворяющих неравенству 0<|х-хо|<δ, выполняются оба неравенства (17.4) и (17.5). Следовательно, |ƒ(х)-α(х)|=|ƒ(х)|-|а(х)|<ε.
А это означает, что произведение ƒ(х)•α(х) при х→х0 есть бесконечно малая функция.▲
Следствие 17.1. Так как всякая б.м.ф. ограничена, то из теоремы (17.2) вытекает: произведение двух б.м.ф. есть функция бесконечно малая.
Следствие 17.2. Произведение б.м.ф. на число есть функция бесконечно малая.
Теорема 17.3. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.

Связь между функцией, ее пределом и бесконечно малой функцией
Теорема 5. Если функция ƒ(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции α(х), т. е. если limƒ(х)=А, при Х→Хо то ƒ(х)=А+а(х).
▼ Пусть 
Следовательно,

т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).▲
Теорема 6(обратная). Если функцию ƒ(х) можно представить в виде суммы числа А и бесконечно малой функции α(х), то число А является пределом функции ƒ(х), т. е. если ƒ(х)=А+α(х), то lim ƒ(х)=А при Х→Хо

Бесконечно большая функция.
Функция f(x) называется бесконечно большой функцией в точке а (или просто бесконечно большой), если её предел стремится к бесконечности.
Между бесконечно малыми и бесконечно большими функциями существует та же связь, что и между соответствующими последовательностями, т.е. если α(х) — бесконечно малая функция при х  а, то f(x) = 1/α(х) — бесконечно большая функция, и наоборот.
а, то f(x) = 1/α(х) — бесконечно большая функция, и наоборот.
|
из
5.00
|
Обсуждение в статье: Бесконечно малые функции и основные теоремы о них |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

